Dit bericht is geplaatst op dinsdag 26 december 2006 om 15:00 in categorieën Algemeen, Geschiedenis. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Het vierkleurenprobleem
In Algemeen,Geschiedenis, door wiskundemeisjes
(Speciaal voor de kerstvakantie: een lang stuk over het vierkleurenprobleem dat ik schreef voor de site van Reken mee met abc (die binnenkort online komt.))
In 1852 was Francis Guthrie bezig om een kaart van de Engelse counties netjes in te kleuren. Netjes betekent in dit geval dat hij wilde zorgen dat elke twee aan elkaar grenzende counties verschillende kleuren hadden, zodat duidelijk was waar counties begonnen en eindigden. Guthrie ontdekte dat hij maar vier verschillende kleuren nodig had. Hij vroeg zich af of je misschien voor elke landkaart genoeg zou hebben aan vier kleuren. Daarmee was het befaamde vierkleurenprobleem geboren.
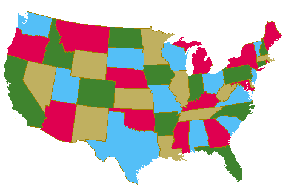
De kaart met de verschillende staten van Amerika is ook met vier kleuren in te kleuren. Guthrie vermoedde dat dit voor elke kaart zou lukken.
Guthrie vroeg aan de bekende wiskundige De Morgan hoe hij zijn vermoeden moest bewijzen. De Morgan had geen flauw idee, maar werd gegrepen door het probleem. Hij stuurde de vraag nog dezelfde dag naar de beroemde Hamilton met de opmerking "Als jij met een of ander slim voorbeeld komt waardoor ik een dom dier lijk, dan zal ik voortaan moeten zwijgen als de sfinx...". Gelukkig voor hem kwam Hamilton niet met een slim voorbeeld van een landkaart waarvoor vijf kleuren nodig waren of met een eenvoudig bewijs. Integendeel: Hamilton schreef enkele dagen later terug: "Het is niet erg waarschijnlijk dat ik binnenkort iets zal proberen te doen met dat viertal kleuren van jou". De Morgan bleef daarna bij wiskundigen aandringen dat ze naar een oplossing moesten zoeken.
Het duurde een tijd voor er resultaten geboekt werden. De eerste die het lukte om iets te bewijzen, was Arthur Cayley in 1878. Hij bewees dat het genoeg was om alleen te kijken naar landkaarten waar steeds precies drie landen in een punt bij elkaar komen. Het lukte hem niet om het probleem verder op te lossen; in zijn artikel gaf hij ook aan waar de moeilijkheden van een bewijs lagen.
Bewijzen en tegenvoorbeelden met een luchtje
Vlak daarna beweerden twee mensen dat zij het vermoeden van Cuthrie bewezen hadden. De advocaat Alfred Kempe publiceerde in 1879 zijn bewijs in Nature. Kempe had trouwens ook wiskunde gestudeerd, bij Cayley in Cambridge. Een jaar later kwam wiskundige Peter Tait met een ander bewijs. Tien jaar lang leefden mensen in de gelukzalige veronderstelling dat het vierkleurenprobleem was opgelost. Vooral Kempe ontving veel eer voor zijn werk; hij werd bijvoorbeeld gekozen tot lid van de Royal Society - de Britse academie voor wetenschappen. Maar in 1890 vond Percy Heawood een cruciale fout in het bewijs van Kempe. En tot overmaat van ramp bleek een jaar later ook het bewijs van Tait niet te kloppen. Zo waren de wiskundigen weer terug bij af. Kempes methode bleek heel nuttig voor verder onderzoek, maar het was natuurlijk een grote tegenvaller dat zijn bewijs niet waterdicht was. Wie meer wil weten over zijn bewijs en de fout daarin, kan meer hierover lezen in dit artikel uit Pythagoras: Vier kleuren is voldoende', zegt de computer.
Er was een klein lichtpuntje: dezelfde Heawood die de fout in het bewijs van Kempe ontdekte, kon met behulp van de ideeen van Kempe wel bewijzen dat je voor elke kaart genoeg had aan vijf kleuren. Hij besteedde maar liefst zestig jaar van zijn leven aan het vierkleurenprobleem, maar kwam niet tot een algemeen bewijs dat je ook aan vier kleuren genoeg had. Daarna werden nog verschillende ontdekkingen gedaan; zo bewees Franklin in 1922 dat het vermoeden waar was voor alle kaarten met hooguit 25 landen. Het duurde echter tot 1976 tot Kenneth Appel en Wolfgang Haken met een algemeen bewijs kwamen.
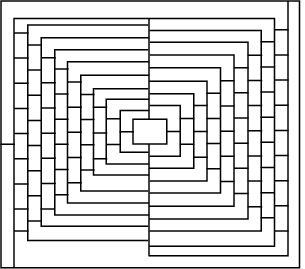
In 1975 haalde Martin Gardner een mooie 1 aprilgrap uit, door te beweren dat de kaart hierboven niet met vier kleuren kon worden ingekleurd. Dit plaatje zou dus bewijzen dat de vierkleurenstelling niet waar is. Wie echter goed puzzelt, heeft aan vier kleuren genoeg om de 110 'landen' op deze kaart netjes te kleuren.
Het bewijs?
Appel en Wolfgang gebruikten in hun bewijs ideeen die eerder bij Kempe en anderen voorkwamen. Omdat het onmogelijk is om alle landkaarten te bekijken, brachten ze het probleem terug tot een eindig aantal gevallen. Ze gebruikten hierbij zogenaamde onvermijdelijke situaties. Dit is een verzameling van situaties (landen die op een bepaalde manier aan elkaar grenzen), waarvan elke willekeurige landkaart er minstens een moet bevatten. Deze verzameling is behoorlijk groot, er zaten ongeveer 1500 verschillende gevallen in. Het tweede idee dat Appel en Wolfgang gebruikten is dat sommige kaarten te vereenvoudigen zijn. Als zo'n kaart niet met vier kleuren te kleuren is, dan is er een kleiner deel van die kaart dat ook al niet met vier kleuren te doen is.
Deze twee ideeen met elkaar gecombineerd leverden een bewijs op, waar nog wel een heleboel rekenwerk voor nodig was. Uiteindelijk gebruikten Appel en Wolfgang een computer om alle mogelijke gevallen door te rekenen; dit kostte meer dan 50 dagen rekentijd. Daarnaast moesten ze ook nog zo'n 10.000 situaties met de hand uitwerken. Sommige wiskundigen zijn niet gelukkig met hun bewijs, omdat het computerdeel niet door mensen na te kijken is. Ook hebben sommigen principiele bezwaren tegen het gebruik van computers bij bewijzen, omdat er daarbij fouten kunnen worden gemaakt. Hoe weet je zeker dat de computer doet wat de programmeur wil? Voorstanders van computerbewijzen voeren aan dat ook mensen fouten maken in het nakijken van bewijzen, zoals we honderd jaar eerder zagen bij de bewijzen van Kempe en Tait.
In de jaren negentig kwamen Neil Robertson, Daniel Sanders, Paul Seymour en Robin Thomas met een nieuw, eenvoudiger bewijs voor de vierkleurenstelling, waarbij maar 633 verschillende onvermijdelijke situaties bekeken hoefden te worden. Ook zorgden ze ervoor dat het aantal berekeningen per situatie sterk verminderde. Er was nog steeds een computer nodig om alle mogelijkheden door te rekenen. In 2004 herschreef George Gonthier het bewijs van Robertson (en de rest), zodat hij het computerbewijs kon nakijken met zijn programma Coq. Dit is een computerprogamma dat speciaal gemaakt is om wiskundige bewijzen te controleren. Gonthier bevestigde, dat het bewijs van Robertson (en de rest) klopt. Nu moeten wiskundigen alleen nog maar het programma Coq vertrouwen om te kunnen geloven dat het vierkleurenprobleem echt is opgelost...
(Ionica)
 Internetbureau Rotterdam
Internetbureau Rotterdam 
