Wiskundemeisjes

Deze column verscheen afgelopen weekend in de Volkskrant.

Beste winkeliers van Nederland,

De benzineprijzen zijn naar recordhoogte gestegen, luxe-artikelen werden nog snel ingeslagen, en de consument schijnt per 1 oktober de hand op de knip te houden: per afgelopen maandag werd het hoge btw-tarief, de btw op luxe producten en diensten, verhoogd van 19 naar 21 procent. Geen mooi vooruitzicht voor uw inkomsten! Daar moest u iets op verzinnen.

Dus haalde u eind september nog snel even de aloude btw-kortingsacties van stal, nu de korting die u moest geven nog enigszins te overzien was. Tijdens dergelijke acties hoeven uw klanten tijdelijk geen btw te betalen. Niet echt natuurlijk, want op elke transactie wordt gewoon btw geheven, maar het bedrag dat normaal gesproken de btw zou uitmaken wordt nu omgezet in een korting.

Zo las ik bijvoorbeeld op een autoverkoopwebsite: “Citroën neemt in september de btw van de C4 en de C4 Picasso voor haar rekening. Dat betekent dat je een korting van 19 procent op de nieuwprijs krijgt.” Hetzelfde geldt voor de 21 procent korting die de Formido begin oktober nog belooft op een product naar keuze (“21% btw? Daar doen we (nog) niet aan mee! Nu 21% korting!”).

19 Procent korting, dat is nogal wat! Het is zelfs méér dan de btw die u beweert aan uw klanten cadeau te doen. Reken maar na. We bekijken een auto die – even voor het gemak – 10.000 euro kost exclusief btw. Daar kwam in september dan nog 19 procent btw bij, oftewel 1.900 euro, zodat de kostprijs normaal gesproken 11.900 euro zou worden.

Nu gaf u 19 procent korting. Dat is 0,19 x 11.900 = 2.261 euro. Veel meer dus dan de 1.900 euro die aan btw betaald zou moeten worden. De consument hoefde nog maar 9.639 euro te betalen, terwijl de auto exclusief btw 10.000 euro kost. Hoe dat komt? Nou, het btw-percentage van 19 procent is een percentage van de kale prijs zonder btw, terwijl de korting van 19 procent een percentage is van de hogere totaalprijs inclusief btw.

Het is dus eigenlijk helemaal niet verstandig te stunten met 19 of 21 procent korting, zoals de Citroënverkoper respectievelijk de Formido doen, want dat kost u meer dan alleen de btw. Maar de meesten van u begrepen dit best.

De Mediamarkt bijvoorbeeld, die stuntte met de slogan ‘19% btw Weg ermee!’ Hoeveel korting gaf u dan eigenlijk, als u de btw weghaalde? We kijken weer even naar die auto. De btw bedroeg 1.900 euro op het totaalbedrag van 11.900 euro. Dat is dus 1.900/11.900 x 100 procent, oftewel ongeveer 16 procent, van de totaalprijs. Om de btw te compenseren, hoefde u dus maar 16 procent korting te geven.

Slim van u dus, die slogan ‘19% btw Weg ermee!’. Helemaal correct, en de 19 procent bleef hangen in mijn hoofd. U klonk dus erg gul en intussen gaf u gewoon de 16 procent korting die het btw-bedrag bedroeg. En klanten die boos komen klagen dat ze geen 19 procent korting hebben gekregen, maar slechts 16, kunt u doorverwijzen naar de vragensectie op uw actiesite, waar het bovenstaande verhaal haarfijn wordt uitgelegd. Mijn welgemeende complimenten!

Met oplettende groeten,
Jeanine

Deze column verscheen gisteren in de Volkskrant.

Geachte Dr. Jasper Verguts,

Als gynaecoloog ziet u natuurlijk heel wat baarmoeders. Ik las in The Guardian dat u op het idee bent gekomen om tijdens echo’s die baarmoeders te meten. U mat 5000 baarmoeders op en toen ontdekte u iets opvallends: in de vruchtbaarste periode van een vrouwenleven ligt de verhouding tussen hoogte en breedte van de baarmoeder rond de 1,6. En toen dacht u natuurlijk aan de gulden snede, de beroemde verhouding die alles mooi en goed maakt. U concludeerde dat de gulden-snedeverhouding blijkbaar ook de optimaalste baarmoederverhouding is.

U weet natuurlijk wel wat die beroemde gulden snede precies is. Als je een strook papier in twee stukken verdeelt met lengtes a en b (waarbij a het langste is), en de verhouding a staat tot b (dus het langste ten opzichte van het kortste) gelijk is aan de verhouding a + b staat tot a (dus de hele strook ten opzichte van het langste stuk), dan is die verhouding gelijk aan , ongeveer 1,618.

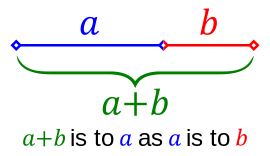
Binnen de wiskunde duikt dit getal inderdaad op onverwachte plekken op, bijvoorbeeld in de lengteverhoudingen in een pentagram, en ook in de beroemde getallenrij van Fibonacci. Die begint als 1, 1, 2, 3, 5, 8, 13, …, en je krijgt het volgende getal steeds door de twee voorgaande getallen bij elkaar op te tellen. De verhouding tussen een getal en zijn voorganger kruipt, naarmate de getallen verder in de rij staan, steeds dichter naar de gulden snede toe. Dat is wiskundig te bewijzen.

Maar u signaleert de verhouding nu in de baarmoeder. Net zoals die door vele anderen gezocht is in vingerkootjes, muziek van Bach, het Parthenon, piramides, noem maar op. Er wordt vaak beweerd dat de gulden snede een verhouding is die mensen prettig vinden. Daar is echter geen bewijs voor. En als esthetisch principe is de gulden snede pas in de negentiende eeuw gesignaleerd, dus in oude kunst en gebouwen zal hij niet moedwillig gebruikt zijn.

Wat nog vervelender is: door alleen een meting kun je nooit bewijzen dat iets precies de gulden snede is. Zelfs als je heel precies 1,618 gemeten hebt, klopt het een paar decimalen verder niet meer helemaal, en uw 1,6 is maar op één decimaal nauwkeurig. Maar dat is eigenlijk niet eens belangrijk.

Als u goed rondkijkt, ziet u dat veel dingen om ons heen niet extreem lang of smal zijn, wat als gevolg heeft dat de verhoudingen die we zien vaak tussen de 1 en de 2 zullen liggen. Iets in de buurt van de 1,6 is dus niet raar. Net als 1,8 of 1,25. Je kunt bij elke verhouding dingen vinden die er in de buurt zitten, als je er maar naar zoekt.

De baarmoederverhouding waar het om draait is in het begin van het leven ongeveer gelijk aan 2, en bij oude vrouwen 1,46. Qua orde van grootte zitten we dus sowieso al in de buurt. En als iets van 2 verandert in 1,46, ja, dan ligt daartussenin natuurlijk wel een keer ongeveer 1,6, dat is nogal wiedes! Uw verband met de gulden snede lijkt mij nogal vergezocht.

Met hartelijke groeten,
Jeanine

Deze column verscheen gisteren in de Volkskrant.

In onze wiskundekantine zei een professor van een niet nader te noemen ander vakgebied eens verbaasd: “Wat zijn de mensen hier aardig tegen elkaar!” Dat klopt: wiskundigen maken niet zo vaak ruzie met elkaar. Niet om inhoudelijke kwesties, in ieder geval. Als iemand iets beweert wat niet klopt, kan een ander daar namelijk een sluitend argument tegen inbrengen. En de een accepteert dat dan, neemt zijn verlies, en is in het beste geval zelfs blij dat hij iets geleerd heeft. Er is geen richtingenstrijd, de onenigheden gaan hoogstens over welke soorten vragen en argumenten het mooist of interessantst zijn.

Maar over erkenning en prioriteit zijn in de geschiedenis van de wiskunde wel ruzies uitgevochten. Een mooi verhaal is dat van de ontdekking van de formule voor de oplossingen van de derdegraads vergelijking in het Italië van de zestiende eeuw.

U kent de abc-formule wel: de oplossingen van de algemene kwadratische vergelijking worden gegeven door . Het is een voor de hand liggende vraag of zo’n formule ook bestaat voor de derdegraads vergelijking , en het antwoord is ja. Wat die formule precies is, is nu niet belangrijk, hij ziet er nogal ingewikkeld uit.

De eerste die één type derdegraads vergelijking algemeen kon oplossen was Scipione del Ferro, rond 1515. Zo’n ontdekking ga je natuurlijk van de daken schreeuwen! Nee. Ook toen speelden economische motieven een rol: je moest geld verdienen, bijvoorbeeld door een mecenas te vinden. Dat lukte beter als jij iets kon dat niemand anders kon, en dat wilde je dan graag zo houden. Om te bewijzen dat je iets bijzonders kon, daagde je iemand uit met een set problemen die je zelf had opgelost, in de hoop dat de ander dat niet zou kunnen. En als tegenactie gaf die persoon jou ook problemen op. Een wiskundeduel, zeg maar.

Del Ferro deed dat niet, maar hij gaf de oplossing voor zijn dood wel door aan onder andere zijn leerling Fiore. Die hoorde op een bepaald moment dat Niccolò Tartaglia (dit was zijn bijnaam, “tartaglia” betekent “stotteraar”) opschepte dat hij derdegraads vergelijkingen kon oplossen. Fiore daagde hem natuurlijk uit. Fiore kon echter maar één type vergelijking oplossen, en Tartaglia slaagde erin dat type ook te kraken. Hij kon Fiore vervolgens uitdagingen terugsturen die die niet kon oplossen. Dus Tartaglia won.

Ronde twee. Gerolamo Cardano hoorde van deze wedstrijd en probeerde Tartaglia over te halen zijn oplossing te delen. Tartaglia weigerde natuurlijk. Maar nadat Cardano eeuwige geheimhouding beloofd had, naast verleidelijke uitnodigingen voor introducties bij het Milanese hof, ging hij overstag!

Cardano breidde de oplossing uit, en zijn leerling Ferrari vond zelfs de formule voor de vierdegraads vergelijking. En Tartaglia publiceerde maar niets. Toen Cardano er achter kwam dat Del Ferro ook al een gedeeltelijke oplossing had gehad, voelde hij zich niet meer verplicht tot geheimhouding en in 1545 publiceerde hij de oplossing (waarbij hij Tartaglia wel noemde). Tartaglia was woedend en een strijd vol beledigingen en uitdagingen volgde. Hij daagde Ferrari uit, en… verloor. De formule staat nu bekend als de “formule van Cardano”. Dus zijn eedbreuk heeft hem wel mooi eeuwige roem bezorgd.

Deze column verschijnt vandaag in de Volkskrant.

Op allerlei onverwachte plekken kom je wiskunde tegen, zelfs op vakantie. Zo was ik laatst in Barcelona en, zoals het goede toeristen betaamt, gingen we de Sagrada Familia bezichtigen.

Al sinds 1882 wordt er aan de Sagrada Familia gebouwd, in 1883 kreeg architect Antoni Gaudí (1852 – 1926) de leiding. Gaudí is ook verantwoordelijk voor Park Güell (en indirect dus ook voor al die gemozaïekte salamanders die je in Barcelona op elke straathoek kunt aanschaffen).

Gaudí werkte tot zijn dood fanatiek aan de Sagrada (hij ging zelfs op de bouwplaats wonen!) en maakte een heleboel maquettes en schetsen. Helaas is veel verloren gegaan door een brand tijdens de Spaanse burgeroorlog, dus moesten de latere architecten reconstrueren wat Gaudí van plan was, en de rest zelf aanvullen met nieuwe plannen.

Een hoog gebouw met veel torens en ingewikkelde gewelven bouwen, is niet gemakkelijk. Hoe zorg je er bijvoorbeeld voor dat de pilaren en gewelven stabiel staan?

Gaudí verdiepte zich onder andere in de kettinglijn. Een kettinglijn is de vorm die een ketting aanneemt als je hem vrij laat hangen en alleen aan de uiteindes vasthoudt. Op het moment dat de ketting stilhangt, is een evenwichtstoestand ontstaan tussen de drie krachten die op elke schakel werken: de zwaartekracht en de twee spankrachten (links en rechts). Op dat evenwichtsmoment zijn er in die ketting alleen trekkrachten aanwezig in de richting van de ketting zelf.

Als je zo’n kettinglijn op de kop zou zetten, zouden alle drukkrachten dus ook precies in de richting van de boog zelf lopen, waardoor er niet van bijvoorbeeld opzij aan de boog getrokken wordt en hij dus heel stevig staat. De kettinglijn is al bekend sinds de zeventiende eeuw (onder andere Christiaan Huygens en Galileo Galilei hielden zich ermee bezig).

Maar een gewelf is ingewikkelder dan een poort of boog, die in principe maar twee-dimensionaal zijn. Voor een boog kun je nog redelijk eenvoudig controleren of hij in evenwicht is: je kijkt of je een kettinglijn kunt maken die (op de kop) dezelfde vorm heeft als de boog die je in gedachten had.

Voor het ontwerpen van een gewelf moet je drie dimensies gebruiken. Je kunt daar een beetje mee smokkelen door naar dwarsdoorsnedes te kijken, maar echt drie-dimensionaal aan krachten rekenen is ingewikkeld. Gaudí gebruikte verschillende methodes, maar de tofste vind ik zijn hangende modellen. (Die gebruikte hij niet voor de Sagrada trouwens, maar voor een ander kerkontwerp.) Gaudí maakte van een heleboel touwtjes met gewichtjes eraan een op zijn kop hangend kerkgewelf. Oftewel: hij ontwierp het gewelf direct op stabiliteit. En door te variëren met touwtjes en gewichtjes kon hij het ontwerp meer naar zijn zin maken.

Behalve een replica van een indrukwekkend hangend model is in het museum bij de Sagrada Familia nog meer wiskunde te zien: Gaudí gebruikte kegelsnedes zoals parabolen en hyperbolen in zijn ontwerpen, en op de Sagrada staat ook nog eens een magisch getallenvierkant, waarin de som in alle rijen, kolommen, diagonalen en nog wat van die dingen steeds weer 33 is, de leeftijd van Jezus toen hij werd gekruisigd.

Al met al een aanrader voor de wiskundige toerist!

Deze column verscheen vandaag in de Volkskrant.

In onze vorige column kon u lezen dat er in Hilberts hotel, een hotel met oneindig veel kamers die genummerd zijn als 1, 2, 3, …, altijd plaats lijkt te zijn. Zelfs als elke kamer bezet is, kan een verdwaalde laatkomer toch een plekje krijgen: iedereen schuift een kamer op. En ook grotere groepen, soms zelfs oneindig groot, pasten er toch steeds weer in.

Dit gaf het gevoel dat alle oneindigheden in Hilberts hotel pasten. Maar wat betekent passen of “even groot” precies? Wiskundigen noemen groepen dingen “even groot” als je ze één op één aan elkaar kunt koppelen. Bijvoorbeeld: er zijn evenveel positieve gehele getallen (1, 2, 3, …) als positieve even getallen (2, 4, 6, …), want je kunt elk getal koppelen aan het dubbele: 1 aan 2, 2 aan 4, 3 aan 6, enzovoorts.

Dit type oneindig heet “aftelbaar”. Er is een duidelijke nummer 1 aan te wijzen, een nummer 2, enzovoorts. Je bent nooit klaar met aftellen, want de verzameling is oneindig, maar je kunt ze op een rijtje zetten, net als 2, 4, 6, … en de kamers in Hilberts hotel. Ook de verzameling van breuken, al lijkt die veel groter, is aftelbaar. Maar niet alle getallen zijn breuken: en zijn beroemde voorbeelden.

De verzameling van alle getallen tussen 0 en 1 is niet aftelbaar. Het bewijs is bijzonder elegant, maar vereist wel enig hersenwerk.

Getallen tussen 0 en 1 hebben een (oneindig lange) decimale ontwikkeling, bijvoorbeeld: of of .

Stel dat je wel een (oneindig lange) lijst kunt opstellen waar ze allemaal op staan. Wat blijkt? Hoe die lijst er ook uitziet, je kunt altijd een nieuw getal tussen 0 en 1 construeren dat niet op de lijst staat. Dat doe je als volgt. We beginnen met 0 en de komma. Nu gaan we de eerste decimaal van het nieuwe getal als volgt bepalen: als de eerste decimaal van het eerste getal op de lijst geen 2 is, kiezen we een 2, en als het wel een 2 was kiezen we een 1.

Nu verschilt de eerste decimaal van ons nieuwe getal van de eerste decimaal van het eerste getal op de lijst. We kiezen op dezelfde manier een tweede decimaal: als de tweede decimaal van het tweede getal op de lijst geen 2 is, kiezen we een 2, anders een 1. Enzovoorts.

Een voorbeeld van een hypothetische lijst met de constructie van een stukje van het nieuwe getal.

Dit nieuwe getal staat nergens op de lijst. Ga maar na: het is niet gelijk aan het eerste getal op de lijst, want de eerste decimaal verschilt. Het is ook niet gelijk aan het 37e getal, want de 37e decimaal verschilt. Kortom: het nieuwe getal ontbreekt op de lijst, wat de lijst ook was! Maar het zou er wel op moeten staan, want het is een getal tussen 0 en 1. Dat betekent dat de getallen tussen 0 en 1 niet op een lijst te zetten zijn, en er dus geen koppeling bestaat met de aftelbare verzameling 1, 2, 3, … . Echt een ander soort oneindig, dus!

Deze column verscheen gisteren in de Volkskrant.

Genieën spreken tot de verbeelding. En als gewone mensen opeens een onontdekt genie blijken te zijn, spreekt dat nog veel sterker tot de verbeelding. Want wie weet! Misschien hebben wij zelf ook wel een onontdekt groot talent dat ons eeuwige roem en geluk zal brengen! Er is dan ook een niet aflatende stroom aan tv-programma’s te zien die ons, de gewone mensen, uitdagen om onze talenten aan de rest van de wereld te laten zien.

En al is wiskunde misschien niet zo geschikt voor een talentenjacht op televisie, er zijn wel degelijk anekdotes in omloop over onontdekte wiskundegenieën. Een van de bekende urban legends over zo’n wiskundegenie gaat ongeveer als volgt: een gewone student komt een wiskundeprobleem tegen, gaat eraan werken, en lost het op. Zonder te weten dat het betreffende probleem een open, onopgelost wiskundeprobleem was waar de grote geesten hun tanden al op stukgebeten hadden.

Deze verhaallijn zie je terug in de film Good Will Hunting. Een jonge schoonmaker (gespeeld door Matt Damon) maakt de gangen van het MIT schoon en leest zodoende een wiskundevraagstuk op een schoolbord. Hij gaat aan de slag, en jawel: lost het op. Het zogenaamd onopgeloste probleem op het schoolbord in deze film is trouwens in werkelijkheid een standaardopgave die een gemiddelde wiskundestudent makkelijk moet kunnen maken, maar dat is een ander verhaal.

Hoe onwaarschijnlijk de situatie in Good Will Hunting ook is (zonder opleiding is het feitelijk onmogelijk om wiskundenotatie te lezen, hoe slim je ook bent, want dat is gewoon een hele rits afspraken waarvan je weet moet hebben), er zit wel een kern van waarheid in.

In 1939 ging George Dantzig, student in Berkeley, naar een college van professor Jerzy Neyman. Hij was te laat. Toen hij binnenkwam, stonden er twee statistiekproblemen op het bord. Hij nam aan dat het de huiswerkopgaven waren voor deze week, schreef ze over en ging er aan werken. Ze leken wat moeilijker dan anders. Meestal kreeg hij zijn huiswerk wel in een paar uur af, maar nu had hij een paar dagen nodig. Met excuses bracht bij ze naar Neyman, die hem sommeerde het huiswerk maar op zijn bureau te leggen. Een week of zes later bonkte Neyman op zondagochtend opgewonden bij Dantzig op de deur: “Ik heb een inleiding geschreven bij je artikel! Lees het snel even door, dan kan ik het direct opsturen voor publicatie!” Dat was het moment waarop Dantzig merkte dat hij iets bijzonders gedaan had: de problemen die hij opgelost had, bleken open problemen te zijn.

Dantzigs oplossingen werden de basis voor zijn dissertatie. En ook later deed hij belangrijke dingen: hij bedacht de zogenaamde simplexmethode, een methode die veel gebruikt wordt bij optimaliseringsproblemen (denk aan maximaliseren van productie, of het minimaliseren van kosten).

Ik zie deze anekdote persoonlijk liever als een stimulans tot een open blik dan als een verhaal over een onvermoed genie. Dantzig was onbevooroordeeld. Hij wist niet dat het vraagstuk een bekend open probleem was, dus hij benaderde het als ieder ander huiswerkprobleem. Moeilijk, maar ja, het was een huiswerkopgave, dus uiteindelijk zou het moeten lukken. En zo was het.

Deze column verschijnt vandaag in de Volkskrant.

Een van de grootste misverstanden omtrent wiskunde is dat mensen die wiskunde leuk vinden het ook altijd makkelijk vinden. Dat is niet zo: iedereen komt vanzelf op een punt dat hij het niet meer snapt. Een belangrijk verschil tussen mensen die zichzelf goed of juist slecht in wiskunde vinden, is hoe ze daar vervolgens mee omgaan.

Voor wiskundigen begint de uitdaging dan pas! Ze gaan met frisse moed het probleem te lijf, bereiden zich mentaal voor op een serie frustraties en vertrouwen erop dat doorzetten uiteindelijk zal leiden tot, in het ideale geval, een euforisch gevoel van begrip: “ja natuurlijk zit het zo!” En soms duurt dat heel lang. Of komt het niet. Kan gebeuren.

Mensen met wiskundeangst (math anxiety) gaan daar heel anders mee om. Meestal hebben ze in hun schooltijd op een bepaald moment een gevoel van “sudden death” ervaren, schrijft Sheila Tobias in haar boek “Overcoming math anxiety”. Bij haarzelf kwam dat toen ze leerde dat hetzelfde betekent als . Ze snapte dat het consistent was met de regels voor machten, maar dat voelde niet als een echte uitleg. En toen kreeg ze het gevoel dat het niet alleen moeilijk was om het te begrijpen, maar zelfs fundamenteel onmogelijk. Een irrationele reactie, maar eentje die veel vaker voorkomt. Meestal gepaard aan het gevoel dat eerdere wiskundesuccessen dus blijkbaar “gefaket” waren. Mensen met wiskundeangst gaan fouten vermijden in plaats van onderzoeken, en geloven vaker dat wiskunde iets is dat je kunt of niet kunt, een aangeboren eigenschap waar je niets aan kunt veranderen.

Waarom is juist wiskunde eng? Wiskunde bouwt sterk voort op eerder opgedane vaardigheden, als je ergens een steek hebt laten vallen is het moeilijk die weer op te halen. Er is druk om “het goede antwoord” te geven, met de onterechte implicatie dat er altijd maar één goed antwoord is. En wiskunde, hoe exact ook, is soms onverwacht dubbelzinnig zonder dat dat expliciet gemaakt wordt. In en betekenen de =-tekens iets heel verschillends: het eerste geeft aan dat de vergelijking opgelost moet worden, het tweede dat de bewering waar is, welk getal ook is. Dat blijkt echter niet uit de vorm van de uitdrukking. Dat soort dubbelzinnigheden kunnen verwarring opleveren, en een gevoel van onmacht.

Om wiskundeangst te voorkomen is het belangrijk om als docent of ouder te benadrukken dat het denkproces belangrijker is dan het eindantwoord. Dat wiskunde niet iets is wat je kan of niet kan, maar dat je kan (moet) oefenen. Dat al die wiskunde ergens vandaan komt, door mensen bedacht is om echte vragen op te lossen, en dat je ook in wiskundesommen creatief kunt zijn. Dat samenwerken productief is. En vooral: niet opgeven.

In 2010 werd in een Amerikaans onderzoek aangetoond dat wiskundeangst bij leraressen op de vroege basisschool (en negentig procent van die docenten is vrouw) meisjes in hun klas (maar niet de jongens!) negatief beïnvloedt: zij geloven vaker dat meisjes niet goed zijn in wiskunde, en hun wiskundeprestaties blijven achter. Genoeg reden om wiskundeangst als een probleem te zien, zeker bij leraren (in opleiding).

Deze column verscheen afgelopen zaterdag in de Volkskrant.

Wiskunde tegenkomen in oude, verdwenen culturen is fascinerend. De wiskunde van de Babyloniërs in het oude Mesopotamië, bijvoorbeeld, is heel interessant. Mesopotamië lag ongeveer in het huidige Irak, en onder “Babyloniërs” verstaan we een hele serie volkeren in dat gebied, zo tussen 3000 en 500 voor Christus.

Het fijne aan de Babyloniërs is dat ze schreven op duurzaam materiaal: kleitabletten. Die kunnen we lezen, als we de taal en het spijkerschrift snappen, tenminste. Maar Babylonische getallen zijn zelfs voor een leek makkelijk te ontcijferen.

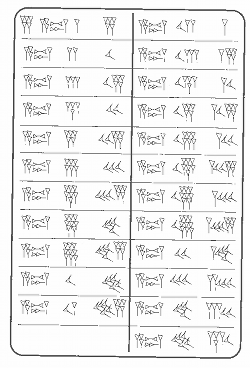
Op het plaatje staat een transcriptie van een kleitablet. In de middelste kolom staat een rij symbolen: één spijkertje op de eerste regel, twee spijkertjes op de tweede, enzovoorts. In die kolom staan inderdaad de getallen 1, 2, 3, 4, 5, …. Na de negen verschijnt een nieuw symbool, een soort winkelhaakje, dat blijkbaar voor de tien staat.

Wat staat er in de derde kolom? Naast de 1 staat 5, en naast de 2 staat 10. Naast de 3 staan een 10 en een 5, dat zal dan wel 15 betekenen. Deze regelmaat vervolgt zich, en het is duidelijk wat hier staat: de tafel van vijf. Dat clustertje tekens vooraan elke regel betekent “keer”.

Bij vijf keer twaalf gebeurt er iets geks: de uitkomst is 1 spijker, wat, zagen we al, één betekent. Maar vijf keer twaalf is zestig! Blijkbaar betekent een spijker behalve één ook zestig. Wat onhandig, denk u misschien. Aan de andere kant: wij gebruiken een 1 ook op verschillende manieren, in het getal 123 betekent de 1 dat er één honderdtal is.

Net als wij kenden de Babyloniërs een zogenaamd positiestelsel. De plaats van een cijfer in een getal bepaalt hoeveel het cijfer waard is. De Babyloniërs gebruikten als grondtal zestig, waar wij tien gebruiken. Als zij met hun spijkerschrift 2; 15; 51 opschreven, bedoelden ze 2 keer 3600 (want 60 × 60 = 3600), 15 keer zestig en 51 keer één.

Of misschien wel 2 zestigen, 15 enen en 51 zestigsten! Want er is een belangrijk verschil: ze hadden geen komma en heel lang ook geen symbool voor een lege plaats. Wij zien door nullen, die eigenlijk lege plekken aangeven, makkelijk het verschil tussen 100 en 1. En dat we met 0,1 een tiende bedoelen, zien we aan de komma. De Babyloniërs niet. Meestal was dat niet zo’n probleem, want uit de context bleek vaak wel wat er bedoeld werd.

Een voordeel van een positiestelsel is dat je er makkelijk in kan rekenen door getallen onder elkaar te zetten. De Babyloniërs konden overigens veel meer dan rekenen alleen, zo kenden ze de stelling van Pythagoras en losten ze bepaalde kwadratische vergelijkingen op.

Een Babylonisch kleitablet met een goede benadering van erop.

Het getalstelsel van de Babyloniërs is helaas in onbruik geraakt en er doken veel onhandigere getalstelsels op, zoals de Romeinse cijfers. Probeer die maar eens onder elkaar te vermenigvuldigen… Pas in de dertiende eeuw kwam een Indiaas positiestelsel via de Arabische wereld onze kant op, en werd het rekenen hier makkelijk. Wat we wèl overgehouden hebben aan de Babyloniërs, is onze zestigtallige tijdrekening.

Deze column verschijnt vandaag in de Volkskrant.

Op de lerarenopleiding moest ik een puzzel uit de experimentele psychologie oplossen. Stel, er liggen vier kaartjes op tafel. Elk kaartje heeft aan de ene kant een letter en aan de andere kant een cijfer. Op de kanten die je kunt zien, staan een A, een B, een 4 en een 7. Vervolgens beweert iemand: “Voor deze vier kaartjes geldt: als er aan de ene kant een klinker staat, staat aan de andere kant een even getal”. Welke kaartjes moet je minstens omdraaien om zeker te weten of de bewering klopt?

Denk eerst even goed na voor u verder leest!

Deze vraag werd in 1966 bedacht door cognitief psycholoog Peter Wason en hij ontdekte dat nog geen tien procent van de mensen het antwoord goed had. In mijn groep docenten in opleiding hadden gelukkig wel wat meer mensen het goed, en de wiskundigen wisten het allemaal meteen. Niet zo gek ook, want die zijn gewend aan ingewikkelde als-dan-redeneringen.

En wat is het goede antwoord? Je moet natuurlijk het kaartje met de A omdraaien (want je moet controleren of aan de andere kant inderdaad een even getal staat). Dat doet iedereen wel goed. Er is nog een kaartje dat je moet omdraaien: de 7. De enige manier waarop de bewering ontkracht kan worden, is namelijk een kaartje vinden met een klinker en een oneven getal. Je moet de 7 dus omdraaien om te zien of er niet per ongeluk een klinker aan de andere kant staat. De 4 en de B kun je rustig laten liggen, want er is niet gezegd dat een even getal altijd een klinker op de andere kant moet hebben, en voor medeklinkers is überhaupt geen eis gesteld.

Later ontdekte men dat veel meer mensen het antwoord goed hebben wanneer de vraag in een sociale context gepresenteerd wordt. Als aan de ene kant leeftijden en aan de andere kant dranken staan, en de bewering is “als iemand jonger dan 16 is, drinkt hij/zij geen alcohol”, en je vervolgens de kaartjes cola, bier, 12 en 19 laat zien, schijnt het veel makkelijker te zien te zijn welke kaartjes je moet omdraaien. Het kaartje met bier (je moet controleren of daar geen leeftijd jonger dan 16 bij hoort) en het kaartje met 12 (drinkt die persoon van 12 niet stiekem een breezer?). Wat de leeftijd is van de persoon die cola drinkt en of de persoon van 19 alcohol nuttigt, zijn totaal niet relevant, vergelijkbaar met de 4 en de B in het oorspronkelijke probleem.

Deze situaties zijn natuurlijk niet helemaal hetzelfde: de eerste regel is willekeurig, opgesteld door de onderzoekers, terwijl de tweede regel een wet is die we allemaal kennen, waar al een sterke normatieve associatie bijhoort. Maar wat betreft de logica komt de situatie overeen.

Veel mensen hebben in de eerste puzzel de neiging om het kaartje met de 4 ook om te draaien. Maar je controleert dan in feite of de wet wordt nageleefd door te kijken wat de leeftijd is van iemand die cola drinkt.

Deze column verscheen zaterdag in de Volkskrant.

“Een ruzie met familie of je partner zit je nogal dwars.” Aldus mijn horoscoop uit een damesblad van vorige week. Ik lees hem pas nu en heb de hele week geen ruzie gehad, noch zat me anderszins iets dwars in mijn relatie met familie dan wel vriend.

Tijdschrifthoroscopen sla ik altijd over. Waarom zou iedereen die toevallig ook tussen 21 april en 20 mei geboren is de komende week hetzelfde gaan meemaken als ik?

Toch bestaat er een belangrijk, wellicht verrassend, historisch verband tussen wiskunde en astrologie. Astrologie was namelijk lange tijd een serieuze, dankbare toepassing van de wiskunde, in een tijd dat toepassingen waarvan iedereen het nut nu inziet (GPS, beveiligd internetbankieren, computers, modellen om het weer te voorspellen enzovoort enzovoort) nog verre toekomstmuziek waren.

Ontkennen dat hemellichamen invloed hebben op het leven hier op aarde kan natuurlijk niet: al het leven bestaat dankzij de energie van de zon, wanneer de zon aan de hemel staat gaan we aan het werk en als de zon onder is slapen we, en de positie van de maan beïnvloedt duidelijk hoe hoog het water staat. Maar dat de relatieve positie van planeten, zoals we die vanaf de aarde zien, kan beïnvloeden hoe ons leven verloopt, hoe ons karakter is of bepaalt welke beslissing je het beste kan nemen… Nee, daar laten de meeste mensen zich tegenwoordig niet door leiden.

Maar dat is dus niet altijd zo geweest: in de middeleeuwse islamitische wiskunde (die zeer hoog ontwikkeld was, terwijl West-Europa zich in de donkere middeleeuwen bevond) waren horoscopen een belangrijke aanleiding voor onderzoek. Islamitische theologen hadden wel bezwaar tegen astrologie, maar omdat het ook nuttig was de richting van Mekka of precieze gebedstijden te kunnen berekenen, kwamen de wetenschappers daar vaak wel mee weg.

Een astroloog moest in staat zijn de precieze stand van de hemellichamen op elk gegeven moment te kunnen uitrekenen, want hoe beter hij dat kon, hoe beter de voorspelling en hoe hoger zijn status. Zo’n horoscoop werd trouwens meestal berekend voor het precieze geboortemoment van één persoon, dit in tegenstelling tot de damesbladhoroscoop van hierboven.

Voor die berekeningen waren astronomische tabellen nodig met een heleboel gegevens. Als die tabellen na verloop van tijd niet meer helemaal klopten met de waarnemingen, moesten ze worden aangepast, waar ingewikkelde meetkunde bij nodig was. Een goede astroloog was dan ook geschoold in geavanceerde wiskunde, bijvoorbeeld die uit de Griekse oudheid. Veel wiskunde uit de Griekse oudheid is dankzij de islamitische wereld bewaard gebleven.

De astrologie gaf wiskunde en astronomie dus maatschappelijke relevantie, zorgde voor behoefte aan wiskundeonderwijs, en bovendien was deze toepasbaarheid goed voor het imago van de wiskunde (net als nu eigenlijk, al zijn de toepassingen heel anders).

Ook beroemde Europese wetenschappers als Tycho Brahe en Galileo Galilei werkten aan astrologie. Omdat dat zó niet past bij ons ideaalbeeld van de rationele wetenschap, vergeten we dit soort historische feiten misschien liever. Maar het is interessant om te zien hoe anders mensen, en dus ook wetenschappers, vroeger naar het universum keken.