Wiskundemeisjes

Laat ik dit even vooropstellen: ik houd niet zo van Facebookquizzen. En ik hoef ook niet per se te zien op wat voor wortel of stripfiguur of Friends-personage mijn vrienden het meest lijken, al is het maar omdat ik me dan onwillekeurig ga afvragen welke onverwachte kanten van mijn vrienden ik nog nooit gezien heb. Maar ik zat thuis een beetje ziek te zijn, en ik zag opeens allerlei wiskundige Facebookquizzen langskomen (want ik ken natuurlijk een boel wiskundigen op Facebook), en dat is uiteraard een heel ander verhaal! Dus voor de mensen die wel van Facebookquizzen houden bij wijze van studie- of werkontwijkend gedrag: hier zijn er een paar die met wiskunde te maken hebben, inclusief mijn resultaten.
De eerste die ik deed:
Jeanine completed the quiz "What Kind of Mathematician Are You?" with the result Logician.

You are a logician. Although you will probably disagree with me on that to say you have a more specific discipline. You tend to be very pedantic and serious. You are probably overly concerned with your grammar and spelling - not to mention that of others. This is not a bad character trait! You are the ones your friends go to when they need help finding the flaw in their proof. In fact... Does my quiz rely on the Axiom of Choice?
En de tweede:
Jeanine took the Which mathematical function are you? quiz and the result is Gaussian: e^(-x^2)
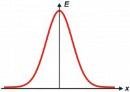
You are centered. You are just where you want to be. Some mistake your quiet nature for mediocrity, but you are anything but ordinary. You don't show of, you don't brag, but you have a rich inner life. Few realize how important you are. But that does not bother you. Life is good.
En de derde:
Jeanine took the What branch of mathematics are you? quiz and the result is Number Theory

Most people will never meet you until they get to college. When they first get to know you, you seem pretty simple-minded. "An even number plus and odd number is an odd number," you tell them, and all they say is, "So?" But then you ask them something hard, like, "Are there any integers a, b, and c that satisfy the equation x to the n plus y to the n equals z to the n when n is greater than 2?" And it takes them well over 300 years to figure out the answer. Who's laughing now, idiots?!
En het houdt niet op:
Jeanine took the Which Mathematical Symbol Are You? quiz and the result is Absolute Value
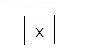
An absolute value sign! You are care free and imaginative. Everything complex can be simplified to you, and nothing matters a whole lot. You take life in stride and never worry too much.
En jawel:
Jeanine took the Which mathematician are you? quiz and the result is Carl Friedrich Gauss

Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, electrostatics, astronomy and optics. Sometimes known as the Princeps mathematicorum and "greatest mathematician since antiquity", Gauss had a remarkable influence in many fields of mathematics and science and is ranked as one of history's most influential mathematicians. He referred to mathematics as "the queen of sciences."
En er zijn er nog veel meer (er zijn natuurlijk ook quizzen om de testen of je goed bent in wiskunde, bijvoorbeeld), maar toen vond ik het wel weer mooi geweest: zelfs op Facebook gingen mensen vragen of ik niet aan mijn proefschrift hoorde te werken.
Wiskundige lijkt een veilig beroep. Wat kan je nu gebeuren achter je bureau tussen je stapels papieren en je computer?
Jullie konden het al lezen in de Spits van vandaag: de wiskundemeisjes gaan van start met een nieuwe serie. Hendrik Lenstra kwam op het idee om eens te kijken hoe wiskundigen om het leven zijn gekomen. Er kwamen verbijsterende verhalen naar boven. Elke maand bespreken we voortaan een wiskundige die op een bijzondere wijze aan zijn eind gekomen is.

Zo'n wiskundige is de beroemde Kurt Gödel. We schreven al eerder over Gödel en zijn onvolledigheidsstelling en over de film die onlangs over zijn leven gemaakt werd.
Maar hoe kwam Gödel aan zijn eind? Toen hij ouder werd, raakte hij paranoïde. Hij was ervan overtuigd dat iemand hem wilde vergiftigen en daarom wilde hij alleen dingen eten die door zijn vrouw Adele bereid waren. Toen zij ziek werd en niet meer voor hem kon koken, weigerde hij te eten. Uiteindelijk stierf hij in Princeton op 14 januari 1978. Hij is 71 jaar oud geworden. In zijn overlijdensrapport staat dat hij stierf aan "starvation and inanition, due to personality disorder".
Mooie foto's uit Gödels leven zijn te vinden op deze site, naar aanleiding van een tentoonstelling over hem in Wenen.

Verschillende mensen mailden ons, maar de wiskundemeisjes hadden het ook al in hun agenda's staan: Donderdag 6 september om 00.15 uur* is op Nederland 2 de film Gödel te zien. We schreven hier al over deze film die gemaakt is door eindexamenkandidaten van de Nederlandse Film en Televisie Academie. HJ merkte toen in de reacties op dat de biografie van Gödel op de site van de film niet helemaal klopt:
“In 1928 hield de Duitse wiskundige David Hilbert een voordracht op het wiskunde congres congres [sic] in Bologna, waarin hij een aantal grote onopgeloste problemen van het wiskundige wiskundige [sic] grondslagen-onderzoek van zijn tijd uiteenzette.” [..] “Nog geen twee jaar later had de 24-jarige Kurt Gödel alle stellingen van Hilbert definitief opgelost.” Bijna goed.
De producent Jeroen J. Meijer verklaarde dat de tekst op site inderdaad wat onjuistheden bevat. We hopen maar dat de film dichter bij de waarheid ligt. Logicus Henk Barendregt werkte eraan mee, dus dat schept goede hoop! De wiskundemeisjes gaan in elk geval kijken...
(Ionica)
* Voor de muggenzifters: eigenlijk is de film dus op vrijdag te zien...
In de categorie wiskunde en kunst zijn er volgende week maar liefst twee leuke uitjes die je kunt maken!

Afstudeerders van de Nederlandse Film- en Televisie Academie maakten een film over Kurt Gödel. Dit is de omschrijving:
De logicus Kurt Gödel wordt aan het eind van zijn leven geconfronteerd met een werkelijkheid, die hem voor nieuwe filosofische problemen stelt en de aard van zijn bestaan in twijfel trekt.
Wij zijn benieuwd! De film is van 26 tot en met 30 juni te zien in Amsterdam. Kijk hier voor de precieze tijden. Bij de film hoort ook een mooie website. Kijk ook even naar de lange lijst met wiskundige sponsors.
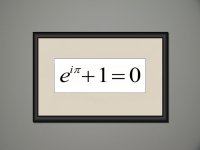
Op donderdag 28 juni zingt het Groot Omroepkoor eιπ + 1 = 0 or, the most remarkable formula in the world, geschreven door MaNOj Kamps. Dit a capella stuk gaat samen met vier andere composities in première in Haarlem. Deze werken zijn gekozen uit 135 inzendingen voor een compositiewedstrijd. Kijk hier voor meer informatie en kaarten. We weten dat MaNoJ wel eens op de wiskundemeisjes komt, dus misschien wil hij in de reacties iets meer vertellen over zijn compositie...
(Ionica)
ps Inmiddels heeft MaNoJ inderdaad gereageerd en kun je in zijn reactie veel meer lezen over de compositie.

Vandaag is de honderdste geboortedag van Kurt Gödel (1906 - 1978). Ik ga vandaag niets over zijn leven schrijven, want informatie daarover kun je bijvoorbeeld lezen in zijn In Memoriam uit The Times of een moderner artikel van Christian Jongeneel.
Gödel is vooral bekend om zijn onvolledigheidsstelling. Die stelling heeft betrekking op het logische bouwsel van axioma's en stellingen dat de wiskunde is. De wiskunde is gebaseerd op axioma's, de fundamenten van de wiskunde. De axioma's zijn beweringen die je aanneemt. Door middel van de regels van de logica kun je uit die axioma's stellingen afleiden. Een stelling is dus een bewering waarvoor een bewijs, zo'n logische afleiding, is gevonden. De onvolledigheidsstelling is dus eigenlijk een meta-stelling: het is een wiskundige stelling die tegelijk iets zegt over de wiskunde zelf als formele taal.
De belangrijkste eis die wiskundigen stellen aan dit formele systeem is dat het consistent moet zijn. Dat houdt in dat in zo'n systeem alleen ware beweringen bewezen mogen kunnen worden, oftewel: als een bewering niet waar is, mag hij niet bewijsbaar zijn.
De wiskundigen uit het begin van de twintigste eeuw, bijvoorbeeld Russell en Hilbert, probeerden de hele wiskunde op die manier om te toveren tot een formele taal. Hun ultieme hoop was dat het mogelijk zou zijn om in zo'n consistent systeem alle ware beweringen ook daadwerkelijk te bewijzen.
Deze hoop werd door Gödel in 1931 de grond in geboord. Hij bewees toen namelijk zijn onvolledigheidsstelling: als je een voldoende sterk, consistent formeel systeem hebt, met de regels van de logica, dan bestaan er altijd beweringen die wel waar zijn, maar niet binnen dit systeem te bewijzen zijn! ("Voldoende sterk" betekent hier dat het systeem minstens de rekenkunde moet omvatten, wat voor een wiskundig systeem natuurlijk niet teveel gevraagd is.)
Het idee van het bewijs is gebaseerd op zelfverwijzing. Gödel is er op een slimme manier in geslaagd om binnen het systeem de volgende bewering te formuleren: "Deze bewering is onbewijsbaar". Nu zijn er natuurlijk twee mogelijkheden. De eerste mogelijkheid is dat de bewering onwaar is. Maar dan is de bewering niet onbewijsbaar, dus bewijsbaar. Dan hebben we een bewering gevonden die onwaar is en toch bewijsbaar! Maar dat is in tegenspraak met de consistentie van ons formele systeem. Deze mogelijkheid valt dus af.
De enige andere mogelijkheid is dat de bewering waar is. Maar nu volgt natuurlijk dat de bewering onbewijsbaar is. Het systeem bevat dus minstens één bewering die waar is, maar niet bewijsbaar. Omdat je dit in elk dergelijk formeel systeem kunt doen, is bewezen dat al die systemen onvolledig zijn.
Voor de wiskundige praktijk heeft de onvolledigheidsstelling veel minder gevolgen dan je misschien zou verwachten. Er is nog nooit een dergelijke zin gevonden die niet speciaal als voorbeeld geconstrueerd is met behulp van die zelfverwijzing. Dat komt natuurlijk ook omdat het in principe niet zo makkelijk is om van een bewering wel te weten dat ze waar is, terwijl er geen bewijs bestaat...
(Jeanine)
 Internetbureau Rotterdam
Internetbureau Rotterdam 
