Wiskundemeisjes

Op het onvolprezen weblog n-Category café stelde John Baez deze week een interessante vraag: hoe groot schat je de kans dat bepaalde beroemdheden echt hebben bestaan? Baez geeft een lijst namen met daarbij zijn eigen schattingen. Bijvoorbeeld

• Adam - 5%
• Homerus - 30%
• Pythagoras - 60%
• Robin Hood - 60%
• Nicolas Bourbaki - 0%

Kijk hier voor de complete lijst van Baez en probeer vooral om zelf de kansen te schatten. De reacties zijn geweldig en lopen een beetje uit de hand als de lezers moppen gaan verzinnen met personages uit de lijst - met beginzinnen als: Osama bin Laden, Santa Claus and Pythagoras walk into a bar...

Voor het geval jullie -geheel onterecht- nog niet naar de originele pagina zijn gegaan, deze anekdote over Littlewood wil ik jullie niet onthouden: Littlewood has a story in his Miscellany, of meeting someone who said “Oh, you really exist! I thought you were just a pseudonym that Hardy put on his weaker papers.”

(Ionica - 100%)

Vorige week schreef Martijn van ThinkSmall een heel grappig stukje over wiskunde. Wij hadden het in de tussentijd zo druk met hartjes maken voor Valentijnsdag dat we er nog niet eerder aan toe kwamen om het te linken.

Martijn interviewde in 2002 Robert Schneider van de band Apples in Stereo. De zanger werd laaiend enthousiast toen hij hoorde dat Martijn promoveerde in de wiskunde. Martijn en hij wisselden daarna nog een paar emails uit over wiskunde. Lees vooral zelf wat Martijn daar over schrijft, het is een erg grappig verhaal.

En wat schrijft Stylus over het nieuwe album van Apples in Stereo?

… Schneider went so far as to create a new musical language, the Non-Pythagorean Music Scale, for the album. A novel if not exactly new concept, he used equations based on the properties of natural logarithms to replace the standard 12 tones in a musical octave with a different set of frequencies. Several of these new frequencies show up in the 12 instrumental link tracks that segue between the 14 “eal” songs, à la Her Wallpaper Reverie, making New Magnetic Wonder a sprawling mass of tunes and teasers. For the most part, the link tracks work as palette cleansers; teeth brushing for Schneider’s saccharine tunes.

Maar verder klinkt het nog steeds heel leuk...

(Ionica)

Ongelooflijk, komt er een leuke wiskundeleraar op bezoek bij Paul de Leeuw, krijgt hij tien minuten de tijd om les te geven aan een groot publiek, mis ik dat! Gelukkig staat de hele uitzending nog op internet...

Swier Garst is de leuke wiskundeleraar in kwestie en hij was 6 mei te gast bij Mooi Weer de Leeuw. Hieronder zien we hem met Arjo, een van zijn leerlingen, en Paul de Leeuw.

Swier verzuchtte soms als hij voor het bord stond, dat hij zo graag eens voor meer dan twintig mensen les zou geven. Arjo aarzelde niet en stuurde Paul de Leeuw een email met dit verzoek en zo mocht Swier aan Paul de Leeuw en zo'n 800.000 kijkers de Stelling van Pythagoras uitleggen.

Paul de Leeuw snapte er al snel geen iota meer van, hoewel Swier nog van die aansprekende voorbeelden met chocolade gebruikte. Swier maakte ook erg veel grappen, over de rechte lijn van Verdonk bijvoorbeeld. Zou hij dat op school ook zo doen?

Als je Swier ook wil zien: ga op de site van Mooi Weer de Leeuw naar de Afterparty van 6 mei. Skip naar 36 minuten vanaf het begin, lach even om de afgrijselijke jongensband die je ziet en wacht tot Swier van de tribune wordt gehaald. En als er nog eens zoiets leuks op televisie komt, kan iemand mij dan even emailen?

(Ionica)

Deze column verscheen afgelopen zaterdag in de Volkskrant.

Wiskunde tegenkomen in oude, verdwenen culturen is fascinerend. De wiskunde van de Babyloniërs in het oude Mesopotamië, bijvoorbeeld, is heel interessant. Mesopotamië lag ongeveer in het huidige Irak, en onder “Babyloniërs” verstaan we een hele serie volkeren in dat gebied, zo tussen 3000 en 500 voor Christus.

Het fijne aan de Babyloniërs is dat ze schreven op duurzaam materiaal: kleitabletten. Die kunnen we lezen, als we de taal en het spijkerschrift snappen, tenminste. Maar Babylonische getallen zijn zelfs voor een leek makkelijk te ontcijferen.

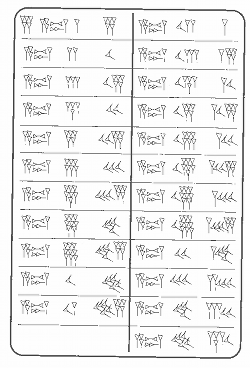
Op het plaatje staat een transcriptie van een kleitablet. In de middelste kolom staat een rij symbolen: één spijkertje op de eerste regel, twee spijkertjes op de tweede, enzovoorts. In die kolom staan inderdaad de getallen 1, 2, 3, 4, 5, …. Na de negen verschijnt een nieuw symbool, een soort winkelhaakje, dat blijkbaar voor de tien staat.

Wat staat er in de derde kolom? Naast de 1 staat 5, en naast de 2 staat 10. Naast de 3 staan een 10 en een 5, dat zal dan wel 15 betekenen. Deze regelmaat vervolgt zich, en het is duidelijk wat hier staat: de tafel van vijf. Dat clustertje tekens vooraan elke regel betekent “keer”.

Bij vijf keer twaalf gebeurt er iets geks: de uitkomst is 1 spijker, wat, zagen we al, één betekent. Maar vijf keer twaalf is zestig! Blijkbaar betekent een spijker behalve één ook zestig. Wat onhandig, denk u misschien. Aan de andere kant: wij gebruiken een 1 ook op verschillende manieren, in het getal 123 betekent de 1 dat er één honderdtal is.

Net als wij kenden de Babyloniërs een zogenaamd positiestelsel. De plaats van een cijfer in een getal bepaalt hoeveel het cijfer waard is. De Babyloniërs gebruikten als grondtal zestig, waar wij tien gebruiken. Als zij met hun spijkerschrift 2; 15; 51 opschreven, bedoelden ze 2 keer 3600 (want 60 × 60 = 3600), 15 keer zestig en 51 keer één.

Of misschien wel 2 zestigen, 15 enen en 51 zestigsten! Want er is een belangrijk verschil: ze hadden geen komma en heel lang ook geen symbool voor een lege plaats. Wij zien door nullen, die eigenlijk lege plekken aangeven, makkelijk het verschil tussen 100 en 1. En dat we met 0,1 een tiende bedoelen, zien we aan de komma. De Babyloniërs niet. Meestal was dat niet zo’n probleem, want uit de context bleek vaak wel wat er bedoeld werd.

Een voordeel van een positiestelsel is dat je er makkelijk in kan rekenen door getallen onder elkaar te zetten. De Babyloniërs konden overigens veel meer dan rekenen alleen, zo kenden ze de stelling van Pythagoras en losten ze bepaalde kwadratische vergelijkingen op.

Een Babylonisch kleitablet met een goede benadering van erop.

Het getalstelsel van de Babyloniërs is helaas in onbruik geraakt en er doken veel onhandigere getalstelsels op, zoals de Romeinse cijfers. Probeer die maar eens onder elkaar te vermenigvuldigen… Pas in de dertiende eeuw kwam een Indiaas positiestelsel via de Arabische wereld onze kant op, en werd het rekenen hier makkelijk. Wat we wèl overgehouden hebben aan de Babyloniërs, is onze zestigtallige tijdrekening.

Deze column verschijnt vandaag in De Volkskrant.

Van wiskunde op de middelbare school herinneren veel mensen zich maar twee dingen: de stelling van Pythagoras en de wanhopige vraag waar al die sommen goed voor zijn. Mijn eigen wiskundedocent had helaas nooit een erg bevredigend antwoord op die vraag. En dat terwijl je alleen de stelling van Pythagoras al kunt gebruiken bij het maken van een boomhut of het bestellen van pizza’s.

De eeuwenoude stelling gaat over een rechthoekige driehoek. In zo’n driehoek is het kwadraat van de lengte van de schuine zijde gelijk aan de kwadraten van de lengtes van de twee rechthoekszijden bij elkaar opgeteld. Oftewel: (waarbij en de lengtes van de rechtshoekzijden zijn en de lengte van de schuine zijde).

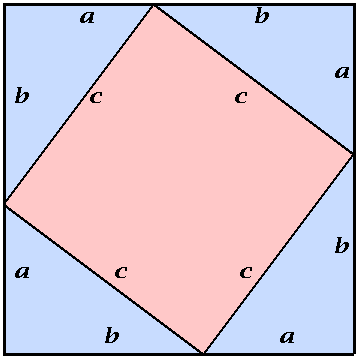
Een plaatjesbewijs voor de stelling van Pythagoras

Op school wordt de stelling vooral gebruikt om de lengte van zijden te bepalen in allerlei driehoeken, parallellogrammen en andere figuren. Maar de stelling van Pythagoras kan ook nuttig zijn bij meer alledaagse problemen, bijvoorbeeld bij het maken van een boomhut (of een hekje, of een schuurtje). Ze helpt je namelijk om zonder geodriehoek of winkelhaak een perfecte rechte hoek te construeren. Je hebt alleen een stukje touw nodig, een mes en iets om mee te meten. Snijd drie stukken touw af van 30, 40 en 50 centimeter en leg deze stukken in een driehoek. De hoek tussen de stukken van 30 en 40 centimeter is nu een rechte hoek, dus daarmee kun je je de wanden van je boomhut keurig haaks op elkaar spijkeren. De driehoek van touw heeft zijden van 30, 40 en 50 centimeter en (dus ).

Scherpe lezers zullen opmerken dat je eigenlijk niet eens touw nodig hebt voor deze truc. Alleen iets om te te meten is ook al genoeg. Nog scherpere lezers zullen opmerken dat hierbij niet de stelling van Pythagoras wordt gebruikt, maar haar omkering. Als namelijk in een driehoek met zijden en geldt dat , dan is het een rechthoekige driehoek. Dat vertellen ze helaas bijna nooit op de middelbare school.

En wat ze al helemaal niet vertellen is dat je de formule ook kunt gebruiken voor andere vormen dan driehoeken, bijvoorbeeld voor cirkels. Stel dat je in een pizzeria twijfelt: op de kaart staan pizza’s met een diameters van 18, 24 en 30 centimeter. Je bent met een groep en vraagt je af of je beter twee kleine pizza’s kunt nemen of één grootte. Maar dan bedenk je dat . En dat betekent dat de twee pizza’s van 18 en 24 centimeter samen precies even groot zijn als één pizza van 30 centimeter (reken het maar na). Waarschijnlijk ben je een stuk goedkoper uit met één grote pizza. Daar is wiskunde dus goed voor.

Deze column verschijnt vandaag in de Volkskrant.

Wiskunde is toepasbaar op vele gebieden van het leven, ook waar je het misschien niet direct verwacht. De liefde, bijvoorbeeld. Er zitten wiskundige ideeën achter de koppelalgoritmes van datingsites, en je kunt wiskundig modelleren wat voor cadeau je iemand moet geven die je zou willen versieren: iets dat jou veel moeite kost, maar waardeloos is voor de ander als hij of zij niet in jou, maar wel in materiële zaken geïnteresseerd is. Zoals een ingewikkeld, zelfgekookt diner voor twee.

Maar als je de liefde van je leven eenmaal gevonden hebt, kan de wiskunde dan nog wat toevoegen aan dit geluk?

Ik was vorige week op een feestje van een vriend en zijn vriendin, die tijdens het feest stralend vertelden dat ze stiekem getrouwd waren. Deze vriend is een wiskundige, en hij liet me zien dat het getal 220 in zijn trouwring stond. In de ring van zijn kersverse echtgenote stond ook een getal, voegde hij eraan toe, en ik kon natuurlijk zelf wel bedenken welk getal dat was!

Eerlijk gezegd houd ik niet zo van wiskundige uitdagingen op feestjes, maar een pas getrouwde vriend laat je natuurlijk niet in de steek. En een poosje later wist ik het: natuurlijk, de bruid heeft het getal 284 in haar ring staan! Nou moet ik toegeven dat ik dat niet ter plekke berekend had; blijkbaar ken ik meer getallenfeitjes dan ik dacht.

Want wat is er zo bijzonder aan de getallen 220 en 284? Het zijn bevriende getallen. Dat ze zo heten is niet een nieuwerwetse poging om getallen menselijker en hipper te maken dan men ze doorgaans vindt, de Pythagoreeërs kenden dit koppel al en spraken erover in termen van vriendschap. Een uitspraak die aan Pythagoras is toegeschreven luidt: “Wat is een vriend? Een ander ik, zoals gesymboliseerd wordt door de getallen 220 en 284.”

Juist... Maar waarom deze getallen? De delers van 220 zijn: 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110 en 220. Als je het getal 220 zelf niet meetelt en alle andere delers bij elkaar optelt, vind je het getal 284. Dat op zich is nog niet zo bijzonder. Maar als je hetzelfde doet voor 284, dan vind je 1 + 2 + 4 + 71 + 142 = 220! Daarom zijn de getallen 220 en 284 bevriend. Dit is het kleinste koppel bevriende getallen dat er bestaat. Andere voorbeelden zijn 1184 en 1210; 2620 en 2924; 5020 en 5564. Wiskundigen vermoeden dat er oneindig veel van dit soort paren bestaan, maar dat is niet bewezen.

In verscheidene oude Arabische manuscripten duikt een magische toepassing van deze getallenfeitjes op. Als je een goede relatie met iemand wil aanknopen, moet je de getallen 220 en 284 op een briefje schrijven. Dat briefje scheur je doormidden, het deel met 220 eet je op en het deel met 284 meng je ongemerkt door het eten van de ander. Succes gegarandeerd, zeker als je ook nog rekening houdt met een gunstige positie van Venus! En goed te combineren met het aanbieden van een zelfgekookt diner.

Deze column verscheen vandaag in de Volkskrant.

Mijn vriendin Cristel studeerde geschiedenis met als specialisatie achttiende-eeuwse dagboeken. Op feestjes belandt ze steevast naast iemand die werkelijk alles weet van de Peloponnesische oorlog. Als zo iemand hoort dat zij een historica is, dan verwacht hij dat ze daar uren met hem over kan praten. Cristel vindt het dan altijd een beetje gênant om toe te moeten geven dat zij helemaal niets weet van de Peloponnesische oorlog.

Als wiskundige kom je bijna nooit in zulke situaties, omdat de meeste mensen bij wiskunde niet verder komen dan de stelling van Pythagoras. Daarom was ik zo verbaasd toen iemand laatst op een borrel aan me vroeg hoe het zat met het vermoeden van Collatz.

Ik wist gelukkig wel wat het vermoeden van Collatz was. Het gaat over reeksen getallen. Je begint met een willekeurig geheel getal, groter dan nul. Als het getal even is, dan deel je het door twee. Als het getal oneven is, dan vermenigvuldig je het met drie en tel je er één bij op. Daarna herhaal je dit proces met de uitkomst, en opnieuw, en opnieuw.

Bijvoorbeeld:

6 -> 3 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1

of

13 -> 40 -> 20 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1.

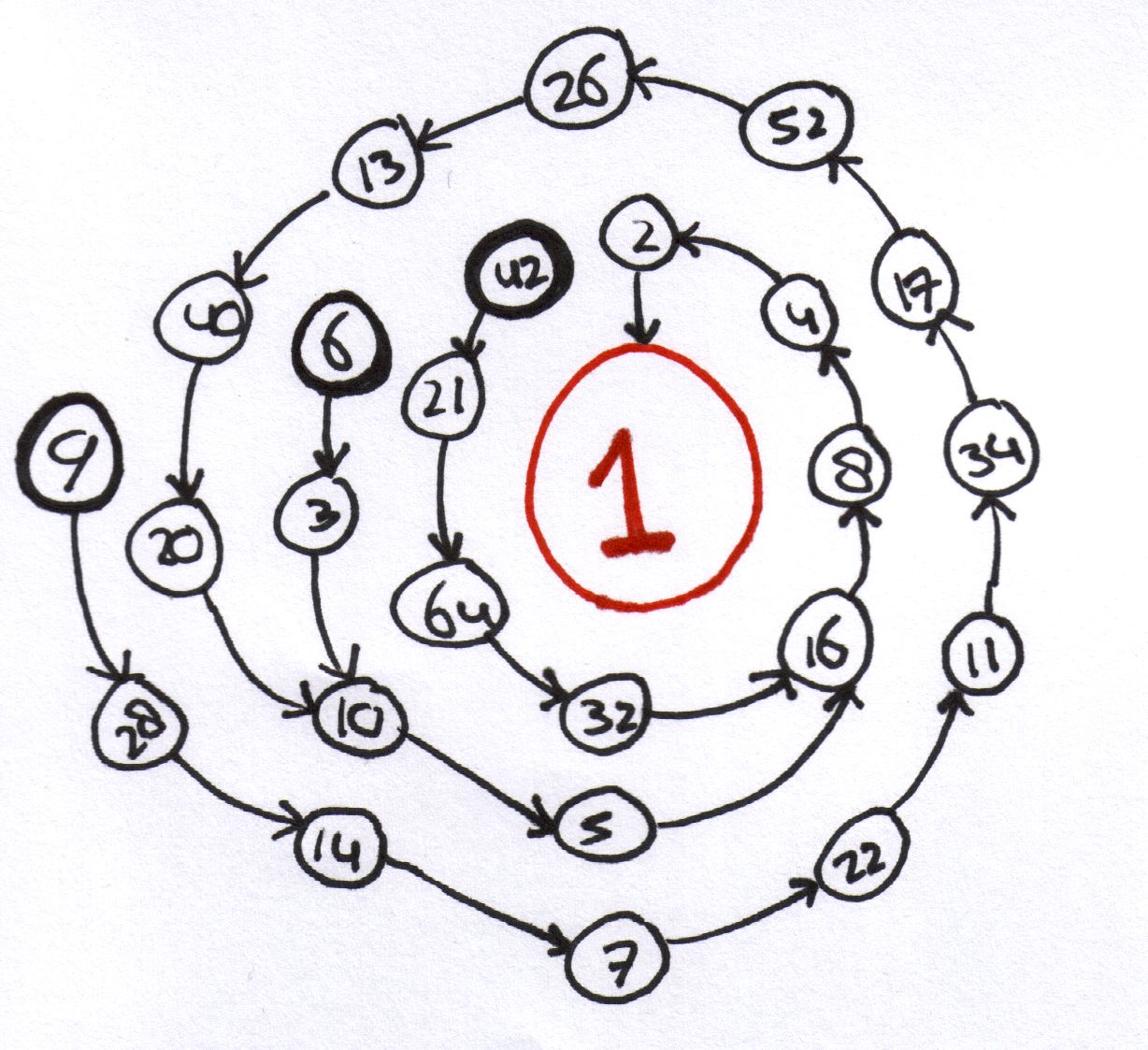
Het resultaat als je begint bij 6, 9 of 42.

Je stopt bij één, omdat je vanaf daar in een vicieuze cirkel belandt: één gaat immers naar vier en dan via twee weer terug naar één. Het vermoeden van Collatz is dat je altijd op één uitkomt, met welk getal je ook begint.

Probeer het zelf maar eens voor je lievelingsgetal. Als je getal kleiner is dan 10^18 dan kom je zeker op één uit, tot die grens is het vermoeden met de computer getest. Het aantal stappen kan behoorlijk groot worden: als je begint met een bescheiden 27 heb je bijvoorbeeld al 112 stappen nodig voor je bij 1 eindigt.

De meeste wiskundigen denken dat het vermoeden van Collatz waar is en dat je inderdaad voor elk getal bij één zult eindigen. Maar niemand heeft een bewijs. De in 1996 overleden wiskundige Paul Erdös verzuchtte volgens de overlevering dat de wiskunde nog niet klaar was voor dit soort moeilijke problemen. Voor de zekerheid loofde hij toch maar 500 dollar uit voor een oplossing. Die oplossing is er nog steeds niet.

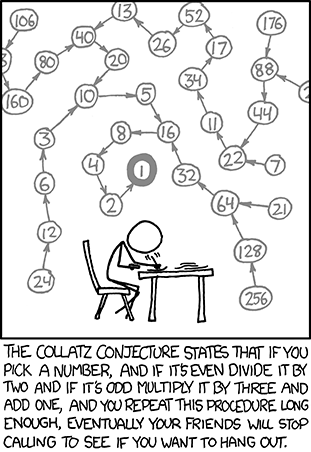
Dit alles vertelde ik op de borrel. De getallenvoorbeelden zocht ik snel op met mijn telefoon, iets wat ik ook van harte aanraad bij lastige vragen over Peloponnesische oorlogen. De vragensteller keek me wat teleurgesteld aan. Dus dit kunnen wiskundigen níet oplossen? Wat zitten jullie dan de hele dag achter jullie bureaus te doen? En wat kunnen jullie wel?

Het is misschien gênant om een vraag te krijgen over een onderwerp waarvan je nog nooit hebt gehoord. Maar het is nog veel gênanter om toe te moeten geven dat jij en je vakgenoten een ogenschijnlijk eenvoudig probleem niet kunnen oplossen.

Dit stuk staat vandaag in de Kennisbijlage van De Volkskrant. Helaas werkt de link in dat artikel niet meer, onderaan dit stuk staat de goede link naar meer informatie.

Morgen wordt wereldwijd pi-dag gevierd. Elk jaar verzamelen pi-liefhebbers zich in de derde maand op de veertiende dag (oftewel: 3,14) voor een feestje. Tijd om de grootste misverstanden over deze wiskundige constante recht te zetten.

1. Pi heeft iets te maken met de stelling van Pythagoras.
In de kerstuitzending van Bananasplit kwam pi ter sprake. Danny de Munck gaf onmiddellijk toe dat hij niets wist van wiskunde. Naast hem zat Nance, zij had ook geen wiskundeknobbel, maar “wist nog wel dat pi de stelling van Pythagoras is”. Helaas, pi en de stelling van Pythagoras zijn de twee dingen die de meeste mensen onthouden hebben van wiskunde, maar ze hebben niets met elkaar te maken. De stelling van Pythagoras gaat over driehoeken, terwijl pi van cirkels komt. Pi is de omtrek van een cirkel gedeeld door de diameter: ongeveer 3,14. Het maakt niet uit hoe groot of klein de cirkel is, de verhouding tussen omtrek en diameter is altijd precies pi. Daarnaast verschijnt pi ook op allerlei andere plaatsen: bijvoorbeeld in de verdeling van schoenmaten.

2. Pi is precies 3,14.
Pi begint als 3,14159 en daarna volgen nog oneindig veel cijfers. In die cijfers zit geen regelmaat. In de praktijk wordt daarom altijd een benadering van pi gebruikt. In de bijbel laat Solomo voor een tempel een bekken maken: “vijf el hoog, met een middellijn van tien el en een omtrek van dertig el”. Volgens deze tekst is pi dus gelijk aan 30/10 = 3, een eenvoudige benadering. Hoe nauwkeuriger de berekening, hoe meer decimalen er nodig zijn. Pi is niet te schrijven als een breuk, maar kan wel goed benaderd worden met breuken. Op school wordt vaak 22/7 (ongeveer 3,14285) gebruikt voor pi.

3. In de Amerikaanse wet staat dat pi gelijk is aan 3.
Het is een vaak voorkomend misverstand dat een bijbelvaste Amerikaanse staat in de wet heeft vastgelegd dat pi drie is. Zoiets is nooit gebeurd of zelfs maar voorgesteld. Wel is in 1897 in Indiana een merkwaardig wetsvoorstel ingediend door een amateurwiskundige. Hij wilde pi anders definiëren om berekeningen makkelijker te maken. In zijn voorstel waren allerlei verschillende waarden voor pi te vinden, variërend van 3,2 tot 4(!). Het voorstel werd in eerste instantie unaniem aangenomen, maar het sneuvelde alsnog in de senaat. Niet omdat de senaatsleden vonden dat er iets mis was met de theorie, maar omdat ze dachten dat pi geen zaak van wetgeving was.

4. In pi zitten geheime boodschappen verstopt.
Het zoeken naar gecodeerde boodschappen in de oneindige reeks decimalen van pi is een populaire hobby. Door de cijfers om te zetten naar letters kun je zinnen als “God bestaat” in de decimalen ontdekken. Het probleem is dat wiskundigen vermoeden dat elk rijtje cijfers uiteindelijk een keer in de decimalen van pi voorkomt, dus dan zou ook de zin “God bestaat niet” vanzelf een keer in de decimalen opduiken, net als de integrale tekst van Hamlet of de Volkskrant van vandaag. Voor wie het moeilijk te geloven vindt dat in één getal alle mogelijke teksten zijn gecodeerd: er is een getal waarvan we dit zeker weten dat alle mogelijke codes er instaan. Dat is de contante van Champernowne: 0,12345678910111213141516... enzovoorts. Niets magisch aan dus.

5. Het is belangrijk om pi zo ver mogelijk uit te rekenen.
Al eeuwenlang is het een sport om zoveel mogelijk decimalen van pi uit te rekenen. Omdat het er oneindig veel zijn, valt het record steeds weer te verbeteren. Zhu Chongzi berekende bijvoorbeeld rond het jaar 500 al dat pi tussen 3,1415926 en 3,1415927 ligt. Op dit moment staat het record op 2,7 biljoen cijfers. Om een indruk te geven hoe belachelijk veel cijfers dit zijn: als je deze 2,7 biljoen cijfers gaat opzeggen (zeg één per seconde), dan duurt dat 85.616 jaar. Voor de meeste berekeningen zijn echter een stuk of tien cijfers na de komma ruim voldoende en niemand heeft meer dan duizend cijfers nodig.

Dat de records toch steeds sneuvelen heeft twee redenen. Allereerst hebben snelle rekenmethodes allerlei andere toepassingen, het uitrekenen van pi is niet meer dan een mooie test. Bovendien raakt het uitrekenen van zoveel mogelijk decimalen voor sommige mensen een obsessie. Zelfs Isaac Newton raakte in de ban van pi en schreef in 1666: “Ik schaam me om te vertellen tot hoeveel cijfers ik deze berekeningen heb uitgevoerd, toen ik niets anders te doen had.”

Tot en met 28 maart hangen de eerste miljoen decimalen van pi in de Centrale Bibiliotheek Rotterdam als onderdeel van een expositie over de geschiedenis van pi. Morgen wordt tussen 13.00 en 17.00 uur pi-dag gevierd met lezingen, wiskundige puzzels en pi-koekjes. De toegang is vrij. Adres: Bibliotheek Rotterdam, Hoogstraat 110, Rotterdam. Meer informatie op de site van de bibliotheek.

Een tijdje terug schreef ik een stukje over wat er gebeurt als je een touw strak om de aarde spant, er een meter touw bij doet en vervolgens het touw overal evenver optilt. Zie ook dit filmpje.

Lezers Robert Groenewold en Lon Boonen brachten een lange avond in de kroeg door om deze vraag op te lossen. Ze stuurden onderstaande oplossing in. Wij vertellen ze maar niet dat dit alles al lang op de site van KP Hart te vinden was...

Onlangs spanden de wiskundemeisjes een touw strak om de aarde om het vervolgens een meter langer te maken en aan te tonen dat zelfs een lineair verband (tussen straal en omtrek) contra-intuïtief kan zijn. Aangezien allle moeite reeds gedaan is om genoemd touw te spannen wilden wij, twee natuurkundejongens, dat touw een alternatieve bestemming geven.
Wanneer we een touw strak rond de aarde spannen, één meter touw toevoegen en het geheel aan een spijkertje ophangen, wat is dan de afstand tussen de aarde en het spijkertje? Past de Domtoren er onder?

De oplossing kostte ons een avond in (het helaas ter ziele gegane) Ledig Erf in Utrecht. En ettelijke bierviltjes. Deels was dit te wijten aan het feit dat we (schaam, schaam) de Taylor-reeks opnieuw moesten ontdekken.

Read the rest of this entry »

Het is weer oktober, dus Oktober Kennismaand is van start gegaan! De hele maand worden overal in het land activiteiten georganiseerd waarbij je kennis kunt maken met de wereld van wetenschap en techniek. Het thema is: reis naar het onbekende. Want, volgens de website:

De reis van Darwin, de reizen van ruimterobots, de speurtocht via telescopen, de ontwikkeling van de snaartheorie, de zoektocht naar het Higgsdeeltje, het onderzoeken van de relatie tussen DNA en eiwitten, de fabricage van steeds kleinere structuren (nanotechnologie), quantumcomputers, energietechnologie, mobiliteitsonderzoek, het in kaart brengen van de menselijke geest, leven in de kosmos, natuurlijke systemen, klimaatsverandering, robotics… Allemaal zijn het reizen naar het onbekende.

Hieronder staan wat voorbeelden van grote activiteiten waar je vast wel wiskunde tegenkomt. Het hele programma per provincie kun je hier vinden. Er staat veel leuks bij!

• zondag 4 oktober: Publieksdag TU/e
• zaterdag 10 oktober: Science Park Amsterdam Open Dag 2009 - Centrum Wiskunde & Informatica (CWI)

  Trek rond door de verrassende wereld van wiskunde en informatica bij het Centrum Wiskunde & Informatica (CWI)! Reis naar de zon op aarde in een minicollege over kernfusie en wiskunde, of hoor hoe reuzenbliksems hoog boven de wolken ontstaan. Dwaal rond over de puzzelmarkt van Vierkant voor Wiskunde, laat je meenemen door Pythagoras - wiskunde voor jongeren. Knutsel in de Pretlabs en laat je verleiden door Arabesk wiskundepuzzels.

• zondag 18 oktober: Wetenschapsdag Universiteit Leiden

  De reis van Darwin, de reizen van ruimterobots, de speurtocht via telescopen, de ontwikkeling van de snaartheorie, de zoektocht naar het Higgsdeeltje, het onderzoeken van de relatie tussen DNA en eiwitten, de fabricage van steeds kleinere structuren (nanotechnologie), quantumcomputers, energietechnologie, mobiliteitsonderzoek, het in kaart brengen de menselijke geest, leven in de kosmos, natuurlijke systemen, klimaatsverandering, robotics… het zijn allemaal reizen naar het onbekende. Tijdens de Wetenschapsdag op zondag 18 oktober 2009 nemen Leidse musea en instituten en de Universiteit Leiden je mee op reis. Ook daar zullen Pythagoras en de puzzelmarkt van Vierkant voor Wiskunde aanwezig zijn.