Internetbureau Rotterdam 
Dit bericht is geplaatst op woensdag 22 maart 2006 om 19:54 in categorieën Algemeen. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Het vermoeden van Goldbach (2)
In Algemeen, door wiskundemeisjes
Sidney Cadot is geen wiskundemeisje, maar zijn reactie op het Goldbach stuk van afgelopen zaterdag is een eigen post waard. Hij stuurde twee plaatjes die hij lang geleden maakte en schreef:
``Ik was destijds eerstejaars informatica en toen kwam ooit het vermoeden van Goldbach aan de orde. Uiteraard sloeg ik aan het rekenen - wat ik bekeek was het aantal verschillende manieren g(k) waarop een even getal k te schrijven is als som van twee priemgetallen. Het vermoeden is natuurlijk dat g(k) > 0 voor alle k even, k > 2.
Het grappige is dat de grafiek daarvan een nogal bizarre structuur heeft (zie hieronder)."
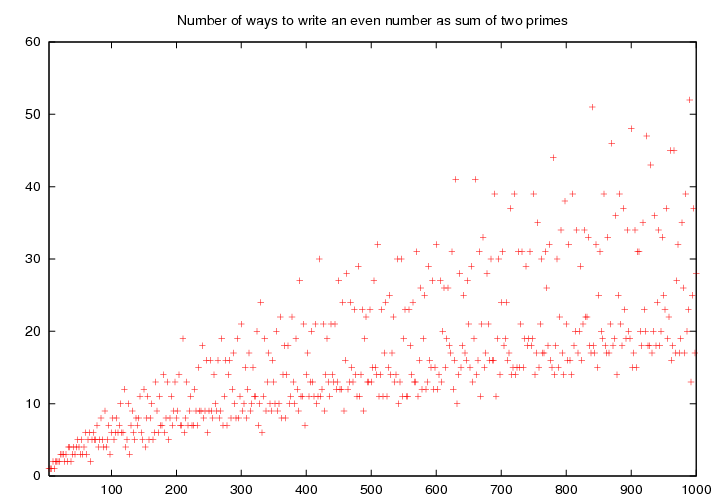
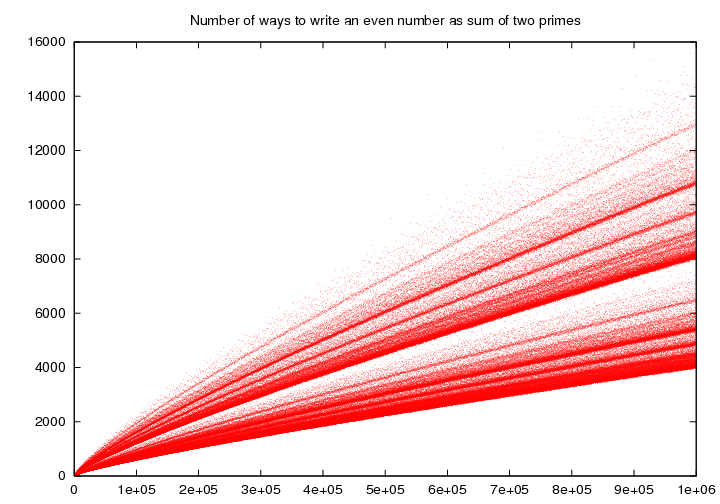
Sidney gaat verder: ``... Aan de onderste grafiek kun je zien dat het vermoeden wel waar zal zijn, maar dat is zeker niet voldoende voor jullie? ;-) Ik heb geen idee waar de band-structuur in de tweede grafiek vandaan komt (je kunt het ook al zien in de eerste grafiek trouwens). Nogal vreemd, niet dan?"
Degene in die de comments het vermoeden als eerste werkelijk bewijst (en dan dus ook echt voor ALLE even getallen groter dan 2, Sidney) krijgt van mij een Mars.
(Ionica)
