Dit bericht is geplaatst op donderdag 29 juni 2006 om 22:54 in categorieën Algemeen, Nieuws. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
De 290 stelling
In Algemeen,Nieuws, door wiskundemeisjes
Sommen van kwadraten
Een bekende stelling uit de getaltheorie vertelt ons dat ieder positief geheel getal te schrijven is als een som van 4 kwadraten. Deze stelling is in 1770 door Lagrange bewezen. Het begin van het lijstje ziet er als volgt uit.
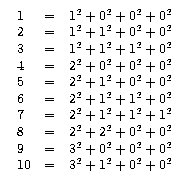
Een voor de hand liggende vraag is de volgende: zijn er nog meer van dit soort uitdrukkingen die alle positieve gehele getallen representeren en hoe kun je zien of een bepaalde uitdrukking dat doet?
Gehele positief-definiete kwadratische vormen
De 290 stelling geeft een verrassend antwoord op deze vraag: als je van een bepaald soort uitdrukking al weet dat hij een lijstje van 29 getallen representeert, dan weet je meteen dat hij alle positieve gehele getallen representeert! Maar eerst moeten we natuurlijk bedenken wat er in de vraag bedoeld wordt met "dit soort uitdrukkingen". Een mogelijk antwoord is: gehele positief-definiete kwadratische vormen. Dat is een hele mond vol, dus laten we per woord bekijken wat dat nou precies voor vormen zijn.
Voorbeelden van kwadratische vormen zijn:
x2 + y2,
x2 + y2 + z2 + u2,
1/2 xz,
x2 - 4z2 en
x2 + y2 + z2 - 14xz + 5yz.
Een kwadratische vorm is een som van termen die allemaal bestaan uit óf het kwadraat van een variabele, óf het product van twee variabelen, met een getal ervoor. De volgende uitdrukkingen zijn dus géén kwadratische vormen:
x2 - 2x,
x2 + 4 en
xy - 5xyz.
Merk op dat als je voor alle variabelen die voorkomen 0 invult, dat er dan altijd 0 uitkomt, wat je kwadratische vorm ook is!
Een gehele kwadratische vorm is een kwadratische vorm waarbij de getallen die voor de variabelen staan gehele getallen zijn.
Nu zijn we bij het laatste woord beland: positief-definiet. Een gehele kwadratische vorm noemen we positief-definiet in het volgende geval: als je gehele getallen invult, komt er altijd een getal groter dan 0 uit, behalve als je voor alle variabelen 0 invult, dan komt er 0 uit. De vorm x2 + y2 is dus inderdaad positief-definiet, want als x of y ongelijk aan 0 is, dan is x2 + y2 groter dan 0. Zo is het ook makkelijk te zien dat x2 + y2 + z2 + u2 positief-definiet is. De vorm x2 - 4z2 is niet positief-definiet: als je bijvoorbeeld x=1 en z=1 invult komt er -3 uit. Ook x2 + y2 + z2 - 14xz + 5yz is niet positief-definiet, want deze vorm representeert -12 (neem x=1, y=0 en z=1).
De 290 stelling
Nu zijn we ver genoeg om de mededeling die de 290 stelling doet te kunnen begrijpen. Deze stelling werd onlangs bewezen door Manjul Bhargava en Jonathan P. Hanke. Het is een beetje een bizarre stelling, met 29 getallen die volledig uit de lucht lijken te vallen. De 290 stelling luidt als volgt.
Als een gehele positief-definiete kwadratische vorm de getallen 1, 2, 3, 5, 6, 7, 10, 13, 14, 15, 17, 19, 21, 22, 23, 26, 29, 30, 31, 34, 35, 37, 42, 58, 93, 110, 145, 203 en 290 (vandaar de naam!) allemaal representeert, dan representeert de vorm alle positieve gehele getallen!
De stelling zegt dus iets heel sterks: als je een gehele positief-definiete kwadratische vorm hebt, dan hoef je maar voor een eindig aantal, namelijk 29, getallen te controleren of ze door deze vorm gerepresenteerd worden. Als dat het geval is, dan weet je meteen dat alle positieve gehele getallen er uit kunnen komen! Je hoeft dus niet voor alle getallen na te gaan of ze gerepresenteerd kunnen worden, en dat is maar goed ook, want dan zou je dat voor een oneindig aantal getallen moeten doen...
En er is nog iets leuks aan de hand: Bhargava en Hanke zijn er zelfs in geslaagd om voor elk van deze 29 getallen een gehele positief-definiete kwadratische vorm te vinden die alle positieve gehele getallen representeert, behalve dat ene getal! Dat betekent dat uit dat lijstje van 29 ook echt geen enkel getal meer weg te laten valt.
Hier kun je nog meer lezen over Manjul Bhargava en de 290 stelling (in het Engels).
(Jeanine)
 Internetbureau Rotterdam
Internetbureau Rotterdam 
