Dit bericht is geplaatst op zaterdag 1 juli 2006 om 08:06 in categorieën Algemeen. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Mijn favoriete formule
In Algemeen, door wiskundemeisjes
Wat doe je als iemand vraagt wat je favoriete formule is: welke formule eigenlijk iedereen zou moeten kennen? Zeg je:
a) Alle formules zijn gelijk, maar sommigen zijn meer gelijk dan anderen.
b) e π i = -1 natuurlijk!
c) Nou, eigenlijk is er geen ultieme formule die iedereen moet kennen. Wiskunde is zo veel meer dan formules. Logisch denken en bewijzen vind ik veel mooier dan formules.
d) De Formule 1.
Ik probeerde eerst antwoord c). Maar degene aan de andere kant van de lijn gaf geen krimp en hield vol. Dus eindigde ik met antwoord b). Want dat is toch wel mijn favoriete formule. Waarom?
Mijn favoriet: e π i = -1
Laten we eens rechts van het =-teken beginnen, daar staat -1. Dat is makkelijk, dat kennen we allemaal. Maar vroeger was het helemaal niet zo vanzelfsprekend om negatieve getallen te gebruiken. Heb je wel eens -2 appels gezien? Het duurde even voor mensen inzagen dat als je geen appels had maar wel nog 2 appels aan iemand moest geven, je best kon zeggen dat je -2 appels had.
En wat staat er allemaal links van het =-teken? We zien e, π en i. Pi (π voor vrienden) ≈ 3.14159 en het is de bekende verhouding tussen de diameter van een cirkel en zijn omtrek. Wat zijn die andere twee letters e en i?
De prachtige constante e
e ≈ 2.71828 is een constante met een bijzondere eigenschap. Als je de grafiek van ex tekent, dan heeft deze grafiek in elk punt precies dezelfde helling als de waarde van de functie. Hieronder zie je links de grafiek van ex en rechts de grafiek van zijn helling:
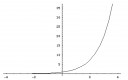

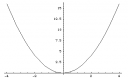
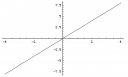
Even ter vergelijking, hieronder links een parabool en rechts zijn helling:
Deze constante e duikt op allerlei gekke plaatsen op: bij lootjes trekken voor Sinterklaas bijvoorbeeld. De kans dat niemand zichzelf trekt is 1/e voor grote groepen.
De imaginaire constante i
Op de middelbare school leerde ik dat de wortel uit een negatief getal niet bestaat. Ik voelde me enorm bedrogen toen ze op de universiteit doodleuk zeiden dat i2 = -1. Dat kon toch helemaal niet? Want 1 x 1 = 1 en -1 x -1 = 1. Wiskundigen trekken zich daar niks van aan en definiëren i domweg als het getal waarvoor wel geldt dat i x i = -1. Vervolgens rekenen ze vrolijk met die imaginaire (denkbeeldige) i en het leuke is, dat je daardoor allerlei mooie berekeningen kan maken, waar we ook in de echte wereld iets aan hebben. Eigenlijk verschilt zo'n imaginaire constante helemaal niet zo veel van een negatief getal, ook die zie je niet om je heen, maar kan je wel heel goed gebruiken.
Terug naar de fomule... e π i = -1
Waarom is dit nu mijn favoriete formule? Omdat je links allerlei moeilijke dingen ziet, die ineens gelijk blijken te zijn aan iets heel eenvoudigs. Dat is wat wiskundigen leuk vinden, moeilijke dingen makkelijk maken. En soms lijkt dat wel een beetje op een wonder...
(Ionica)
 Internetbureau Rotterdam
Internetbureau Rotterdam 
