Dit bericht is geplaatst op woensdag 19 juli 2006 om 20:36 in categorieën Algemeen, Geschiedenis. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Khinchin en kettingbreuken
In Algemeen,Geschiedenis, door wiskundemeisjes

Vandaag is het precies 112 jaar geleden dat Aleksandr Yakovlevich Khinchin in Rusland werd geboren. Hij bewees een mooie stelling over kettingbreuken en toevallig houd ik heel erg van kettingbreuken, dus de verjaardag van Khinchin (al is de beste man inmiddels overleden) leek me een mooie aanleiding om eens iets over kettingbreuken te vertellen.
Een kettingbreuk heeft niets te maken met fietskettingen: het is een breuk in een breuk, in een breuk, enzovoorts. Je hebt verschillende vormen kettingbreuken, maar een 'gewone' kettingbreuk ziet er zo uit:
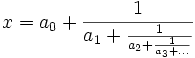
De coefficienten ai zijn gehele positieve getallen, alleen a0 mag negatief zijn als x dat ook is. Je vindt die getallen ai door steeds het algoritme van Euclides te gebruiken (waarmee je de grootste gemene deler van twee getallen kan bepalen).
Benaderingen (met een voorbeeld om het duidelijk te maken)
Het leuke is dat je elk getal x als een kettingbreuk kan schrijven. En als dat getal x zelf niet als een gewone breuk te schrijven is (dat is bijvoorbeeld waar voor pi, wortel 2 en de gulden snede), dan gaat die kettingbreuk oneindig lang door. Je kan zo'n oneindige lange kettingbreuk dan afkappen om een benadering te vinden voor je getal x en dit geeft een reeks steeds beter wordende benaderingen.
Zoals de tussenkop al zegt, zal ik het proberen duidelijk te maken met een voorbeeld. Laten we eens kijken naar benaderingen voor pi ≈ 3.14159. De kettingbreuk voor pi begint als volgt:
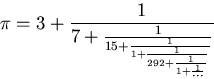
De eerste afgekapte kettingbreukbenadering voor pi is 3, wat niet zo'n goede benadering is. De tweede benadering is 22/7 ≈ 3.14285. Deze benadering wordt op school vaak gebruikt en heeft de eerste twee decimalen van pi al goed. De volgende benadering is 333/106 ≈ 3.14151 en die doet de derde en vierde decimaal ook goed. Met elke volgende stap worden de benaderingen een stukje beter.
Voor ik het resultaat van Khinchin geef, nog een leuk feitje over kettingbreuken. Als je de kettingbreuk voor de gulden snede berekent, dan krijg je een kettingbreuk met alleen maar enen:
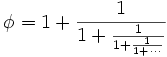
Daardoor is de gulden snede het moeilijkste getal om te benaderen met breuken. Zou dat de reden zijn dat mensen zo van deze verhouding houden?
De constante van Khinchin
Aleksandr Khinchin bewees dat voor bijna elk getal x geldt dat het meetkundige gemiddelde van de getallen ai in zijn kettingbreuk gelijk is aan een constante:
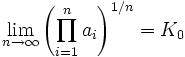
Die constante Ko heet de constante van Khinchin en is ongeveer gelijk aan 2.68545. Dat 'bijna elk getal' klinkt misschien een beetje vaag, maar voor wiskundigen is dat een heel helder gedefinieerd begrip. En dat zoiets als hierboven geldt voor bijna elke x is echt een mooi resultaat.
Dit stukje is te kort om echt veel te vertellen, maar wie meer wil weten over kettingbreuken kan eens kijken op Continued Fractions...an introduction.
In mijn eigen onderzoek werk ik trouwens aan multidimensionale kettingbreuken. Het probleem is nu om niet één getal, maar een heel rijtje getallen tegelijk met breuken te benaderen. En daarbij wil je ook nog dat elke benaderingsbreuk dezelfde noemer heeft. Waarom dat handig is en hoe je die schattingen kunt vinden, zal ik vertellen in een latere post!
(Ionica)
 Internetbureau Rotterdam
Internetbureau Rotterdam 
