Wiskundemeisjes

Ochtendprobleem vrijdag

Zet de getallen 1 t/m 16 in de zestien vakjes van onderstaande figuur aan de hand van de volgende aanwijzingen:

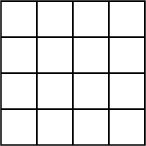
* Elk getal komt precies eenmaal voor.
* Het getal 14 staat in een lagere rij dan het getal 1.
* Het getal 9 staat direct boven het getal 4.
* Alle getallen in de eerste kolom zijn priemgetallen.
* De som van alle getallen op een van de diagonalen is 37.
* Op twee hoekpunten komt een veelvoud van vijf te staan.
* Het getal 16 staat meer naar links en lager dan het getal 2.
* Het getal 7 staat niet in een rij waar het getal 6 of het getal 8 al staat.
* Het getal 8 staat niet direct onder, maar wel recht onder het getal 15.
* Het product van de getallen uit de vakjes die niet aan de rand liggen is 240.
* Als je de getallen van één kolom bij elkaar optelt, dan komt er bij elke kolom hetzelfde getal uit.
* Er zijn geen vakjes waarbij het getal in het horizontaal aangrenzende vakje (links, of rechts) precies 1 verschilt met het getal in dat vakje.

(Jeanine)

9 reacties op “Ochtendprobleem vrijdag”

1. Steven:
   vrijdag 18 augustus 2006 om 15:14

   Na wat puzzelen en vooral veel wegstrepen hieronder de oplossing (volgens mij dan) van het laatste ochtendprobleem:
   07 09 12 15
   13 04 06 01
   03 05 02 08
   11 16 14 10

2. Dennis:
   vrijdag 18 augustus 2006 om 16:26

   Ik heb hetzelfde antwoord. Het eerste getal dat ik vond was 8.

3. Michiel Kosters:
   vrijdag 18 augustus 2006 om 19:33

   Wij (Ariyan en ik) vonden dezelfde als Steven:
   7 9 12 15
   13 4 6 1
   3 5 2 8
   11 16 14 10
   We begonnen met het factoriseren van 240.

4. anoniempje:
   maandag 21 augustus 2006 om 10:20

   Ik vond ook hetzelfde, maar ik ben begonnen met het feit dat iedere kolom dezelfde som heeft en ieder element uniek is, dan heb je al alle priemgetallen in je linkerkolom en erna kan je makkelijk de 2 andere hoekpunten vinden (15 en 10) etc...

5. Joris Weimar:
   dinsdag 22 augustus 2006 om 16:23

   Leuker misschien is te kijken of dit de unieke oplossing is en in dat geval hoeveel eisen je weg kan laten zonder dat het meer oplossingen toelaat :)

6. Jitske:
   dinsdag 22 augustus 2006 om 20:38

   Dit was volgens mij een ochtendprobleem van woensdag... Ik heb hem namelijk opgelost en ik kan met zekerheid zeggen dat ik op de vrijdag niet wakker genoeg was om nog maar één ochtendprobleem op te lossen...

   Kamp was natuurlijk wel super!

   Groetjes, Jitske

7. Jeanine:
   woensdag 23 augustus 2006 om 10:58

   @ Jitske: Inderdaad, de dagen van de ochtendproblemen op kamp kloppen niet met de dagen op de wiskundemeisjes. Soms stonden er twee erg leuke problemen op een dag, en op maandag waren er op kamp uberhaupt nog geen ochtendproblemen. Bovendien: op de wiskundemeisjes liepen de problemen een beetje op in moeilijkheidsgraad, terwijl we ze op kamp soms een beetje lieten aflopen, om voor de hand liggende redenen! ;-)

   En het kamp was inderdaad echt leuk! :-)

8. hnhiuoj:
   zondag 10 juni 2007 om 16:30

   nurds
   nurds
   nurds
   nurds
   nurds
   nurds
   nurds
   nurds
   nurds
   nurds

9. Arno van Asseldonk:
   zondag 10 juni 2007 om 17:54

   @hnhiuoj: Als je dan toch neerbuigend over mensen meent te moeten doen die toevallig sterk geïnteresseerd zijn in wiskunde, neem dan in ieder geval even de moeite om nerds op de juiste manier te spellen.

Plaats een reactie