Wiskundemeisjes

Kun je vermenigvuldigen, vermenigvuldig mee!

Een tijdje terug kregen we twee emails over hetzelfde filmpje binnen. Zowel Martin als Arjan stuurden ons een link naar Math Lesson: A new way to multiply.

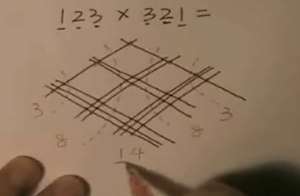
De methode die gebruikt wordt is helemaal niet zo nieuw, maar het ziet er mooi uit én het is leuk om te bedenken waarom dit werkt.

(Ionica)

15 reacties op “Kun je vermenigvuldigen, vermenigvuldig mee!”

1. fred schalekamp:
   dinsdag 19 december 2006 om 12:38

   Jammer dat het opschrijvenn van het eindresultaat van links naar rechts gaat.
   Als er door het 'onthouden' nogmaals moet worden 'onthouden' gaat het van rechts naar links in één keer goed.

2. fred schalekamp:
   dinsdag 19 december 2006 om 12:39

   Probeer eens 999*999!
   Je telt je rot.

3. Ionica:
   dinsdag 19 december 2006 om 13:42

   Je moet natuurlijk altjd de handigste methode kiezen! Ik zou 999 * 999 persoonlijk uitrekenen als 1000 * 999 - 999...

4. Arjen:
   dinsdag 19 december 2006 om 14:51

   Ik zou gaan voor 1000 * 1000 - 2 * 1000 + 1.

5. Vincent:
   dinsdag 19 december 2006 om 17:14

   Ik zou 999 eerst ontbinden in priemfactoren....

6. Michiel Kosters:
   dinsdag 19 december 2006 om 17:41

   leuke methode

7. Arjan Eising:
   dinsdag 19 december 2006 om 18:28

   Ik dacht al, waar blijft het filmpje :)

8. Frank Tabak:
   dinsdag 19 december 2006 om 19:33

   Ik pak gewoon een rekenmachine....

   Maar wel leuke methode!

9. Matthijs:
   woensdag 20 december 2006 om 11:36

   Heb ik even indruk gemaakt als niet-wiskundige bij mijn nog-minder-wiskundige vrienden.

   Ik kon het zelfs uitleggen, hoe trots zal mijn wiskundeleraar wel niet zijn!

10. MarijkeV:
    donderdag 21 december 2006 om 10:27

    Misschien een 'domme' vraag, maar wat doe je in deze methode met een getal eindigend op nul. Hoe vermenigvuldig je bijvoorbeeld 200 met 70?

11. MarijkeV:
    donderdag 21 december 2006 om 10:30

    En wat met een getal waar er een nul in het midden staat? Bijvoorbeeld 101x2?

12. Tim:
    donderdag 21 december 2006 om 16:48

    Je moet wel zien wat de eenheden, tientallen, honderdtallen, enz. zijn. Daarom moet je dus ook een nul zien. Je kunt op die plaats een groter gat laten, maar bijv. met een stippellijn zou je dat ook makkelijk (en duidelijk) aan kunnen geven.

13. harriet:
    donderdag 6 december 2007 om 14:49

    Waar komt deze methode vandaan?
    is er iemand die hem bedacht heeft ofzo?

14. harriet:
    donderdag 6 december 2007 om 14:50

    Waar kwam deze methode vandaan?
    is er iemand die hem bedacht heeft ofzo?

15. hoi:
    vrijdag 13 juni 2008 om 19:50

    HEEY JE HEBT EEN PROBLEEM ALS JE DOET BIJV. 1030*12

    WANT: ER ZIT EEN NUL TUSSEN DE 1 EN DE 3

    PROBEER DAT MAAR EENS UIT T E REKEN

    DUS... DIE MANIER IS TOG NIET WATERDICHT

    maar wel heeeeel goed!!!! :D
    want als je een proefwerk hebt xD en je vergeet je reken machine kan je deze truc nog gebruiken :p

Plaats een reactie