Dit bericht is geplaatst op maandag 15 januari 2007 om 14:03 in categorieën Geschiedenis, Nieuws. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Vergeten wortels
In Geschiedenis,Nieuws, door wiskundemeisjes
Afgelopen vrijdag gaf Jan Hogendijk in Utrecht zijn oratie Vergeten Wortels. De oratie was een reis door diverse culturen die aan de wiskunde hebben bijgedragen. Hierbij een korte samenvatting van zijn toespraak.
Al 3700 jaar geleden hielden de Babyloniërs zich bezig met het volgende probleem. Hoe bereken je de lengte van de diagonaal van een vierkant als de lengte van de zijde bekend is? Op het onderstaande kleitablet (YBC 7289) kun je de vraag en oplossing zien als de zijde lengte 30 heeft.

Hier zie je een duidelijker getekende versie en eentje waarin de cijfers in moderne cijfers getranscribeerd zijn.
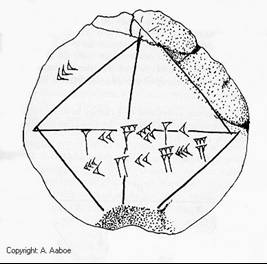
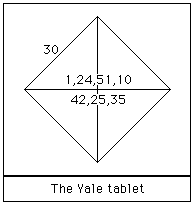
Jan Hogendijk onderstreept het belang van het gebruik van dit soort echte bronnen in het onderwijs. Studenten kunnen dan zelf een interpretatie uitwerken, of zelf uitvinden hoe het Babylonische getalsysteem werkt aan de hand van een kleitablet.
Ook in het werk Meno van Plato komt dit probleem voor. Socrates stelt aan een slaaf de juiste vragen en de slaaf ziet in dat het vierkant op de diagonaal een oppervlakte heeft die twee keer zo groot is als die van het vierkant op een zijde:
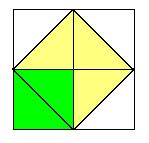
In moderne termen zeggen we: de diagnoaal is even lang als √2 keer de lengte van de zijde. De cijfers op het Babylonische kleitablet (42 25 35 en 1 24 51 10) geven de oplossing van het probleem. Naar moderne getallen vertaald stellen deze getallen namelijk voor:
42 25 35 = 42 + 25/60 + 35/3600 en dat is ongeveer 42,426389
en
1 24 51 10 = 1 + 24/60 + 51/3600 + 10/216000, wat ongeveer gelijk is aan 1,4142129.
Het eerste getal is ongeveer gelijk aan 30 × √2, het tweede aan √2. Die benadering is zo nauwkeurig, dat we kunnen uitsluiten dat de Babyloniërs die door metingen hebben kunnen vinden, zo precies kun je helemaal niet meten. Ze moeten dus een methode hebben gehad om dit getal te benaderen.
In de achtste eeuw ontstond in Bagdad een grote belangstelling voor de wiskunde. Daar kende men de Griekse en Indiase wiskunde en er werd veel nieuwe wiskunde ontwikkeld. Ook Al-Khwarizmi, die rond 800 leefde in het grote Islamitische rijk van die tijd, benaderde √2. Hij gebruikte hiervoor een Indiase methode. Op Kennislink kun je een artikel van Jan Hogendijk lezen over Al-Khwarizmi.
Pas veel later, vanaf de renaissance, werd ook in West-Europa wiskunde van betekenis ontwikkeld. Een bekende Nederlandse wiskundige is Ludolph van Ceulen. In zijn boek Van den Cirkel berekent hij bijvoorbeeld een benadering van π. Daarvoor heeft hij een benadering van √2 nodig, die hij berekent met de Indiase methode van Al-Khwarizmi.
Van Ceulen werd lang beschouwd als een doorzetter zonder veel origineel vermogen. Dat is onterecht: hij deed veel moeilijkere dingen dan π benaderen. De ontwikkelingen in de wiskunde moeten bovendien de 17de eeuwse landmeetkunde essentieel veranderd hebben, maar daar is nog veel niet over bekend. Jan Hogendijk pleit hier voor een rol van de historicus van de wiskunde: hij moet en kan een bijdrage leveren aan de cultuurgeschiedenis.
Wat Jan Hogendijk fascinerend vindt, is hoe de wiskunde tijdloze en tijdgebonden elementen combineert. Bij tijdgebonden elementen kun je denken aan de context en aan toepassingen. Bovendien heeft hij veel bewondering voor de wiskundigen in oude culturen.

De titel Vergeten wortels is dan ook op twee manieren uit te leggen. Allereerst verwijst hij naar het worteltrekken zelf. Tegenwoordig leren leerlingen op school niet meer met de hand worteltrekken, ze gebruiken daar een rekenmachine voor. Hogendijk heeft een aantal studenten met de hand leren worteltrekken met de methode van Van Ceulen. Op die manier kun je meer inzicht krijgen in de wiskunde.
Maar Vergeten wortels verwijst natuurlijk ook naar de wortels van de wiskunde die liggen in culturen en perioden waar wij geen weet van hebben, zoals Babylon en India. Tussen de 6de en 10de eeuw was er bijna geen wiskunde te vinden in West-Europa, de Islamitische wiskundigen en astronomen waren de leermeesters van de Europeanen. Dat is een belangrijk inzicht voor deze tijd, vindt Jan Hogendijk.
Na de wortels gaat hij verder met de vruchten. De wiskunde is na 1600 enorm gegroeid: van een wetenschap van getal en ruimte werd ze de wetenschap van structuren in het algemeen. Veel moderne dingen als cd's en pinnen zijn onmogelijk zonder complexe wiskunde, maar dat is vaak moeilijk uit te leggen aan mensen met weinig wiskundige kennis. De geschiedenis van de wiskunde kan de wiskunde een menselijk gezicht geven, in de geschiedenis zijn bovendien toegankelijke toepassingen te vinden. Op die manier kan de geschiedenis van de wiskunde het wiskunde-onderwijs verlevendigen. Het is belangrijk het imago van de wiskunde te verbeteren.
Een andere vrucht van het onderzoeken van de geschiedenis van Islamitische wiskunde is dat we op die manier relaties met Islamitische landen kunnen verbeteren. Er is daar veel belangstelling voor hun eigen wetenschappelijke traditie, maar er is nog weinig aan onderzocht. Door samenwerking kunnen we wetenschappers en studenten van hier in contact brengen met de bevolking daar en met de originele bronnen, en de wetenschappers en studenten van daar met hun eigen wortels. Zo ontstaat meer begrip voor elkaar.
Jan, de wiskundemeisjes feliciteren je van harte met je benoeming en je prachtige oratie!
(Jeanine)
Aanpassing 17 januari: de volledige tekst staat nu online.
 Internetbureau Rotterdam
Internetbureau Rotterdam 
