Internetbureau Rotterdam 
Dit bericht is geplaatst op donderdag 22 maart 2007 om 16:38 in categorieën Algemeen, Nieuws. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Magisch vierkant
In Algemeen,Nieuws, door wiskundemeisjes
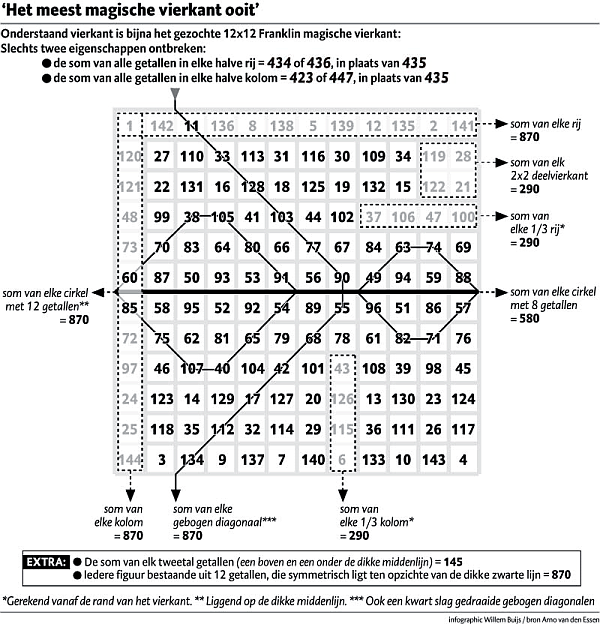
Drie scholieren hebben een heel bijzonder magisch vierkant gevonden, melden onder andere het Brabants dagblad en de NOS. Ze vonden het nadat ze aan een masterclass van Arno van den Essen hadden deelgenomen, op de Radboud Universiteit Nijmegen. Arno van den Essen schreef vorig jaar ook een boek over magische vierkanten. Jesse Hoekstra (17) en Willem Schilte (17) uit Nijmegen en Petra Alkema (15) uit Heeswijk-Dinther hebben het bijna-Franklin magische vierkant hierboven gemaakt.
In een magisch vierkant van n bij n staan de getallen 1 tot en met n2 en wel zodanig dat de som van de getallen in elke rij en elke kolom hetzelfde is. Het vierkant dat de drie scholieren gevonden hebben heeft nog veel meer mooie eigenschappen, zoals je in het plaatje zelf kunt zien. Leuk!
Als je meer wil weten over magische vierkanten: kijk eens op de Engelse wikipedia of lees meer over Franklins magische vierkanten op mathpages.
(Jeanine)
donderdag 5 april 2007 om 15:14
Beste Marco,
het heeft even geduurd maar mijn 16*16 vierkant is nu volledig in orde alle eigenschappen van Franklin gelden, de diagonalen zijn ok elke rij, elke kolom, elke gebogen diagonaal, elke cirkel van 16 hokjes,elk kruis van 16 hokjes elke waaier van 4 keer 4 hokjes ... heeft als som 2056 elk vierkant van 2 op2 heeft als som 514 de halve kolommen, rijen diagonalen hebben som 1028 cirkels en kruisen van 8 hokjes ook en de verdeling van de priemgetallen is behouden!!! Van den Essen was blijkbaar zeer geïnteresseerd en dus heb ik mijn nieuwe volledig magische vierkant nog eens doorgestuurd. als je het ook wil mag je me altijd een mailtje sturen (jordy.vanpoucke@ugent.be)
Mvg. Jordy
donderdag 5 april 2007 om 15:25
@ Jordy: wij zijn wel benieuwd! Kun je het ook even mailen naar mail@wiskundemeisjes.nl? Niet per se voor op de site, maar gewoon omdat we het zelf leuk vinden!
donderdag 5 april 2007 om 15:53
@Jordy: kunt u het ook naar mij sturen; darkiekurdo @ hotmail.com. Het lijkt mij erg interessant. Misschien is 'ie wel mooier dan die van die drie kinderen. ;) Bedankt!
donderdag 5 april 2007 om 21:33
@Jordy: Ook ik ben zeer benieuwd. Klinkt als een heel mooi magisch vierkant. Wil je het naar mij opsturen? (ik stuur je wel een mailtje met mijn adres) Hoe heb je het gemaakt? Met de hand of computer? Nog speciale trucs gebruikt?
vrijdag 6 april 2007 om 02:57
hoi Jordy,
Ik ben ook benieuwd naar je vierkant.
Maar wat bedoel je eigenlijk met een waaier van 4 keer 4 hokjes?
En wat versta je onder een kruis van 8 hokjes?
vrijdag 6 april 2007 om 14:11
Is moeilijk uit te leggen die waaier, ik kan hier geen figuurtjes plaatsen hé...
dat kruis is eenvoudig je neemt gewoon een vierkant van 4 op 4 hokjes en je schrapt daarin de cirkel bestaande uit 8 hokjes (die als som ook 1028 heeft) en dan blijft er een soort kruis over die als som 1028 heeft en samen is dit natuurlijk 2056 de som van elk 4 op 4 vierkant
Mvg. jordy
vrijdag 6 april 2007 om 14:16
Hey,
het is weldegelijk volledig met de hand gemaakt, ik heb gewoon gekeken naar verbanden tussen mijn kolommen en dan enkele permutaties doorgevoerd en zo bekwam ik mijn magische vierkant... ik heb het daarna wel op de computer gezet om het volledig te controleren maar de eerste schets was met pen en papier en ook een rekenmachine om niet alles uit het hoofd te moeten berekenen hé ;-)
Mvg. Jordy
zondag 8 april 2007 om 15:13
Hey Jordy,
als je naar die mensen verstuurd, moet je wel copyright zetten he. je weet maar nooit, andere kunnen met jou idee vandoor gaan ;p
maandag 9 april 2007 om 11:33
Ha die Jordy,
Ik heb nog geen tijd gehad om goed naar je vierkant te kijken, maar één ding is me wel opgevallen: Je noemt kruizen en cirkels alsof het bijzondere extra eigenschappen zijn die je met de hand na bent gegaan. De 2x2-blokjeseigenschap is echter zo bijzonder sterk dat veel andere figuren hiermee te maken zijn.
Bijvoorbeeld: Als je twee 2x2-blokjes naast elkaar zet, krijg je een 2x4-blok dat vaste som 2*514 heeft. Door twee 2x2-blokjes boven elkaar te zetten krijg je een 4x2-blok met ook som 2*514. Door een 2x4 en een 4x2 op elkaar te leggen krijg je een `plus' van 12 blokjes en als je de som neemt van de vakjes in de `plus', waarbij je de middelste 4 blokjes twee keer telt, dan krijg je dus altijd 4*514 als som. Maar die middelste 4 blokjes hebben vaste som 514, dus als je die er twee keer af haalt, dan krijg je een cirkel van 8 blokjes met vaste som 2*514. Op die manier kan je heel veel figuren maken van 4*n blokjes en een vaste som van n*514, zoals het kruis (4x4-blok met cirkel weggelaten). Die 2x2-eigenschap heeft nog meer mooie voordelen: je hoeft bijvoorbeeld maar 1 halve kolom/rij te checken om van alle evenwijdige halve kolommen/rijen te bewijzen dat ze som 1028 hebben en als je een rij en een kolomo invult, dan kan je de 2x2-blokjes gebruiken om de rest van het vierkant in te vullen!
dinsdag 10 april 2007 om 10:56
@ Arjen (#48): als meneer Arjen een paar minuten over heeft om eens te kijken naar het vierkant van onze scholieren en dat vergelijkt met die van mijn link dan kan hij zelf het volgende concluderen: 1) Spiegelen over een as heeft geen invloed op de magisch-heid van een magisch vierkant en mag dus "straffeloos" 2) Wisselen van gepaarde rijen/kolommen met dezelfde eigenschapen heeft geen invloed op de magisch-heid van een magisch vierkant en magmag ook "straffeloos".
In dit voorkomende geval worden twee dubbele rijen (namelijk rijen 5/6 en 7/8) uit het vierkant van de scholieren die samen dus beide dezelfde eigenschappen hebben gewisseld, ergo, dit mag dus ook straffeloos. Daardoor is het vierkant van de studenten "gewoon"een permutatie van die van mijn link.
Voor een kleine verklaring van dit laatste mbt deze rijen: elke hele set van 4 (beginnend dus bij getal 73) telt tot 290, elke gehele (dus enkel beginnend op oneven cellen) horizontaal set van 2 telt tot 143/147 (en vice verssa), ook de diaginalen in beide rijen tellen hetzelfde in de kolommen de 1e keer tot 160/130 de volgende tot 176/114 etc. Meer relevante eigenschappen zijn er niet omdat enkel deze eigenschappen bepalend zijn voor het Franklin magisch zijn van een vierkant. Dus als je beide verwisselt, verander je niets aan de magisch-heid van het vierkant.
E.e.a. geld daardoor dus niet voor de kolommen 5/6 en 7/8, die zijn namelijk niet "hetzelfde"genoeg. Horizontaal per set van twee wel (nl 144/146) maar diagonaal niet.
Het is trouwens om dezelfde reden ook mogelijk om rijen 3/4 met 9/10 te ruilen. En 1/2 met 11/12. Verder heb ik eea niet onderzocht, maar dit geeft dus om te starten al een leuk aantal permutaties van het vierkant.
dinsdag 10 april 2007 om 11:22
@Arthur: Nou, nou, we hoeven ook niet gelijk zo gepiqueerd te doen hoor.
Ik had inderdaad de tijd genomen om de vierkanten te vergelijken en mijn vorige comment beschrijft mijn observaties.
Jij en ik komen tot dezelfde conclusie ten aanzien van hoe de twee vierkanten verschillen. We merken ook beide op dat spiegelen in de diagonaal een vrij eenvoudige operatie is.
Jij zit geloof ik een beetje beter in de stof en kan dus eenvoudig inzien dat het wisselen van geschikte aangrenzende paren rijen of kolommen in dit vierkant niets verandert aan de 'magische' eigenschappen van dit vierkant.
Kortom, wat jij zegt in jou comment lijkt zo veel op wat ik zei in de mijne, dat het bijna zeker zo is dat jou comment een kopie van de mijne is. En nee, dat meen ik niet, maar het is vergelijkbaar met de redenering die ik hier over de magische vierkanten hoor.
Het was aan mij niet meteen duidelijk dat de tweede operatie alle eigenschappen van het Franklin-zijn zou behouden, zoals bijvoorbeeld de magische som op de gebroken diagonalen. Het vereist ook best wel enige manipulatie met de gegevens om dit af te leiden.
Bovendien werken wij met wetenschap van achter af: we hebben twee vierkanten die louter verschillen in het wisselen van twee tweetallen rijen, dus we vragen ons af of dit altijd kan. Als ik de eisen van een Franklin-vierkant zie, schiet bij mij niet direct het idee in m'n hoofd dat tweetallen van rijen verwisselen misschien wel de eigenschappen behoudt.
Om toch nog een constructieve twist aan dit verhaal te geven, gooi ik de volgende vragen in de groep:
1. Hoeveel redundantie zit er in de eisen van Franklin magische vierkanten?
2. Wat voor transformaties zitten er zeker in de symmetriegroep van een Franklinvierkant?
dinsdag 10 april 2007 om 13:41
(#59) Hey Marco
ik denk dat je volkomen gelijk hebt, ik kan inderdaad veel figuren maken die allemaal 2056 uitkomen dankzij het feit dat elk vierkantje van 4 op 4 als som 514 heeft, maar nu ja, ik vind het gewoon tof om allerlei figuren te ontdekken die allemaal 2056 uitkomen alhoewel ik weet dat veel figuren uit andere tevoorschijn komen.
Heeft er ondertussen al iemand mijn vierkant gecontroleerd? Normaal zouden er geen fouten in mogen zitten, maar je weet maar nooit...
En aan DJ Bravey: nee ik heb geen copyright gebruikt =) maar het lijkt wel duidelijk aan deze site dat ik dat vierkant gemaakt heb zeker? Nu ja, van den Essen heeft ondertussen mijn vierkant ook, maar het is nu al weer even geleden dat ik nog reactie kreeg van hem... Het is natuurlijk ook wel paasweekend geweest hé.
Mvg. Jordy
woensdag 11 april 2007 om 19:50
Als je naar de eerste en de laatste rij kijkt in dit vierkant zie je steeds x en 145-x tegenover elkaar liggen waarbij x tussen 1 en 12 ligt. Aangezien je 1 tot en met 12 niet in 4 gelijke porties kunt verdelen(linksboven, rechtsboven, linksonder en rechtonder) is het onmogelijk om aan alle eisen van een franklinvierkant te voldoen.(1+2+..+12 = 6*(1+12) is niet deelbaar door 4). Als je naar het 8 bij 8 franklinvierkant kijkt is dat wel zo: 1+2+...+8 = 4*(1+8) is wel deelbaar door 4. Het is zelfs zo dat van elk vierkant met een zijde 8k+4 geen franklinvierkant gemaakt kan worden.
Dat de getallen op deze manier in het vierkant moeten staan komt door de andere eigenschappen; als je er zelf even mee bezig bent is alles erg logisch.
vrijdag 13 april 2007 om 15:13
Jippe, ik zou graag een bewijs willen zien van jouw bewering dat er geen 8k+4 (ihb 12) franklin vierkant mogelijk is.
Het is overigens heel goed mogelijk een franklin vierkant te hebben dat niet axiaal-symmetrisch is:
[51 60 3 12 19 28 35 44]
[13 2 61 50 45 34 29 18]
[52 59 4 11 20 27 36 43]
[10 5 58 53 42 37 26 21]
[54 57 6 9 22 25 38 41]
[ 8 7 56 55 40 39 24 23]
[49 62 1 14 17 30 33 46]
[15 0 63 48 47 32 31 16]
Maar ik ben er eigenlijk ook niet echt mee bezig dus misschien is het ook niet allemaal erg logisch :-)
P.S. oh en mocht je opvallen dat ik niet 1,2.. 64 gebruikte: tel bij elk getal 1 op.
zaterdag 14 april 2007 om 19:23
Laat ik dit voorbeeld gebruiken:
109 35 119 25 115 32 116 31 117 27 111 33
24 122 14 132 18 125 17 126 16 130 22 124
1 143 11 133 7 140 8 139 9 135 3 141
144 2 134 12 138 5 137 6 136 10 142 4
121 23 131 13 127 20 128 19 129 15 123 21
36 110 26 120 30 113 29 114 28 118 34 112
97 47 107 37 103 44 104 43 105 39 99 45
60 86 50 96 54 89 53 90 52 94 58 88
61 83 71 73 67 80 68 79 69 75 63 81
84 62 74 72 78 65 77 66 76 70 82 64
85 59 95 49 91 56 92 55 93 51 87 57
48 98 38 108 42 101 41 102 40 106 46 100
Dit ogenschijnlijke franklinkvierkant mist 1 eigenschap, dat de som van een willekeurige gebroken diagonaal niet de magische som oplevert. Echter bij de horizontale gebroken diagonalen zit maar een fout van 2(om en om 868 en 872). Dit komt omdat 1+11+7 niet gelijk is aan 8+9+3. Doordat het verschil 1 is en alle getallen zich tot elkaar verhouden (de som van 2 horizontaal naast elkaar liggen getallen is gelijk aan de som van de 2 er onder of boven, zelfde geldt voor verticaal maar dan de 2 links of rechts ervan)
wordt dat verdubbeld omdat 143+133+140 1 meer is dan 139+135+141. Als je er even mee bezig bent in Excel is het al snel duidelijker.
Als je dit probleem zou kunnen oplossen zou je een franklin vierkant kunnen maken van 12 bij 12, maar omdat de som van 12 willekeurige opeenvolgende getallen niet deelbaar is door 4 wil dat dus niet
zondag 15 april 2007 om 00:16
@jippe: Ik snap nu pas dat je niet de goede definitie hebt van een franklin vierkant. Het is inderdaad onmogelijk om 1 diagonaal goed te hebben en ook de gebogen gebroken diagonalen etc. bij deze zijde. Voor de correcte eisen zie mijn website:
http://www.puzzled.nl/franklin/
zondag 15 april 2007 om 01:07
Ik heb de goede definitie wel zeker, want ik had hem in eerste instantie al van jouw site gehaald, ik zeg dus ook dat dit geen franklin vierkant is...
Op je site en op vele anderen kon ik niet echt een reden vinden waarom het niet mogelijk was om zo'n vierkant te maken en wat me opviel staat in mijn vorige posts.
zondag 15 april 2007 om 15:59
Ik zie nu waar de miscommucatie op berust, waar ik zei gebroken diagonalen bedoelde ik gebogen diagonalen. De diagonalen van linksboven naar het midden naar rechtsboven etc.
maandag 16 april 2007 om 10:20
@Jippe: Ik heb je comments toch nog eens (beter) gelezen.
De drietallen die je aanwijst dienen idd gelijk zijn willen de gebogen diagonalen de goede som krijgen. Zie ook fig. 2 van
http://www.puzzled.nl/franklin/frank12.pdf
waar 't iets preciezer staat.
Ik begrijp dat je beweert dat dat niet kan als aan de andere eisen is voldaan (fig 1. van bovenstaande pdf) omdat 4 geen deler is van 12 opeenvolgende getallen!? Dat volg ik niet.
Ik neem aan dat je comment 63 als argument aanvoert. Maar ik zie niet in waarom bv. 1,2,..12 persé opgesplitst moet worden in 4 gelijke som delen over de vier "kwadranten" van het vierkant. Het 8x8 franklin-vierkant van comment 64 bevat bijvoorbeeld in het rechtsboven vierkant geen van de cijfers 1,2,...,8.
mmm ik zal er wanneer ik echt tijd heb eens naar kijken.
dinsdag 17 april 2007 om 13:43
@Christian: Dat klopt, het vierkant wat je gepost hebt in 64 is zeg maar een kwartslag gedraaid. In kolom 2 en 3 staan 0 en 7, 1 en 6, 2 en 5, 3 en 4 bij elkaar en zo ook de getallen 63-0 en 63-7 etc. Op dezelfde manier zijn de andere paren ook in het vierkant geplaats.
donderdag 19 april 2007 om 16:01
@Jippe: Ik begrijp dat je een verband denkt te zien in de plaatsing van complementaire getallen.
Als 1,2,..,N*N gebruikt in het vierkant dan zijn dan is het complement van van een getal x gelijk aan N*N-x.
Bij zijde N=12, zijn complementaire paren bijv. (1,144), (2,143) en (33,111).
Alle mogelijke Franklin vierkanten van zijde 8 zijn naar complementaire paren ingedeeld in in 8 typen/groepen door Miguel Amela zie
http://www.region.com.ar/amela/franklinsquares/
Let op hij laat echter de constante som voor de 2x2-blokken weg!
Maar wat is nu precies je redenering of bewering waaruit zou moeten volgen dat je bij zijde 12 je twaalf opeenvolgende getallen in 4 gelijke som delen moet splitsen (wat uiteraard onmogelijk is)?
maandag 23 april 2007 om 16:05
@Christian
Als 2 rijen elkaars complement zijn dan zitten er 6 getallen in tussen 12x+1 en 12(1+x) en 6 getallen tussen 145-(12x+1) en 145-(12(1+x)) waarbij x tussen 0 en 11 ligt. Doordat links en rechts van het midden en beide gekozen rijen dezelfde som op moet leveren moeten die 24 getallen waarvan er 12 complementaire paren zijn in 4 gelijke stukken worden gedeeld.
In het vierkant F2 van je gegeven link zijn wat getallen met elkaar verwisseld maar je kunt bij een 12 bij 12 vierkant bij elk getal 12x aftrekken zonder dat je de deelbaarheid door 12 veranderd. Zo heb ik ook dit vereenvoudige vierkant gemaakt:
1 11 11 1 7 8 8 7 9 3 3 9
12 2 2 12 6 5 5 6 4 10 10 4
1 11 11 1 7 8 8 7 9 3 3 9
12 2 2 12 6 5 5 6 4 10 10 4
1 11 11 1 7 8 8 7 9 3 3 9
12 2 2 12 6 5 5 6 4 10 10 4
1 11 11 1 7 8 8 7 9 3 3 9
12 2 2 12 6 5 5 6 4 10 10 4
1 11 11 1 7 8 8 7 9 3 3 9
12 2 2 12 6 5 5 6 4 10 10 4
1 11 11 1 7 8 8 7 9 3 3 9
12 2 2 12 6 5 5 6 4 10 10 4
Dit is hetzelfde vierkant als die van #65 maar dan zovaak mogelijk 12 er van af. Wellicht geeft dit meer inzicht.
maandag 30 april 2007 om 11:32
Hey Jordy,
W'l jen me da vierkant van 16*16 ook n'n keer doorsturen? 'k z'n er erg in g'intreseerd!
Greeeeetz Saskiaa xX
vrijdag 4 mei 2007 om 19:28
@Saskiaa
hey
twas lang geleden dat ik hier nog eens op deze site was, maar blijkbaar is er nog steeds interesse in mijn vierkant =). Het probleem is wel dat ik je e-mail niet heb hé. en als ik op je naam klik opent mijn computer niets. terwijl ik dacht dat er een website of zoiets ging verschijnen...
Mvg. Jordy
zaterdag 19 mei 2007 om 12:16
wtf is dit voor een site man .
mensen die van wiskunde houden wtf.
ga toch wat nuttigs doen zoals Guildwars Factions
zaterdag 19 mei 2007 om 12:24
@dooie eend: Als jij meent dat wiskunde niet nuttig zou zijn realiseer je je blijkbaar niet hoeveel wiskunde je zelf dagelijks gebruikt. Net als vele anderen heb je op de basisschool de getallen leren kennen en er mee leren rekenen, en waarschijnlijk heb je toen ook wel het een en ander geleerd over lengte-, oppervlakte- en inhoudsmaten. Als het goed is pas je die kennis nog regelmatig toe om bepaalde situaties uit het dagelijks leven op te kunnen lossen. Denk bijvoorbeeld aan het narekenen van je elektriciteitsrekening, of het berekenen hoeveel vierkante meter linoleum je eigenlijk nodig hebt voor het bedekken van een vloer. Als je hiermee bezig bent, ben je ook al met wiskunde bezig, en zelfs met zeer elementaire wiskunde. Je kunt wat dat betreft dus moelijk volhouden dat wiskunde niet nuttig zou zijn, integendeel zelfs.
zaterdag 2 juni 2007 om 01:48
Hallo. Toen ik vanmorgen wakker werd, was het eerste wat ik dacht het nieuws over het magische vierkant wat jullie voor elkaar gekregen hebben. Nu moet ik toegeven dat ik totaal niet weet hoe bijzonder dit is maar wat ik wel weet is dat ik wat met die gedachte moet.
Nu ik hier al die commentaren heb gelezen waar naar mijn mening nogal denigrerend over jullie prestatie word gedaan wil ik alleen maar tegen jullie zeggen.
Geweldig gedaan. Ik ben trots op jullie.
Mensen als jullie heeft de wereld nodig en ik hoop dan ook dat jullie een geweldige toekomst tegemoet gaan.
donderdag 7 juni 2007 om 13:18
Hey
tis een tijdje geleden maar hier ben ik nog eens. Heeft er iemand het tijdschrift natuur wetenschappen en techniek al gelezen van juni? Op pagina 11 staat daar zogezegd een magisch vierkant van Barbieri. Ik vind het echter schandalig! In het artikel staat dat de rijen kolommen en de beide diagonalen 2056 uitkomen als je echter die diagonalen controleert komen ze 1032 en 3080 uit en dat is zeker geen 2056! Ik vind het dan ook verbijsterend dat ze dit publiceren zonder te controleren of wat er staat wel juist is. Bijgevolg is dit vierkant niet zuiver magisch (per definitie zouden de diagonalen juist moeten zijn en dat zijn ze niet!) en ook niet pandiagonaal magisch! Ik begrijp dan ook niet goed waarom men beweert dat deze man die drie scholieren zou hebben evenaart, want dat heeft hij niet!
Ik ben benieuwd naar jullie reacties.
Jordy Vanpoucke
zondag 10 juni 2007 om 21:05
ey kben pas 13 best wel vet dat vierkant
zondag 10 juni 2007 om 21:06
die gast van 75 is een aap echt zo'n gamefreak
maandag 3 december 2007 om 14:03
Ondertussen ben ik erin geslaagd, te laat om te publiceren een megemagisch 16 bi 16 vierkant te maken.Alle diagonalen kloppen, het is helemaal Franklinmagisch, en te vergelijken met het 12 bij 12 vierkant. Er zijn bovendien vele extra kwart rijen en kolommen en halve rijen en kolommen te vinden ( vijf extra van beiden)
Marco Barbieri
maandag 3 december 2007 om 17:23
5x moet zijn 3x. Uit dit 16x16 vierkant zijn 3x3x3x2=54 verschillende vierkanten te maken met praktisch dezelfde eigenschappen. Ze verschillen alleen in het aantal mogelijke figuren die symmetrisch t.o.v. de middenverticaal zijn en bij op en neer bewegen dezelfde waarde behouden. Bij sommigen is dit aantal niet maximaal.
Kortom, het perfecte magische vierkant, waaruit gemakkelijk een perfect vierkant van 32x32 te maken is.
dinsdag 4 december 2007 om 16:59
Is er iemand die weet of er in de rij oneven getallen nooit vier niet-priemgetallen elkaar opvolgen, m.a.w. of er in elke deelverzameling van vier opeenvolgende oneven getallen ten minste 1 priemgetal te vinden is?
Dan is de stelling dat elk even getal te schrijven is als de som van twee priemgetallen gemakkelijk te bewijzen. Maar ja, hoe bewijs je wat ik vraag?
dinsdag 4 december 2007 om 17:07
@ Marco:
Er zijn willekeurig lange rijtjes niet-priemen. Neem een groot getal n en bekijk de rij n!+2, n!+3, n!+4, ..., n!+n. Het is duidelijk dat al deze n getallen niet priem zijn, want n!+k is deelbaar door k als k ≤ n is. (En je kunt dus ook willekeurig lange rijtjes opeenvolgende oneven niet-priemgetallen maken op deze manier door de even getallen er uit weg te laten.)
Voor een rijtje van lengte 4 is het kleinste voorbeeld: 115, 117, 119, 121 zijn allemaal niet priem.
dinsdag 4 december 2007 om 17:11
Volgens Jordy zijn er 32 gebogen diagonalen in een 16x16 vierkant. Ik dacht toch echt dat dat er 64 zijn, net als de gewone diagonalen en gbroken varianten.
donderdag 17 januari 2008 om 13:55
Ik vind deze wiskunde vierkant tog zo leuk. Op dit moment ben ik ook zo blij om een wiskundenurd te zijn! echt geweldig zeg!
donderdag 17 januari 2008 om 13:57
hahaha wat een zielig 'magisch vierkant' het lijkt helemaal nergens op!!!!! dit is echt een zieligge site en van die foto van jullie moest ik bijna kotsen.
woensdag 19 maart 2008 om 18:18
Is de foto ,of poster die op de achtergrond bij de foto waar jullie gezellig samen tegenover elkaar liggen ontleend aan de tekening van Escher met een figuur in een prentengallery die kijt naar een schilderij, of prent, waar hij weer zelf in voorkomt, waar hij weer kijkt naar een prent waar hij weer zelf in voor komt etc.? Escher wist zelf niet het midden in te vullen , maar in kete is het een oneundige lijst waarvan de zijden steeds kleiner worden en misschien is het ewl een leuke opgave om te bekijken of de som van een van de steeds kleiner wordende zijden convergeert.
Oh ja Jeanine, bedankt nog voor de tip over die priemgetallen. Ik ben nog steeds , of beter gezegd af en toe, aangezien nog veel andere dingen mij interesseren, het probleem dat elk even getal te schrijven is als de som van twee priemgetallen op te lossen. Er moet toch een methode zijn.
Hartelijke groetjes, Marco Barbieri
vrijdag 31 oktober 2008 om 19:48
12 247 1 254 8 251 13 242
213 42 224 35 217 38 212 47
188 71 177 78 184 75 189 66
101 154 112 147 105 150 100 159
204 55 193 62 200 59 205 50
21 234 32 227 25 230 20 239
124 135 113 142 120 139 125 130
165 90 176 83 169 86 164 95
92 167 81 174 88 171 93 162
133 122 144 115 137 118 132 127
236 23 225 30 232 27 237 18
53 202 64 195 57 198 52 207 156 103 145 110 152 107 157 98
69 186 80 179 73 182 68 191
44 215 33 222 40 219 45 210
245 10 256 3 249 6 244 15
Dit is de linkerkant van het perfecte 16x16 vierkant. Dan volgt nu de rechterhelft:
11 248 2 253 7 252 14 241
214 41 223 36 218 37 211 48
187 72 178 77 183 76 190 65
102 153 111 148 106 149 99 160
203 56 194 61 199 60 206 49
22 233 31 228 26 229 19 240
123 136 114 141 119 140 126 129
166 89 175 84 170 85 163 96
91 168 82 173 87 172 94 161
134 121 143 116 138 117 131 128
235 24 226 29 231 28 238 17
54 201 63 196 58 197 51 208
155 104 146 109 151 108 158 97
70 185 79 180 74 181 67 192
43 216 34 221 39 220 46 209
246 9 255 4 250 5 243 16
Ok t.o.v. de verticale as is een symmetrie aanwezig die echter niet zo maximaal is als t.o.v de horizontale as, maar meer is niet mogelijk. Er is aan alle eisen van een Franklin vierkant voldaan en ook de gewone diagonalen en hun gebroken varianten leveren het magische getal (2056). Bovendien zijn er extra halve rijen en kwart rijen die de helft of een kwart van het magische getal opleveren. Vanuit dit vierkant zijn equivalente vierkanten te construeren, zodat er meerdere vierkanten met dit maximaal aantal mogelijkheden
zondag 2 november 2008 om 16:31
De getallen 156 103 145 110 152 107 147 98 horen boven de derde rij van onderen van de linkerkant van het vierkant. Uit dit vierkant zijn natuurlijk ook equivalente vierkanten van 32x32, 64x64, etc. te construeren.
vrijdag 27 maart 2009 om 19:06
Weten jullie of er een bewijs is voor de stelling dat elf even getal geschreven kan worden als de som van twee priemgetallen?
zaterdag 28 maart 2009 om 01:26
@Marco. Elk even getal te schrijven als ... is het vermoeden van Goldbach, een beroemd onopgelost probleem in de wiskunde. Als daar een bewijs voor gevonden wordt zetten de meisjes het op de voorpagina. Kortom, zo'n bewijs is er (nog) niet. Met de computer is de bewering al gecontroleerd voor bijzonder grote getallen. Dat telt niet als bewijs, maar geeft weinig hoop dat iemand een voorbeeld weet te vinden dat de 'stelling' tegenspreekt.
zaterdag 28 maart 2009 om 01:36
78 niet meegerekend natuurlijk
zaterdag 28 maart 2009 om 11:50
@Vincent: 78 is te schrijven als 7+71, aangezien 7 en 71 allebei priemgetallen zijn.
dinsdag 31 maart 2009 om 13:06
Dit is echt een kut site zeg! Ken je mij nog van donderdag 17 januari? Wat was dat een positieve dag. Toen vond ik het wel leuk. Na wat research wist ik dat ik hier echt van moest kotsen.
dinsdag 31 maart 2009 om 13:07
Deze site is echt de beste site die er is! IK kijk er elke dag op en probeer dan zelf ook zo'n vierkant te maken. Jullie zijn zo inspirerend. Ik zou graag met jullie uitgaan! jullie zijn zo intelligenttt. Ik was in het verleden wat negatief maar nu ben ik tot inkeer gekomen!
vrijdag 27 mei 2011 om 15:08
KAAS = BAAS