Internetbureau Rotterdam 
Dit bericht is geplaatst op donderdag 3 mei 2007 om 09:30 in categorieën Algemeen. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Het vermoeden van Goldbach (4)
In Algemeen, door wiskundemeisjes
Een jaar geleden schreven we hier, hier en hier over het vermoeden van Goldbach. Dat vermoeden zegt: ieder even getal groter dan twee is te schrijven als de som van twee priemgetallen.
Dit klinkt niet zo ingewikkeld, maar het blijkt toch heel moeilijk te zijn: tot nu toe is niemand er in geslaagd om het daadwerkelijk te bewijzen. Wel zijn al heel veel even getallen gecontroleerd. Vorige week hoorden we het nieuws dat inmiddels alle even getallen van 4 tot 1018 geverifieerd zijn: die zijn inderdaad allemaal te schrijven als som van twee priemgetallen. Dit levert natuurlijk helemaal geen garantie op dat het ook geldt voor alle getallen groter dan 1018, hoe indrukwekkend dat getal er ook uitziet.
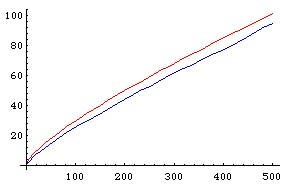
Er bestaat een goed voorbeeld van een probleem dat ook over priemgetallen gaat waarbij de tabellen enigszins misleidend waren, ook al gingen ze tot heel grote getallen. Gauss vroeg zich af: stel dat je een groot getal N hebt, hoeveel priemgetallen bestaan er die kleiner zijn dan N? Hij gaf een schatting voor dit aantal in termen van N. Gauss dacht dat zijn schatting steeds beter klopt als N groter wordt, en dat is inderdaad het geval. Maar hij dacht ook dat zijn schatting altijd te ruim zou blijven. In de tabellen zag het er inderdaad zo uit, en zelfs tot heel grote getallen is dat zo. Maar in 1912 bewees Littlewood dat Gauss' schatting soms toch te laag uitvalt. De eerste keer dat dat gebeurt is echter pas bij een getal dat groter is dan het aantal atomen in het waarneembare heelal! Lees meer hierover in dit artikel uit Plus magazine.
Laten we dus vooral hopen op een echt bewijs van het vermoeden van Goldbach, want met controleren alleen komen we er niet. Tenzij we op een dag ontdekken dat het vermoeden niet waar is door een tegenvoorbeeld te vinden!
Lees verder over het vermoeden van Goldbach en een vermeend bewijs op Kennislink.
(Jeanine)
