Dit bericht is geplaatst op vrijdag 15 juni 2007 om 15:33 in categorieën Muggenziften. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Een formule! Een formule?
In Muggenziften, door wiskundemeisjes

Als lijstjesgek ben ik dol op de Internet Movie Database (IMDb voor vrienden). Ze houden ook een lijst bij van de top 250 van de beste films, die door stemmen van gebruikers wordt bepaald. Laatst viel me op dat onderaan die pagina een formule staat. Ik vond het heel goed dat ze lieten zien hoe de lijst werd samengesteld en wilde hier al een lovend stukje schrijven over de IMDb. Tot ik eens beter naar de formule keek. Dit is hem:
beoordeling = (v ÷ (v+m)) × R + (m ÷ (v+m)) × C,
waarbij
R = het gemiddelde cijfer dat de film krijgt,
v = het aantal stemmen voor de film,
m = het minimale aantal stemmen dat nodig is om in de lijst te komen (op dit moment 1300),
C = het gemiddelde cijfer over alle films genomen (op dit moment een 6.7).
Op de IMDb zeggen ze dat dit een true Bayesian estimate is. Ik vroeg aan een voorbij rennende hoogleraar in de statistiek of dat klopte. Hij antwoordde: "Onzin! Dit heeft niets met Bayes te maken, dit is gewoon een gewogen gemiddelde met een paar constantes erin."
Mij verbaast het vooral dat de drempelwaarde m op deze manier gebruikt wordt. Je zou willen dat voor films waarbij het aantal stemmen (v) lager is dan m, er iets geks uit de formule komt (iets negatiefs of heel kleins). Maar dat is helemaal niet het geval, zoals dit eenvoudige plaatje (waarbij het aantal stemmen loopt van 1000 tot 1500) laat zien.
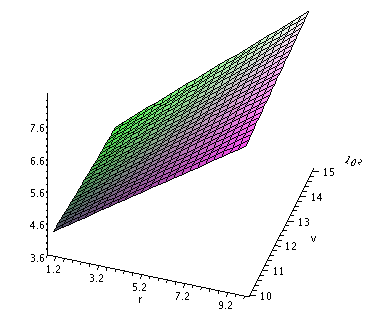
Zouden ze niet liever v-m gebruiken in plaats van v+m (hoewel dat in de noemer zeker geen goed idee is)? Of zie ik iets over het hoofd?
(Ionica)
 Internetbureau Rotterdam
Internetbureau Rotterdam 
