Dit bericht is geplaatst op donderdag 16 augustus 2007 om 09:00 in categorieën Algemeen, Puzzels. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Wiskundemeisjes op kamp (4)
In Algemeen,Puzzels, door wiskundemeisjes
Probleem 4: Cake snijden
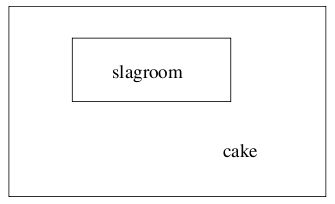
Op een rechthoekige cake is slagroom gespoten, ook in een rechthoekige vorm (zoals op het plaatje). Je wil de cake in twee stukken delen, maar natuurlijk wel zó dat je allebei evenveel cake krijgt en evenveel slagroom. Je mag één keer snijden, in een rechte lijn. Hoe doe je dat?
(Jeanine)
 Internetbureau Rotterdam
Internetbureau Rotterdam 
