Internetbureau Rotterdam 
Dit bericht is geplaatst op dinsdag 23 oktober 2007 om 11:20 in categorieën Trivia. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Wat is de mooiste rechthoek?
In Trivia, door Ionica
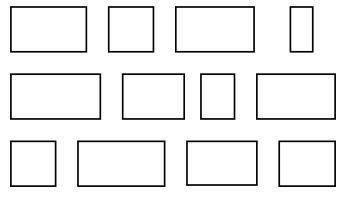
Wat vinden jullie de mooiste rechthoek? Voor het gemak heb ik de rechthoeken hieronder genummerd.
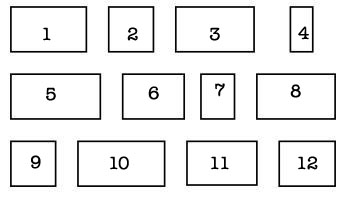
[poll=6]
Zoals jullie misschien al raadden: één van deze rechthoeken heeft verhoudingen die dicht bij de gulden snede liggen. Ik vroeg me af of mensen die nou echt mooier vinden. Later deze week zal ik vertellen welke de gulden rechthoek is!
dinsdag 23 oktober 2007 om 12:23
Ik hou meer van cirkels.
dinsdag 23 oktober 2007 om 14:21
Wat grappig, ik heb op 8 gestemd en die blijkt de meeste stemmen te hebben!
Ik ben benieuwd welke de gulden-snede-verhoudingen heeft!
dinsdag 23 oktober 2007 om 14:33
Ik vind nummer 4 ook wel mooi; die lijkt het meest op een Kapla-plankje!
dinsdag 23 oktober 2007 om 15:28
Heeft de schoonheid er ook niet mee te maken of de rechthoek 'staat' of 'ligt'?
dinsdag 23 oktober 2007 om 17:18
Ik vind 11 het mooiste, edoch nummer 6 vind ik gevoelsmatig meer bij 'den vergulden snede' passen...
dinsdag 23 oktober 2007 om 17:19
Ik heb op een rechthoek gestemd, maar er zitten andere in de verzameling die zo op het oog dezelfde afmetingen hebben. Voor mij lijkt het ook uit te maken wat de positie van de rechthoek binnen de verzameling is.
dinsdag 23 oktober 2007 om 18:05
Wat mij betreft: hoe symmetrischer, hoe mooier.
dinsdag 23 oktober 2007 om 18:15
3 en 8 lijken wel hetzelfde, maar dat kan inderdaad ook optisch bedrog zijn door hun plaats in de verzameling.
En ik vond het ook lastig om oprecht te kiezen voor de mooiste, zonder stiekum te zoeken naar de rechthoek die me het dichtst bij 1:1.618 zat (de drang om het antwoord 'goed' te hebben).
dinsdag 23 oktober 2007 om 18:56
En wat het mooiste van allemaal is... De 5 populairste hun verhouding lengte/breedte liggen het dichtst bij de gulden verhouding...
dinsdag 23 oktober 2007 om 19:01
Mmm...ik had dat van de gulden snede er misschien niet bij moeten zetten, want volgens mij proberen nu meer mensen het "goede" antwoord te kiezen. Er zijn trouwens heel veel studies gedaan naar dit soort keuzes, met nogal verschillende uitkomsten. Ik kan die publicaties echter niet gratis opvragen (wiskunde heeft geen abonnement op psychologietijdschriften). Als iemand wel toegang heeft tot dat soort dingen, wil die dan even mailen? Dan kan ik meer lezen dan de abstracts!
dinsdag 23 oktober 2007 om 20:23
En hier zie je dat het jammer is dat er zo'n strikte grens is tussen de studierichtingen.
En waar wiskunde en psychologie in elkaar overlopen... en kunst, bouwkunde?
Als iemand nog iets heeft voor mijn 'niet commerciele winkel'(NL site), over wiskunde of psychologie, laat het mij weten!
@Ionica, ik heb een link naar een site met allemaal psychobiologen en psychofysiologen in Massachussets op mijn site in de marge. Misschien iets voor jou?
http://www.schmiodile.blogspot.com (VS site)
Is het nieuw dat je geen toegang hebt tot Psychologische tijdschriften als wiskundige?
dinsdag 23 oktober 2007 om 21:10
Ha Odile, op zich heb ik wel toegang tot tijdschriften van andere vakgebieden, ik kan naar de bibliotheek van andere faculteiten om ze op te zoeken. Ik kan ze alleen niet online lezen...
dinsdag 23 oktober 2007 om 21:31
De Leidse universiteit geeft toegang vanaf je werkcomputer tot alle tijdschriften van grote uitgevers als Elsevier, Springer, en nog zo wat. Ongeacht onderwerp. Ik weet niet welke tijdschriften je wilt lezen Ionica?
dinsdag 23 oktober 2007 om 21:44
Haha, lol!
Een van de Wiskundemeisjes is Ionica!
Dat had ik moeten weten!
dinsdag 23 oktober 2007 om 22:03
Eigenlijk zou dit onderzoek onder niet-wiskundigen moeten gebeuren, want ik vond het moeilijk om niet aan de gulden snede te denken. En als je dat probeert, dan ben je ook weer bevooroordeeld. Lastig. Verder ben ik benieuwd of de oriëntatie van de rechthoek uitmaakt: of de hoogte groter is dan de breedte of omgekeerd. Volgens tellen beide type rechthoeken die de gulden snede benaderen.
dinsdag 23 oktober 2007 om 22:09
Ik heb 8 gestemd, hoewel 1 en 3 me nagenoeg hetzelfde lijken. (Als ze niet al hetzelfde zijn.)
Waarom? Omdat ze lang genoeg zijn om een mooie rechthoek uit te beelden (Vierkanten een rechthoek noemen is allemaal wel leuk, maar daar hebben we het woord vierkant dus al voor, dus dat doe je maar leuk thuis met vrienden.) en kort genoeg om niet "eng" langerekt over te komen. Wat mij betreft benaderen 1, 3 en 8, gevolgd door 11 het meest het archetype "rechthoek" zoals ik dat voor me zie.
dinsdag 23 oktober 2007 om 22:11
Klaas-Jan: stiekum is het allemaal nog erger want door ze bij elkaar te zetten beïnvloed je ook nog de perceptie en met de nummers er in helemaal!
dinsdag 23 oktober 2007 om 22:15
*Zwaait naar Ed*
HJ: Ik wilde het artikel "The Golden Section Hypothesis" van C. Plug lezen, uit The American Journal of Psychology, Vol. 93, No. 3 (Sep., 1980), pp. 467-487.
Zie: http://links.jstor.org/sici?sici=0002-9556(198009)93%3A3%3C467%3ATGSH%3E2.0.CO%3B2-M
Ik kreeg een melding dat mijn instituut geen directe toegang heeft tot dit tijdschrift. Ik heb er verder niet superveel moeite voor gedaan. Ik heb het niet nodig voor mijn onderzoek, dit is maar een hobby...
Hoewel, vandaag was ik een grens aan het berekenen en na twee kantjes rekenwerk kwam ik uit op de gulden snede. Het was een leuke dag!
dinsdag 23 oktober 2007 om 23:15
Helaas, daar zijn we inderdaad niet op geabonneerd. Wel vond ik een artikel met dezelfde titel, British Journal of Psychology, 1976. Vraag proefpersonen om een aantal bekenden in te delen in tegengestelde categorieen (vrijgevig-gierig, aktief-passief) en de verdeling valt voor 62% in de positieve categorie. De gulden snede onder maar liefst 30 undergraduate vrijwilligers. (De kaartjes werden trouwens tussendoor goed geschud, dus dat zit wel snor. Grijns.)
woensdag 24 oktober 2007 om 13:30
Bij Natuurkunde op de middelbare school moesten we dit ook eens doen. Ik vond rechthoek X het mooiste. Vertelde de leraar me bloedserieus dat ik het fout had.
woensdag 24 oktober 2007 om 16:49
Ik ga de enquête uitvoeren bij m'n leerlingen van 14 jaar, benieuwd of ze het juist hebben.
woensdag 24 oktober 2007 om 16:55
Maar Kristof, er is toch geen goed of fout?
Enne..Patrick en Niels bedankt voor het opsturen van het artikel dat ik zocht!
woensdag 24 oktober 2007 om 21:15
Hoi Ionica,
leuk onderzoek, er zijn theorieen in omloop dat de gulden snede met terugwerkende kracht in de schoonheidsperceptie is ingelezen, dat het ideaal als puike verhouding eigenlijk pas rond de rennaisance werd 'ontdekt' en daarna werden er in oude+nieuwe tijden bewijzen bij gezocht.
Een prima boek dat op die kwestie ingaat is:
de ontstelling van pythagoras - A van der Schoot
Succes!
vrijdag 26 oktober 2007 om 10:22
ha ha, ik zie het nu pas, maar nummer 7 is natuurlijk de gulden snede! iedereen kijkt eroverheem omdat de meeste anderen liggen en 7 wat klein is, maar qua verhouding lijkt hij toch het meest op een a4tje!
vrijdag 26 oktober 2007 om 12:56
Hoe kan het toch zijn dat vierkanten 2 en 9 zo laag staan in de verhouding? Hoe gaaf is het dat voor de assen a en b geldt dat a=b !? Misschien dat het te maken heeft met mijn natuurkundeachtergrond, maar dit soort randgevallen zijn mijn favoriet. Overigens doen de "kleine" rechthoeken 4 en 7 het ook heel slecht.
vrijdag 26 oktober 2007 om 12:58
Overigens is een A4'tje niet gevormd naar de gulden snede. Een A4'tje heeft heeft verhouding 1:2^½ oftewel 1:1,414, de gulden snede is 1:½(5^½+1) oftewel 1:1,618.
vrijdag 26 oktober 2007 om 13:11
Die 'juist' was ironisch bedoeld Ionica.
vrijdag 26 oktober 2007 om 18:09
Als je iemand vraagt om een rechthoek te tekenen zal hij niet proberen een "zo mooi mogelijke" rechthoek te tekenen, maar een "zo willekeurig mogelijke rechthoek". Rechthoek ABCD zal met AB horizontaal getekend worden omdat dat de minste papier verspilling geeft, als er ook nog tekst bij moet. De verhouding AB/BC zal ergens tussen 1 en 2 liggen, AB/BC=1 en AB/CD>2 zijn te speciaal. Dat de meest gekozen verhouding in de buurt van 1,6 ligt komt denk ik eerder door het feit dat dit een "willekeurige" verhouding is dan een het "mooie" verhouding is.
zaterdag 27 oktober 2007 om 12:46
Ik heb eigenlijk geen voorkeur, maar ik weet dat nummertje 8 de gulden snede vertegenwoordigt of althans zeer dicht benadert. Vandaar...
zaterdag 27 oktober 2007 om 19:28
Ik heb ooit een praatje van twee wiskundeprofessoren bijgewoond over de gulden snede. Volgens hun is het gehyped. De manier waarop het in Griekse tempels terug komt slaat nergens op: daarbij werden willekeurige dingen gemeten als de afstand van de linkerkant van de tempel tot de linkerkant van de meest rechter pilaar. Verder was er een symfonie van Bach waarin het voor zou komen; ze legden uit hoe dat werkt en als huiswerkopdracht moesten we onze eigen naam uit die symofonie halen :)
zondag 28 oktober 2007 om 17:27
De gulden snede doet me nog altijd aan de film PI denken.
zondag 28 oktober 2007 om 19:38
Zouden de cijfers zelf de keuze kunnen beïnvloeden? Ik was bij het kijken naar de rechthoeken mét cijfers geneigd om rechthoek nummer 8 te kiezen. Kijkend naar de rechthoeken zonder cijfer was ik geneigd om 11 te kiezen.
dinsdag 30 oktober 2007 om 15:20
Ik denk dat er een sterke voorkeur bestaat voor "liggende" rechthoeken ten opzichte van "staande"rechthoeken. Zeker omdat hier het grootste deel ligt (lange zijde onder). Ook speelt waarschijnlijk grootte een rol. Niet alle rechthoeken zijn even groot. Een kleine zal denk ik minder snel gekozen worden.
Oplossing 'probleem' 1: Laat kiezen tussen zowel liggende als staande rechthoeken. Bij elke liggende rechthoek moet ook een gelijke staande rechthoek zijn. Zo kan je zien of er voorkeur is voor liggend of staand bestaat.
Oplossing 'probleem' 2: Maak alle rechthoeken gelijk van oppervlakte of omtrek (ik weet niet wat beter werkt, wat op zich ook wel interessant is om uit te zoeken, wat het meest de grootte-ervaring bepaalt).
dinsdag 30 oktober 2007 om 15:23
[...] Vorige week vroeg ik jullie: wat is de mooiste rechthoek? [...]
woensdag 14 mei 2008 om 19:30
welke heeft nou de gulden snede?
woensdag 14 mei 2008 om 19:31
laat maar, ik moet beter lezen;)
woensdag 22 oktober 2008 om 22:49
11
woensdag 22 april 2009 om 19:27
k vindt het 6de het mooiste.
dat lijkt meer op een vierhoek maar het is geen vierhoek ^__^
donderdag 23 april 2009 om 07:55
vierhoek? je bedoelt vierkant denk ik
een vierhoek is het wel degelijk
woensdag 11 november 2009 om 15:42
echt vet cool en gaaf dit kan ik gebruiken voor wiskunde en voor mijn werkstuk!
woensdag 11 november 2009 om 15:44
sorry ik bedoelde geen tsil maar tsjille ik moest effe aan het tsjilautomaat denke want die heeft het ook altijd over tsjil.
een dikke zoen,
elise
vrijdag 13 november 2009 om 17:06
heuj mensen,
hier weer wat van mij
ik vind dit zo'n vet coole website.
egt helemaal te gek.
mijn broertje timco vind het ook zo gaaf
zondag 29 september 2013 om 17:28
[…] Wiskundemeisjes » Wat is de mooiste rechthoek? […]
donderdag 24 oktober 2013 om 21:45
[…] Daems schreef aan een gynaecoloog die de gulden snede meende te signaleren in baarmoeders. Of test zelf of je een gulden-snede-rechthoek mooier vindt dan andere rechthoeken (of kijk hoe anderen […]