Dit bericht is geplaatst op vrijdag 4 januari 2008 om 15:00 in categorieën Puzzels. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Tetraëders in een kubus
In Puzzels, door Jeanine
Jan van de Craats mailde ons een interessante opgave die hij heel lang geleden verzon voor de Pythagoras-olympiade.
Hoeveel tetraeders (regelmatige viervlakken) met ribbenlengte 1 passen er in een kubus met ribbenlengte 1?
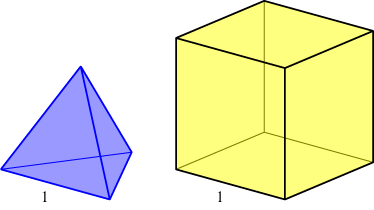
Wie weet de oplossing en vooral: wie kan bewijzen dat zijn oplossing klopt?
 Internetbureau Rotterdam
Internetbureau Rotterdam 
