Dit bericht is geplaatst op woensdag 9 januari 2008 om 23:41 in categorieën Puzzels. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Tetraëders in een kubus (2)
In Puzzels, door Jeanine
Ja ja, George heeft drie tetraëders met ribbenlengte 1 in een kubus met ribbenlengte 1 gepast! (Als je niet weet waarom dat bijzonder is, lees dan deze post even na, en vooral ook de reacties.)
Jan van de Craats mailde ons al een mooi plaatje met de gevonden oplossing:
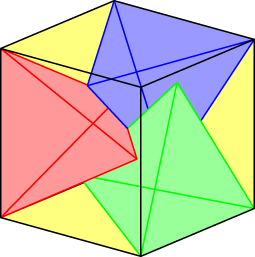
Maar de vraag blijft staan: kan iemand bewijzen dat er geen vier tetraëders met ribbe 1 in een kubus met ribbe 1 passen?
Toevoeging 14 januari: Nico Bakker stuurde ons dit filmpje, om een beter ruimtelijk idee te krijgen.
 Internetbureau Rotterdam
Internetbureau Rotterdam 
