Dit bericht is geplaatst op woensdag 27 februari 2008 om 08:16 in categorieën Kunst. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Origami
In Kunst, door Ionica
Vroeger vermaakte ik me uren met het vouwen van bloemen, doosjes en vooral veel kraanvogels. Ik ben daar allang meegestopt, maar toen ik het werk van Robert J. Lang zag, had ik zin om mijn vouwbeen weer op te pakken.

Op zijn prachtige website LangOrigami vind je allerlei vouwkunstwerken, maar ook uitleg over de origami axioma's:
- Door twee punten p1 en p2 gaat er precies één vouw.
- Voor twee punten p1 en p2, is er precies één vouw die p1 op p2 brengt.
- Voor twee lijnen l1 and l2, bestaat er een vouw die l1 op l2 brengt.
- Voor een punt p1en een lijn l1, is er precies één vouw loodrecht op l1 die door p1 gaat.
- Voor twee punten p1 en p2 en een lijn l1, bestaat er een vouw die p1 op l1 brengt en door p2 gaat.
- Voor twee punten p1 en p2 en twee lijnen l1 en l2, bestaat er een vouw die p1 op l1 en p2 op l2 brengt.
- Voor een punt p en twee lijnen l1 en l2, bestaat er een vouw loodrecht op l2 die p op l1 brengt.
De zeven axioma's geven alle mogelijke manieren om een vouw te creëren tussen mogelijke combinaties van punten en lijnen. Alles speelt zich natuurlijk af op een plat blaadje papier. De eerste zes axioma's werden in 1992 bedacht door Humiaki Huzita, Koshiro Hatori ontdekte het zevende axioma. Koshiro heeft zelf ook een mooie site over origami.
De grote vraag is nu wat je met deze vouwen wel en niet kunt construeren. Zoals jullie hopelijk wel weten, is het met de klassieke hulpmiddelen passer en latje onmogelijk om een willekeurige hoek in drie gelijke stukken te verdelen. Met origami kan dat wel!
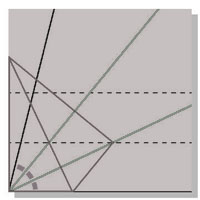
Lang beschrijft deze en allerlei andere constructies in Origami and Geometric Constructions (pdf). Hij schreef ook een hele rits boeken over origami, ook die zijn te vinden op zijn website. Bedankt voor deze tip Nico!
 Internetbureau Rotterdam
Internetbureau Rotterdam 
