Internetbureau Rotterdam 
Dit bericht is geplaatst op zaterdag 15 maart 2008 om 15:47 in categorieën Trivia. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
De stelling van Pythagoras
In Trivia, door Ionica
Iedereen (en ik bedoel ook echt iedereen) kent de stelling van Pythagoras: a2 + b2 = c2. Maar waar stonden die a, b en c ook al weer voor? En hoe kon je die stelling nou bewijzen? Ik leerde op school dat de stelling van Pythagoras geldt voor rechthoekige driehoeken en dat de stelling zegt dat de som van de kwadraten van de rechthoekszijden precies het kwadraat van de schuine zijde is.
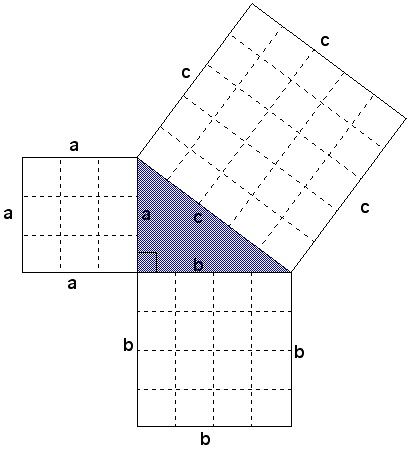
Er bestaan veel (en ik bedoel ook echt veel) bewijzen van de stelling van Pythagoras. Op Cut The Knot staan er bijvoorbeeld zevenenzeventig. Zelf vond ik dit plaatje altijd een erg mooi bewijs geven.
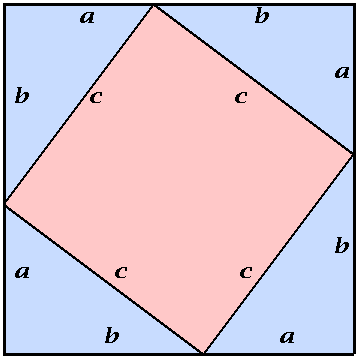
De oppervlakte van het grote vierkant is (a+b)2 = a2 + 2ab + b2. Maar je kunt de oppervlakte van het grote vierkant ook schrijven als de som van het kleine vierkant en vier driehoeken: c2 + 4 x 1/2 x ab = c2+2ab. En hieruit volgt dat a2+b2=c2. Maar snap je na dit bewijs nu ook echt wáárom die relatie geldt? Ik eigenlijk niet.
Gelukkig is er BetterExplained, een site vol met betere verklaringen (en dan bedoel ik ook echt beter). In Surprising Uses of the Pythagorean Theorem geeft Khalid Azad een heldere uitleg. Elke rechthoekige driehoek kan in twee kleinere rechthoekige driehoeken verdeeld worden (in het plaatje is gekozen voor a = 3, b = 4 en c = 5, maar het geldt natuurlijk altijd).
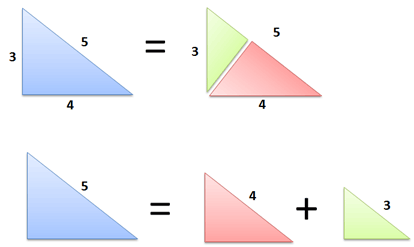
Lees de rest zelf op BetterExplained en ontdek hoe de stelling van Pythagoras ook werkt voor de grootte van pizza's of de tijd die nodig is om data te sorteren. Ik vond dit een tof voorbeeld:
Some programs with n inputs take n2 time to run (bubble sort, for example). In terms of processing time:
50 inputs = 40 inputs + 30 inputs
Pretty interesting. 70 elements spread among two groups can be sorted as fast as 50 items in one group. (Yeah, there may be constant overhead/start up time, just work with me here).
