Dit bericht is geplaatst op vrijdag 3 oktober 2008 om 11:48 in categorieën Leestip, Puzzels. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Een gemene gastheer
In Leestip,Puzzels, door Ionica
Op een conferentiediner moeten 48 mannelijke wiskundigen -geen van allen op de hoogte van tafel-etiquette- een grote, ronde tafel delen. De tafel is al gedekt en tussen elke twee borden ligt een servet. De gastheer plaatst de wiskundigen één voor één. Zodra een wiskundige gaat zitten, pakt hij een servet links of rechts van zijn bord. Als er aan elke kant nog een servet ligt, dan kiest hij er willekeurig één van de twee. De gastheer ziet niet welke servet de wiskundige pakt. Hoe moet de gastheer de wiskundigen neerzetten om het verwachte aantal wiskundigen zonder servet zo groot mogelijk te maken?
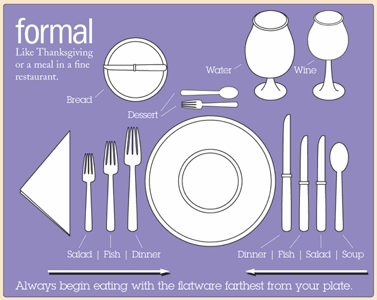
Het meest voor de hand liggende antwoord is niet het juiste! Deze leuke puzzel komt wederom van Peter Winkler. In zijn warm aanbevolen boek Mathematical Puzzles: A Connoisseur's Collection vertelt Winkler de oorsprong van deze puzzel.
This problem can be traced to a particular event. Princeton mathematician John H. Conway came to Bell Labs on March 30, 2001 to give a “General Research Colloquium.” At lunchtime, [Winkler] found himself sitting between Conway and computer scientist Rob Pike (now of Google), and the napkins and coffee cups were as described in the puzzle. Conway asked how many diners would be without napkins if they were seated in random order, and Pike said: “Here’s an easier question—what’s the worst order?”
De vraag van Conway is trouwens echt een stuk moeilijker!
 Internetbureau Rotterdam
Internetbureau Rotterdam 
