Dit bericht is geplaatst op woensdag 29 oktober 2008 om 09:25 in categorieën Nieuws. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Optimale Golomb-liniaal gevonden
In Nieuws, door Ionica
Steven mailde ons het heuglijke nieuws dat er een nieuwe optimale Golomb-liniaal is gevonden. ``Wat voor liniaal?'', hoor ik jullie vragen. Een Golomb-liniaal is een reeks positieve gehele getallen waarbij geen twee getallen uit deze reeks hetzelfde verschil hebben. Een voorbeeldje maakt het volgens mij veel duidelijker dan woorden.
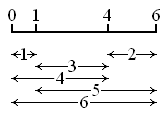
De reeks 0,1,4,6 vormt een Golomb-liniaal: elke twee getallen uit de reeks hebben een ander verschil.
Golomb-linialen kunnen verschillende eigenschappen hebben. Een perfecte liniaal bevat alle verschillen tussen 1 en zijn eigen lengte. Een optimale liniaal is de kortste liniaal met n getallen (waarbij kortste betekent dat het laatste getal uit de reeks zo klein mogelijk is). Het voorbeeld hierboven is zowel optimaal als perfect.
Het zoeken van optimale linialen is niet eenvoudig, sterker nog, er wordt vermoed dat dit een NP-volledig probleem is. Distributed.net maakte zaterdag bekend dat ze een optimale Golomb-liniaal met 25 getallen hebben gevonden. Hier is hij:
0 12 29 39 72 91 146 157 160 161 166 191 207 214 258 290 316 354 372 394 396 431 459 467 480.
Het duurde jaren rekenen met duizenden computers om te bewijzen dat deze Golomb-liniaal inderdaad de kortste is voor 25 getallen. De reeks zelf was overigens al in 1984 gevonden [1]. Op naar een liniaal met 26 getallen!
Het zoeken naar grote perfecte Golomb-linialen is trouwens nóg moeilijker. Vooral omdat bewezen is dat ze niet kunnen bestaan voor meer dan vijf getallen.
[1] M. D. Atkinson and A. Hassenklover, "Sets of Integers with Distinct Differences", School of Computer Science, Carlton University, Ottawa Ontario, Canada, Report SCS-TR-63, August 1984.
p.s. Vinden jullie ook niet dat zo'n voetnoot heel wetenschappelijk staat?
 Internetbureau Rotterdam
Internetbureau Rotterdam 
