Dit bericht is geplaatst op maandag 8 juni 2009 om 10:46 in categorieën Column. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Priemgetallen
In Column, door Jeanine
Deze column verscheen in de Volkskrant van 6 juni 2009.
Heeft u ook pas het boek "De eenzaamheid van de priemgetallen" van de Italiaanse debutant Paolo Giordano gelezen? Een boek met zo'n titel kon ik natuurlijk niet laten liggen. En hoewel ik het zeker goed geschreven vond, had ik na een tijdje wel genoeg van de problematische karakters. Nu wat aandacht voor de priemgetallen zelf dus, want die zijn ook heel interessant.

Een priemgetal is een getal dat geen andere delers heeft dan 1 en zichzelf. Per afspraak is het getal 1 geen priemgetal. De eerste priemgetallen zijn dus 2, 3, 5, 7, 11, 13, 17, 19. En zijn die priemgetallen echt zo eenzaam? Er bestaan oneindig veel priemgetallen, dus in die zin niet. Maar ze staan haast nooit naast elkaar in de rij van gehele getallen: 2 en 3 staan naast elkaar en zijn allebei priem, maar daarna schelen priemgetallen altijd minstens twee (want als twee getallen maar één schelen, is altijd één van de twee deelbaar door 2). En naarmate de getallen groter worden, worden de priemgetallen steeds zeldzamer: in de buurt van het getal 10.000 is ongeveer een op de negen getallen priem, en rond de 1.000.000.000 een op de 21.
Ook in de natuur komen priemgetallen voor. Een bekend voorbeeld is de levenscyclus van een bepaald insect, de cicade. Cicaden zijn een beetje rare beestjes: afhankelijk van de soort leven ze eerst dertien of zeventien jaar onder de grond, waar ze leven van sappen uit boomwortels, en daarna komen ze met z'n allen tegelijk naar boven om zich voort te planten. Binnen een maand gaan ze allemaal dood. Maar de larven laten zich weer uit de boomtakken naar beneden vallen, en kruipen dan weer voor dertien of zeventien jaar de grond in, enzovoort.
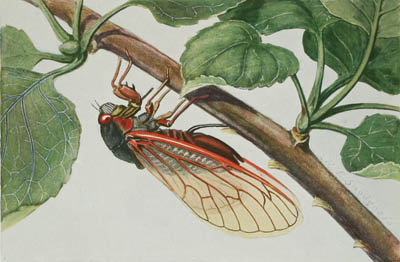
Wetenschappers vragen zich natuurlijk af: is het toeval dat de lengtes van deze cycli priemgetallen zijn, of zit daar een evolutionair voordeel aan vast? Bewijzen kun je het moeilijk, maar de hypothese is geopperd dat een priemgetal als cyclus handig is om natuurlijke vijanden te ontlopen. Als je vijand er elk jaar is, maakt het niet uit wanneer je als cicade bovenkomt. Maar mocht een natuurlijke vijand ook periodiek verschijnen, of met een bepaalde periode steeds meer of minder talrijk zijn, dan wil je als cicade liever niet bovenkomen op het moment dat het aantal vijanden ook piekt. Als je als cicade een twaalfjarige cyclus zou hebben, dan zou je vijanden die er eens per 1, 2, 3, 4, 6 of 12 jaar zijn elke keer als je bovenkomt tegen kunnen komen. Als je een dertienjarige cyclus hebt, kun je alleen vijanden met een cyclus van één of dertien jaar elke keer tegenkomen. En een vijand met een cyclus van zes jaar kom je dan maar eens per 6 × 13 = 78 jaar tegen.
Cicaden richten overigens nauwelijks schade aan. Wel zijn ze imposant: op een vierkante kilometer kunnen wel een half miljoen beestjes uit de grond komen! Priemgetallen mogen misschien eenzaam zijn, cicaden zijn dat zeker niet.
 Internetbureau Rotterdam
Internetbureau Rotterdam 
