Dit bericht is geplaatst op maandag 6 juli 2009 om 09:45 in categorieën Column. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Bolmeetkunde
In Column, door Jeanine
Deze column verscheen in de Volkskrant van 4 juli 2009.
De meetkunde die je leert op school gaat over lijnen en driehoeken in het platte vlak. Je leert bijvoorbeeld dat de som van de hoeken van een driehoek altijd 180 graden is. Maar je kunt ook meetkunde bedrijven op andere objecten, op een bol bijvoorbeeld.

Als je met een vliegtuig van Amsterdam naar de Verenigde Staten vliegt, vlieg je vaak over Groenland. Op een landkaart ziet die route eruit alsof je in een rare bocht gevlogen bent, terwijl het toch de kortste route is. Dat komt doordat de aarde een bol is, en een boloppervlak is gekromd.
In het platte vlak zijn rechte lijnen de kortste routes. Om bolmeetkunde te kunnen doen, moeten we weten wat rechte lijnen zijn op een bol. De handigste definitie die we kunnen kiezen is gewoon dezelfde als die in het platte vlak: een rechte lijn tussen twee punten op een bol is de kortste afstand tussen die twee punten.
Op een bol blijken deze kortste afstanden stukken te zijn van zogenaamde grote cirkels. Dat zijn de grootst mogelijke cirkels die over een boloppervlak lopen. Als je een bol in tweeën zou snijden door een grote cirkel, dan snijd je precies door het middelpunt van de bol, en de twee stukken van de bol die je overhoudt zijn even groot. De evenaar is een grote cirkel op de aarde bijvoorbeeld, en de meridianen zijn halve grote cirkels.
In een plat vlak heb je altijd maar één kortste afstand tussen twee punten, maar op een bol is dat niet zo: de noord- en zuidpool worden verbonden door ontelbaar veel meridianen, die allemaal precies even lang zijn. Maar dat geeft niet, het geeft alleen aan dat bolmeetkunde echt anders is.
De definitie van een boldriehoek ligt nu voor de hand: drie punten die verbonden zijn door lijnstukken. Een voorbeeld van zo’n boldriehoek op aarde krijg je door de noordpool en twee verschillende punten op de evenaar te nemen, en de lijnen daartussen te trekken. Die lijnen zijn dan dus een stukje evenaar en twee halve meridianen.
Wat is in dit geval de som van de hoeken? De hoek tussen de evenaar en een meridiaan is 90 graden. In onze driehoek zitten dus al twee hoeken van 90 graden, en dan komt de hoek die de twee meridianen bij de noordpool vormen daar nog bij. De som is dus in ieder geval groter dan 180 graden! En dat geldt voor alle driehoeken op een bol. Teken maar eens wat driehoeken op een strandbal of ballon, als je het niet gelooft.
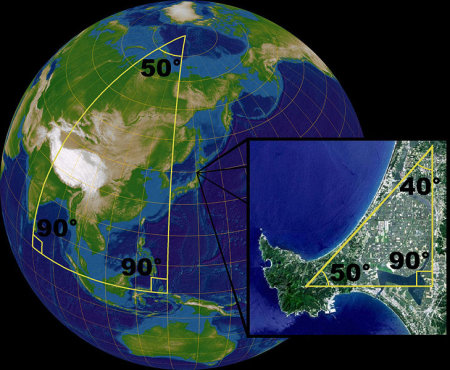
(Dit mooie plaatje komt van wikipedia.)
Onze aarde is zo groot, dat we van de kromming weinig merken en dat een driehoek die je in het zand tekent eigenlijk niet verschilt van die in een plat vlak. En dat is een ander bijzonder kenmerk van boldriehoeken: hoe groter de driehoek is ten opzichte van de hele bol, hoe groter het verschil is tussen de som van de hoeken en 180 graden! Iets om over na te denken als je deze zomer weer een strandbal op moet blazen.
 Internetbureau Rotterdam
Internetbureau Rotterdam 
