Internetbureau Rotterdam 
Dit bericht is geplaatst op dinsdag 4 augustus 2009 om 09:30 in categorieën Puzzels. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Jeanine op kamp (2)
In Puzzels, door Jeanine
Een vierkant is verdeeld in zeven stukken, waarmee je drie even grote vierkanten kunt leggen: een wit, een gestreept en een grijs vierkant. De zijde van het grote vierkant is 1.
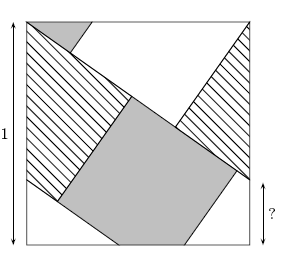
Een zijde van één van de stukken is met een vraagteken aangegeven. Hoe lang is die zijde?
