Internetbureau Rotterdam 
Dit bericht is geplaatst op woensdag 2 september 2009 om 10:00 in categorieën Algemeen, Puzzels. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Deelbaarheid door 7
In Algemeen,Puzzels, door Jeanine
Op de weblog van wiskundige Tanya Khovanova las ik een leuk stukje (er staan veel meer leuke stukjes op haar weblog!) over deelbaarheid door 7. Dit specifieke stukje is niet door haar zelf geschreven, maar door gastblogger David Wilson. Ik vertaal het hieronder.
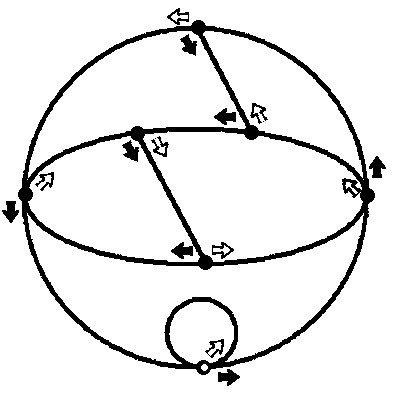
Deze graaf kun je gebruiken om te zien of een getal deelbaar is door 7. Schrijf een getal \(\) op. Begin bij de witte knoop helemaal onderin de graaf. Voor ieder cijfer \(\) in \(\), volg \(\) zwarte pijlen, en als je naar het volgende cijfer gaat, volg dan één witte pijl.
Bijvoorbeeld, als \(\), volg drie zwarte pijlen, dan een witte pijl, dan twee zwarte pijlen, dan weer een witte pijl en ten slotte vijf zwarte pijlen.
Als je weer uitkomt bij de witte knoop onderin, dan is \(\) deelbaar door 7, en anders niet.
Zoals Khovanova ook opmerkt: dat is niet het enige dat deze graaf doet. Je kunt uit deze graaf ook aflezen wat de rest van een getal is bij deling door 7. Maar het is leuker om dat zelf uit te zoeken. En kijk hier voor de interessante reacties op haar stukje.
woensdag 2 september 2009 om 10:12
Leuk, maar ik hou het toch maar op de staartdeling. Het is minder werk, je hebt er geen graaf bij nodig en je kunt het (bij delen door 7) uit je hoofd.
woensdag 2 september 2009 om 10:50
Heerlijk zo'n overdreven complexe graaf om eigenlijk iets heel eenvoudigs te doen. Ziet er ook lekker sci-fi uit, zou niet misstaan als een graancirkel, ofzo...
woensdag 2 september 2009 om 13:04
Mooi.. Aangezien deze graaf op triviale wijze om te vormen is naar een eindige toestandsautomaat is de taal "\(\) is deelbaar door 7" een reguliere taal. En zoals in de commentaren op de oorspronkelijke blog beschreven staat is het mogelijk zo een graaf voor elk deeltal op te stellen (al is die graaf niet altijd vlak). Dus al deze talen zijn regulier.
Maar uiteindelijk volgt dat waarschijnlijk al uit een staartdeling. :)
donderdag 3 september 2009 om 01:09
Heel erg leuk!
Wat geweldig bedacht, die graaf met twee soorten pijlen.
zaterdag 5 september 2009 om 20:01
[...] Wiskundemeisjes » Blog Archive » Deelbaarheid door 7 "Op de weblog van wiskundige Tanya Khovanova las ik een leuk stukje (er staan veel meer leuke stukjes op haar weblog!) over deelbaarheid door 7. Dit specifieke stukje is niet door haar zelf geschreven, maar door gastblogger David Wilson." (tags: dutch graph math) [...]