Internetbureau Rotterdam 
Dit bericht is geplaatst op vrijdag 15 januari 2010 om 09:38 in categorieën Uitjes. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Wiskundig wandelen in Nijmegen
In Uitjes, door Ionica
Al maanden geleden ontving ik een prachtig boekje van een Puzzelwandeling door historisch Nijmegen. Ik bedacht dat het leuk was om die wandeling zelf te maken voor ik er een stukje over schreef. Naïef als altijd dacht ik dat ik daar tijd genoeg voor had. Ik vergat even dat ik in die maanden mijn proefschrift af moest maken, terwijl ik al een nieuwe baan had en daarnaast freelance werk deed. Tel erbij op dat ik ook nog tien uur per nacht slaap nodig heb en dat zoals Wieb Bosma altijd zegt "de rest van Nederland nogal afgelegen ligt ten opzichte van Nijmegen". Kortom: ik ben nog steeds niet naar Nijmegen geweest, maar het is hoog tijd om iets over deze wandeling te schrijven. Dan kunnen lezers die in buurt van Nijmegen wonen (of die iets beter zijn in tijd-management) snel op een leuk uitje.
De wandeling is 6 km lang en duurt volgens de makers ongeveer 5 uur (ik gok dat je een flink deel van die tijd al puzzelend op terrasjes of in cafés doorbrengt). In het boekje staat informatie over de geschiedenis van Nijmegen en de gebouwen die je ziet. En natuurlijk een heleboel puzzelvragen. Dit is een voorbeeld van zo'n vraag.
De Sint Nicolaaskapel is het oudste gebouw van Nijmegen en een van de oudste van Nederland. Het werd omstreeks 1030 gebouwd en maakte deel uit van een grote burcht die de Duitse keizer Frederik Barbarossa in de 12de eeuw op het Valkhof liet bouwen. Het is een voorbeeld van Byzantijnse bouw. De centrale toren is achthoekig. Daaromheen is het gebouw zestienhoekig. Aan het dak is deze structuur goed te zien.
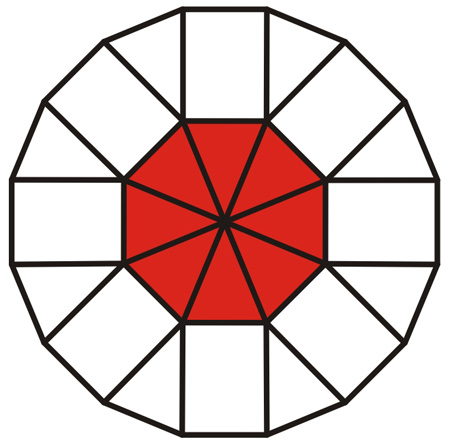
De acht- en zestienhoek zijn regelmatig. De omtrek van de zestienhoek is groter dan de omtrek van de rode driehoek. Hoeveel keer zo groot?
1 meer dan 2 keer
2. precies 2 keer
3. minder dan 2 keerDe oppervlakte van de witte ring van de zestienhoek is groter dan de oppervlakte van de rode achthoek. Hoeveel keer zo groot?
4. meer dan 3 keer
5. precies 3 keer
6. minder dan 3 keer
De wandeling is gemaakt door Leon van den Broek (onder andere bekend als organisator van Kangoeroe) en wiskundeleraar Lambert Kemerink. Op de site Puzzelwandeling Nijmegen vind je meer informatie. Het boekje is te koop voor 3 euro bij boekhandels en VVV in Nijmegen. Je kunt het boekje ook bestellen via de site.
vrijdag 15 januari 2010 om 10:06
Ik heb deze wandeling al gemaakt (een paar maanden geleden) en kan hem aanraden voor iedere puzzel-liefhebber of historicus.
Kijk tijdens de wandeling goed om je heen (zeker in de kleine steegjes), want er zijn veel interessante/grappige dingen te zien. Zo kom je langs een muur vol met vogelhuisjes die je niet zal zien als je je focust op de route.
vrijdag 15 januari 2010 om 14:43
ITYM "De omtrek van de zestienhoek is groter dan de omtrek van de rode achthoek."
vrijdag 15 januari 2010 om 18:33
Best leuke opgaves! Maar ik moest langer denken over wat Speicus schreef.
@speicus. Ik zie wat je bedoelt. Bij de eerste opgave staat inderdaad *rode driehoek* waar *rode achthoek* moet staan. En: I Think You Mean I Think You Mean When You Write ITYM.
zaterdag 16 januari 2010 om 16:06
De wandeling met de vogelhuisjes is iets te ver weg, dan maar even puuselen:
Parallelle korte zijden van rechthoek zijn gelijk, en zestienhoek is regelmatig ==> "precies 2 keer". ==> Witte driehoek is gelijk (zijde en hoeken) aan rode, in de hele figuur komen dus maar twee verschillende lengtes voor. Opp.rechthoek > opp.parallellogram ==> "meer dan 3 keer".
maandag 18 januari 2010 om 11:11
Denk nog eens goed na Zaaikort
maandag 18 januari 2010 om 12:02
Volgens mij heeft Zaaikort al goed nagedacht en heeft hij gelijk. twee driehoeken met de langste zijde tegen elkaar gelegd vormen een parallellogram met een oppervlakte die kleiner is dan de oppervlakte van de rechthoek. Dat is meetkundig direct duidelijk.
maandag 18 januari 2010 om 14:39
Rinse, er zijn exact 2 driehoeken nodig om een rechthoek met dezelfde base bedekken. Niet meer en niet minder. Denk daarvoor maar aan de formule Basis*hoogte/2 voor de driehoeksoppervlakte en basis*hoogte voor de rechthoeksoppervlakte.
Er zijn 8 rode driehoeken, 8 witte driehoeken, en 8 rechthoeken. 1 rechthoek staat gelijk aan 2 driehoeken, dus 8(witte driehoeken) + 8(witte rechthoeken)*2(aantal driehoeken per rechthoek) = 24 driehoeksoppervlakten. De oppervlakte van de band is dus exact drie keer die van de rode achthoek.
maandag 18 januari 2010 om 14:39
Verdorie, de spoiler te vroeg geeindigd -.-'
maandag 18 januari 2010 om 14:50
@Matthias: dit klopt niet helemaal. Merk op dat de driehoeken niet rechthoekig zijn, en dat hun basis (tegenover de tophoek) precies gelijk is aan de korte zijde van een rechthoek. Elk van de benen van de driehoek is gelijk aan de lange zijde van een rechthoek. Als je dan in de oppervlakteformule voor een driehoek één van de benen als basis neemt, dan is de hoogte dus net iets kleiner dan de korte zijde van een rechthoek. Ergo: de oppervlakte van een rechthoek is net iets meer dan die van twee driehoeken. De oppervlakte van de witte ring is dus iets meer dan drie keer zo groot als die van de rode achthoek.
woensdag 20 januari 2010 om 10:08
@ Matthias: De hoogte van een rechthoek is meer dan de hoogte van een driehoek.
zaterdag 30 januari 2010 om 20:04
[...] Wiskundig wandelen in Utrecht, Amsterdam of Nijmegen [...]
vrijdag 9 april 2010 om 11:37
[...] naar Nijmegen voor een paar workshops en … de puzzelwandeling, waar Ionica al eerder een leuk stukje over [...]
vrijdag 11 januari 2019 om 14:26
Er valt niet meer aan dit boekje te komen, helaas....
Zou hem toch graag een keer lopen, met Ionica bijvoorbeeld ;-)