Dit bericht is geplaatst op donderdag 4 maart 2010 om 10:09 in categorieën Puzzels. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
De aarde aan een spijker
In Puzzels, door Ionica
Een tijdje terug schreef ik een stukje over wat er gebeurt als je een touw strak om de aarde spant, er een meter touw bij doet en vervolgens het touw overal evenver optilt. Zie ook dit filmpje.
In de reacties op dat stukje stelde Koen als verdiepingsvraag: "En als je dat touwtje nou aan een kant aantrekt, zodat er een punt ontstaat en aan de andere kant van de aarde het touw weer strak om de aarde zit, hoe hoog wordt die punt dan?"
Lezers Robert Groenewold en Lon Boonen brachten een lange avond in de kroeg door om deze vraag op te lossen. Ze stuurden onderstaande oplossing in. Wij vertellen ze maar niet dat dit alles al lang op de site van KP Hart te vinden was...
Onlangs spanden de wiskundemeisjes een touw strak om de aarde om het vervolgens een meter langer te maken en aan te tonen dat zelfs een lineair verband (tussen straal en omtrek) contra-intuïtief kan zijn. Aangezien allle moeite reeds gedaan is om genoemd touw te spannen wilden wij, twee natuurkundejongens, dat touw een alternatieve bestemming geven.
Wanneer we een touw strak rond de aarde spannen, één meter touw toevoegen en het geheel aan een spijkertje ophangen, wat is dan de afstand tussen de aarde en het spijkertje? Past de Domtoren er onder?
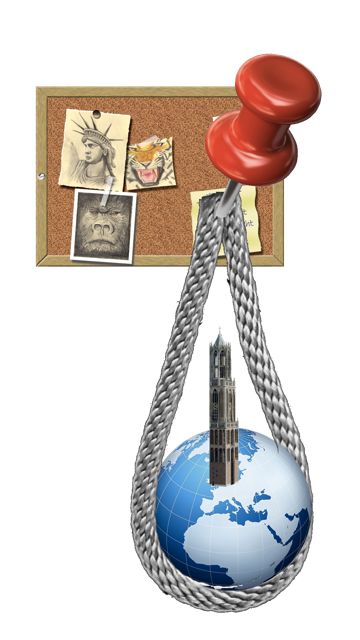
De oplossing kostte ons een avond in (het helaas ter ziele gegane) Ledig Erf in Utrecht. En ettelijke bierviltjes. Deels was dit te wijten aan het feit dat we (schaam, schaam) de Taylor-reeks opnieuw moesten ontdekken.
Daar gaan we... We zien twee rechthoekige driehoeken die gevormd worden door het centrum van de aarde, het spijkertje en het punt waar het touw de aarde raakt. We bekijken één van die driehoeken.
De hoek onder de grond noemen we α. We veronderstellen dat α klein is en dat is ook zo. Van de middelbare school konden we ons nog SOS, CAS en TOA herinneren.
De lengten van deze zijden zijn als volgt:
S = Schuine zijde = R + h, waarbij R de straal van de aarde is en h de raadselachtige hoogte
A = Aanliggende rechthoekzijde = R
O = Overstaande rechthoekzijde = αR + ½
Laten we eerst de tangens te grazen nemen:
tan(α) = (αR + ½)/R = α + ½/R
Nu moesten we Taylor om hulp vragen. Gelukkig hebben we tegenwoordig Wolfram Alpha, twee termen leek ons ruim voldoende:
tan(α) = α + α3/3
Dat komt goed uit:
α = 3√1½R.
Dan nu de cosinus:
cos(α) = R/(R+h)
Ofwel:
h = R(1/cos(3√1½R) - 1)!
Vul je alles netjes in, dan kom je op een h van 121m. Ruim voldoende voor de Domtoren dus!
Ik heb 'm ook effe geïnverteerd: voor een h van 2m heb je een extra stukje touw van 2mm nodig! Dus als de wiskundemeisjes hun touw per ongeluk 2mm te lang hadden gemaakt (op de 40.000km), dan had je het touw tussen duim en wijsvinger op kunnen tillen en er onderdoor kunnen stappen als bij een hek met prikkeldraad.
Hoe we het al die jaren geleden precies hebben gedaan hebben we niet kunnen achterhalen... Een derdemachtswortel trekken en een cosinus berekenen zijn zover ik weet niet triviaal op een bierviltje. Hoewel ik ook weer hoor dat je dat allemaal met wat origami prima voor elkaar krijgt.
(Robert Groenewold en Lon Boonen)
 Internetbureau Rotterdam
Internetbureau Rotterdam 
