Wiskundemeisjes

Ludolph van Ceulen

Deze column verscheen vandaag in de Volkskrant.

Als je wil weten hoe de decimalen van het getal pi (de verhouding tussen de omtrek en de diameter van een cirkel, ongeveer gelijk aan 3,14159265…) er uitzien, hoef je tegenwoordig alleen maar je rekenmachine te pakken of je computer aan te zetten. Dat was in de zeventiende eeuw wel anders. Ook toen was men geïnteresseerd in pi.

Ludolph van Ceulen

Het rekenwerk in die tijd lijkt mij geen pretje, maar scherm- en rekenmeester Ludolph van Ceulen (1540 – 1610) dacht daar heel anders over. Hij berekende pi tot maar liefst 35 decimalen. Zijn methode, naar een idee van Archimedes, komt neer op het volgende principe. Een cirkel met diameter 1 heeft een omtrek van lengte pi. Je kunt nooit een cirkel zó precies tekenen en meten dat je op die manier pi redelijk kunt benaderen.

Teken nu in een cirkel met diameter 1 een vierkant dat nog nèt in de cirkel past, en teken om die cirkel heen een vierkant zodat de cirkel precies aan de vier zijden raakt. Dan zit de omtrek van de cirkel tussen de omtrek van het kleine en die van het grote vierkant in. En omtrekken van vierkanten kun je makkelijk uitrekenen.

Bij een cirkel met diameter 1 vind je zo de volgende benadering van pi: 2√2 < pi < 4. Het getal 2√2 is ongeveer 2.82842712, dus dit geeft geen goede benadering. Maar als je in plaats van vierkanten regelmatige veelhoeken met veel meer hoeken in en om de cirkel past, en daar de omtrekken van uitrekent, krijg je steeds betere onder- en bovengrenzen voor pi.

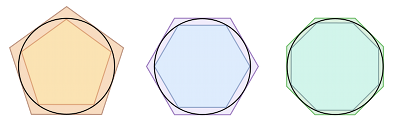
Archimedes gebruikte regelmatige 96-hoeken en vond dat 3.140909654 < pi < 3,142826575. Van Ceulen ging veel verder en gebruikte regelmatige 32.212.254.720-hoeken. Daarmee vond hij 20 decimalen. Hij moet een veelhoek met nog meer hoeken gebruikt hebben voor zijn 35 decimalen, maar we weten niet welke. Een hele prestatie, als je bedenkt dat hij daarvoor talloze wortels moest trekken, met ook extreem veel decimalen om nauwkeurig genoeg verder te kunnen rekenen, en dat met de hand… Met zijn benaderingen kon Van Ceulen en passant een aantal geleerde tijdgenoten die claimden oplossingen van de cirkelkwadratuur gevonden te hebben, op hun nummer zetten. De vraag daarbij is om, gegeven een cirkel van een bepaalde grootte, een vierkant te construeren dat dezelfde oppervlakte heeft. Dat is een onmogelijke opdracht, en de crux zit in het woord “construeren”: je mag alleen een passer en een latje (een liniaal zonder schaalverdeling) gebruiken. In 1882 werd definitief bewezen dat het probleem onoplosbaar is, maar in de zeventiende eeuw wist men dat nog niet zeker. Van Ceulen kon met zijn benaderingen van pi wel laten zien dat de geclaimde oplossingen allemaal fout waren!

Hij was erg trots op zijn prestatie, en daarom kwamen de 35 decimalen op zijn grafsteen terecht. Dat was de eerste keer dat al die decimalen gepubliceerd werden. In de Leidse Pieterskerk is een replica te zien. Dit jaar is Van Ceulen vierhonderd jaar dood, dus laten we op pi-dag (14 maart, naar 3,14) maar eens aan zijn gereken denken!

Edit: neem ook eens een kijkje op www.ludolphvanceulen.nl.