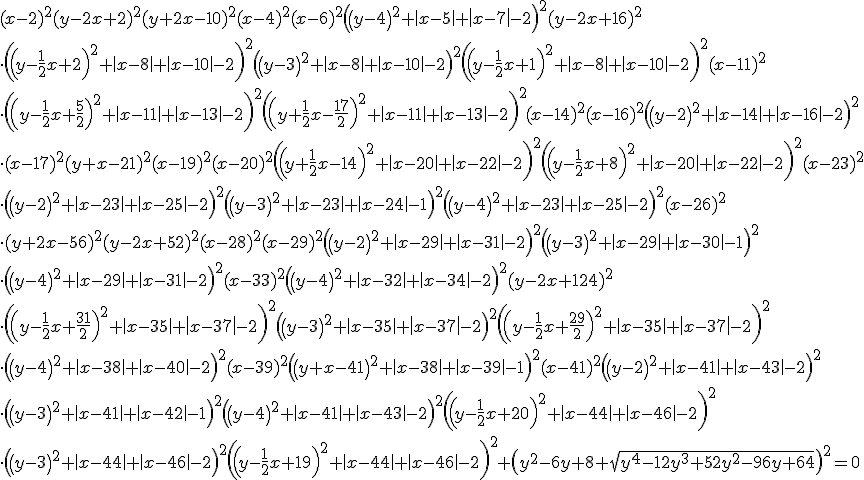webhost van wiskundemeisjes.nl 
Dit bericht is geplaatst op Tuesday 9 March 2010 om 09:00 in categorieën Algemeen. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Gave formule
In Algemeen, door Ionica
Wie kan er raden wat er zo gaaf is aan deze formule?
(Klik voor een vergroting)
Als jullie er niet uitkomen, dan zal ik later deze week het antwoord geven. Maar ik hoop dat het niet nodig is.
Tuesday 9 March 2010 om 10:13
Ik ben er nog niet maar, voor reëele oplossingen
moet y gelijk zijn aan 2 of 4, alleen dan is de laatste term 0.
Tuesday 9 March 2010 om 10:20
Zo op het eerste zicht zijn het de “wiskundemeisjes”.
Tuesday 9 March 2010 om 10:25
Ik gok dat je de formule moet plotten, maar ik heb hier geen software voor bij de hand..
Tuesday 9 March 2010 om 11:02
Ik heb het idee dat elk volgend deel van de formule wordt bepaald door het voorgaande maar ik zie nog niet hoe. De constanten lopen vrij regelmatig op.
Tuesday 9 March 2010 om 11:15
Bedoel je iets anders dan dat het niet uitmaakt wat y is, als x=2?
Tuesday 9 March 2010 om 12:13
For the fact that every factor in the products of the first term are squared as well as the second term I deduced that for real solutions,
or 
and from there it’s possible to derive the 
such that the first term equals 0 I don’t have all of ‘em yet. I also finding the complex solutions
Tuesday 9 March 2010 om 12:14
(Sorry, didn’t know LaTeX aren’t covered :S
Tuesday 9 March 2010 om 12:37
Ik ben niet zo wiskundig, maar dit valt mij op:
De getallen 9-12-15-18 ontbreken, evenals 27 (3*9), 36 (3*12), 45 (3*15) en waarschijnlijk 54 (3*18)
Nu ga ik het even helemaal uitrekenen… ;-)
Tuesday 9 March 2010 om 13:41
Ik zou de term $(y-2x+16)^2$ (de laatste term op de eerste regel) vervangen door $((y-2)^2-|x-5|+|x-7|-2)^2$.
Tuesday 9 March 2010 om 13:54
En ook de term
op de zevende regel zou ik vervangen door 
.
Tuesday 9 March 2010 om 15:57
Een gok:
Iets met pi misschien?
Tuesday 9 March 2010 om 22:07
Inverse graphing, neem ik aan?
Tuesday 9 March 2010 om 22:09
Maple faalt bij het plotten van het woord. :(
Tuesday 9 March 2010 om 23:27
een wiskundige manier om wiskundemeisjes te schrijven bien sûr ;-))
Wednesday 10 March 2010 om 11:38
Wat ik zie:
kwadraat*kwadraat*kwadraat*…*kwadraat + kwadraat = 0
Best knap als je bedenkt dat kwadraten 0 of groter zijn.
Wednesday 10 March 2010 om 14:29
Tussen y=2 en y=4 is de laatste term altijd gelijk aan 0. De eerste term is voor een aantal x-waarden (zoals x=2, x=4, x=6 etc.) gelijk aan 0, deze vergelijking heeft dus een oneindig aantal nulpunten.
Wednesday 10 March 2010 om 15:25
Scherp opgemerkt Ton, het laatste teken is een plus! Die had ik eerst niet gezien.. Dat maakt het een heel ander verhaal, moeilijker vermoed ik. Ik ben benieuwd naar de onthulling.
Wednesday 10 March 2010 om 16:08
Ik denk dat dit er staat, maar ik kan het niet goed lezen:
00101010110100111101100111111111010100010111100000000000000000010
00101010111100100111101110101110010111110110111000000000000000000
00111111001101100101100111101111111001111100001000000000000000001
Wednesday 10 March 2010 om 16:31
Wat ik gedaan heb is alle oplossingen voor gehele getallen (0
x 
64; 2 
y 
4) uitrekenen. Oplossingen zijn bijvoorbeeld: {2,2}, {2,3} en{5,4}.
De drie strings hierboven zijn voor y = 2, 3 en 4.
Plot de strings en het ziet eruit als een woord, misschien begint het met een W.
Ik heb het ook al op de kop geplot, dan lijkt het een woord dat met een M begint.
Wednesday 10 March 2010 om 16:46
En dan vergeet ik nog de antwoorden {256, 2}, {256, 3} en {256, 4}.
Misschien is het iets met ASCII ofzo.
Maar wellicht vergis ik me, heb ik een typfoutje gemaakt met m’n dyslexie.
Weet er hier iemand een goede Optical Character Recognizer voor wiskundeformules?
Wednesday 10 March 2010 om 16:51
Ha, ik heb het goede antwoord al gezien! Wie zelf nog even wil puzzelen, hier is een kopiëerbare versie van de formule:
(x-2)^2(y-2x+2)^2(y+2x-10)^2(x-4)^2(x-6)^2((y-4)^2+|x-5|+|x-7|-2)^2(y-2x+16)^2((y-(1/2)x+2)^2+|x-8|+|x-10|-2)^2((y-3)^2+|x-8|+|x-10|-2)^2((y-(1/2)x+1)^2+|x-8|+|x-10|-2)^2(x-11)^2((y-(1/2)x+(5/2))^2+|x-11|+|x-13|-2)^2((y+(1/2)x-(17/2))^2+|x-11|+|x-13|-2)^2(x-14)^2(x-16)^2((y-2)^2+|x-14|+|x-16|-2)^2(x-17)^2(y+x-21)^2(x-19)^2(x-20)^2((y+(1/2)x-14)^2+|x-20|+|x-22|-2)^2((y-(1/2)x+8)^2+|x-20|+|x-22|-2)^2(x-23)^2((y-2)^2+|x-23|+|x-25|-2)^2((y-3)^2+|x-23|+|x-24|-1)^2((y-4)^2+|x-23|+|x-25|-2)^2(x-26)^2(y+2x-56)^2(y-2x+52)^2(x-28)^2(x-29)^2((y-2)^2+|x-29|+|x-31|-2)^2((y-3)^2+|x-29|+|x-30|-1)^2((y-4)^2+|x-29|+|x-31|-2)^2(x-33)^2((y-4)^2+|x-32|+|x-34|-2)^2(y-2x+124)^2((y-(1/2)x+(31/2))^2+|x-35|+|x-37|-2)^2((y-3)^2+|x-35|+|x-37|-2)^2((y-(1/2)x+(29/2))^2+|x-35|+|x-37|-2)^2((y-4)^2+|x-38|+|x-40|-2)^2(x-39)^2((y+x-41)^2+|x-38|+|x-39|-1)^2(x-41)^2((y-2)^2+|x-41|+|x-43|-2)^2
((y-3)^2+|x-41|+|x-42|-1)^2((y-4)^2+|x-41|+|x-43|-2)^2((y-(1/2)x+20)^2+|x-44|+|x-46|-2)^2((y-3)^2+|x-44|+|x-46|-2)^2((y-(1/2)x+19)^2+|x-44|+|x-46|-2)^2+(y^2-6y+8+sqrt(y^4-12y^3+52y^2-96y+64))^2=0
Wednesday 10 March 2010 om 16:54
De aanpassingen van Jos zijn inderdaad veel beter. Nu ziet het er wat vreemd uit met die t’s en die doorstreepte letter.
Wednesday 10 March 2010 om 17:36
@Googol: het wordt vast de oplossing van Wie is de Mol!
Wednesday 10 March 2010 om 18:18
@suzan
Uhm, wat is dat precies, “Wie is de Mol” ? :-(
Beetje dom van me om alleen naar discrete oplossingen te kijken :-)
Wednesday 10 March 2010 om 18:58
Gefeliciteerd, Jan, Jos, Tim en ptityeti!
Probeer ik indruk te maken op de wiskundemeisjes,
terwijl jullie de oplossing allang gevonden hebben.
Thursday 11 March 2010 om 22:28
http://www.xamuel.com/inverse-graphing-calculator.php voor wie het zelf eens wil proberen. :)
Saturday 20 March 2010 om 16:31
het is gewoon een lekker ding
Monday 22 March 2010 om 01:31
Leuk stukje van gemaakt!