Internetbureau Rotterdam 
Dit bericht is geplaatst op vrijdag 12 maart 2010 om 09:59 in categorieën Algemeen. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Plaatjesbewijs
In Algemeen, door Jeanine
Ik houd van plaatjesbewijzen: plaatjes die zo duidelijk het idee van het bewijs weergeven dat er nauwelijks of geen woorden meer nodig zijn. Op deze lijst op mathoverflow.net staan er een heleboel. Ik licht er voor jullie één mooi idee uit.
Een vierkant van 8x8 kun je precies bedekken met dominosteentjes van 1x2 veldjes. Kan dat nog steeds als je het veldje in de linkerbovenhoek en het veldje in de rechteronderhoek verwijdert? Het antwoord is nee, en het argument is als volgt (als spoiler voor de mensen die er eerst zelf over willen nadenken). Stel je het 8x8-vierkant voor als een schaakbord. Hoe je een dominosteentje ook op het schaakbord legt zodat het precies twee vakjes bedekt, je bedekt altijd een wit én een zwart vakje.
De twee vakjes die zijn verwijderd van het schaakbord hadden allebei dezelfde kleur (wit), dus nu zijn er meer zwarte dan witte vakjes over. Als het schaakbord nog gevuld zou kunnen worden met dominosteentjes, dan zouden er evenveel witte als zwarte velden bedekt zijn, maar er zijn niet evenveel witte als zwarte velden. Dus dat kan niet.
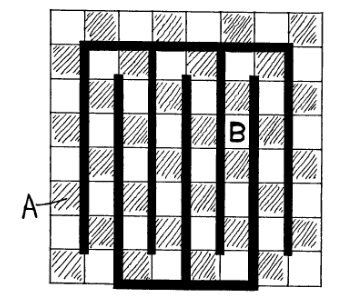
Een opvolgende vraag is nu: als je nou niet twee vakjes van dezelfde kleur weghaalt, maar willekeurig één wit en één zwart vakje, kun je het bord dan wèl altijd vullen met dominosteentjes? Het antwoord ligt niet meteen voor de hand, maar onderstaand plaatje laat zien dat dat inderdaad kan. Dit bewijs is van Ralph E. Gomory, en het plaatje komt van deze site.
