Dit bericht is geplaatst op zaterdag 10 juli 2010 om 09:38 in categorieën Column. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Wat ik de afgelopen jaren deed
In Column, door Ionica
Deze column verscheen vandaag in de Volkskrant. Op deze blog heb ik trouwens al vaker over kettingbreuken geschreven
“Waarom schrijf je nooit eens een column over je eigen onderzoek?”, vroeg mijn promotor de week voor de verdediging van mijn proefschrift. De afgelopen jaren stond een groot deel van mijn leven in het teken van kettingbreuken, het onderwerp van mijn promotie-onderzoek. Dat onderzoek viel me soms zwaar, het was traag en eenzaam werk. En als ik dan eindelijk een nieuw resultaat bewezen had, dan kon ik aan bijna niemand uitleggen wat ik had bereikt. Daarom schreef ik hier liever over andere, meer toegankelijke onderwerpen.
Inmiddels heb ik mijn proefschrift met succes verdedigd en de komende jaren zal ik waarschijnlijk geen zwaar theoretisch wiskundig onderzoek meer doen. En nu besef ik ineens wat ik ga missen: samen met enthousiaste collega’s voor een schoolbord een nieuw idee uitwerken, op de fiets naar huis ineens begrijpen hoe het bewijs moet lopen en het gevoel van ultieme triomf als alle details keurig op hun plaats schuiven. Daarom deze week een stukje over die kettingbreuken waar ik jaren aan werkte. Omdat ik ze stiekem nu al een beetje mis.
Ceci n'est pas une kettingbreuk
Allereerst: een kettingbreuk heeft niets te maken met gestrande wielrenners of vastgelopen machines. Het is in feite een ketting van breuken: een breuk in een breuk in een breuk (enzovoorts), zie het plaatje hieronder voor de kettingbreuk van pi. Elk getal kun je schrijven als een kettingbreuk. Voor breuken krijg je een eindige kettingbreuk. Voor getallen die zelf geen breuk zijn, zoals pi, is de bijbehorende kettingbreuk oneindig lang.
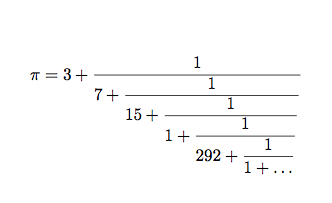
Als je zo’n oneindige kettingbreuk afkapt door het onderste stuk vanaf een zeker punt weg te laten, krijg je een gewone breuk. Op die manier kun je oneindige reeks benaderingsbreuken voor je oorspronkelijke getal vinden. Neem bijvoorbeeld de kettingbreuk van pi. Als je alles onder de 7 vergeet, dan krijg je 3 + 1/7, oftewel 22/7, een benadering van pi die vroeger vaak op school werd gebruikt. De volgende benadering krijg je door alles na 15 te vergeten: dit geeft 333/106. En door nog één term verder te gaan, vind je 355/113. Die laatste breuk is ongeveer 3,14159292 en benadert pi tot op maar liefst zes decimalen. Deze benadering is zo goed, dat geen enkele breuk met noemer kleiner dan 16604 dichter bij π ligt. De Chinese wiskundige Chong Zhi berekende deze goede benadering voor pi trouwens al rond 480 na Christus, maar hij deed dat zonder kettingbreuken.
Goede benaderingen zijn breuken met een kleine noemer die heel dicht bij het oorspronkelijke getal liggen. En zulke benaderingen worden precies gevonden met kettingbreuken. Kettingbreuken hebben allerlei toepassingen, maar dat is niet de reden dat ik ze jarenlang bestudeerd heb. Ik werkte aan een generalisatie van de kettingbreuken en probeerde daarmee heel algemene eigenschappen te bewijzen. Ik wilde bijvoorbeeld weten hoeveel benaderingen je achter elkaar moet nemen om zeker te weten dat er een heel goede tussen zit. Als zo’n algemeen bewijs na lang zwoegen lukte, dan vielen een heleboel puzzelstukjes op hun plaats en was ik even het gelukkigste wiskundemeisje op aarde.
 Internetbureau Rotterdam
Internetbureau Rotterdam 
