Internetbureau Rotterdam 
Dit bericht is geplaatst op donderdag 19 augustus 2010 om 10:00 in categorieën Puzzels. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Jeanine op kamp (4)
In Puzzels, door Jeanine
Ingeschreven vierkant
Een driehoek heeft zijdes van lengte 10, 17 en 21. Binnen de driehoek hebben we een vierkant, waarvan één van de zijden op de langste driehoekszijde staat, en de andere hoekpunten raken de andere twee driehoekszijdes.
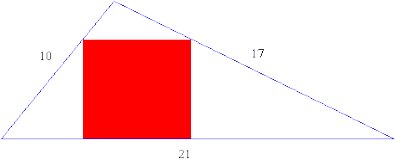
Wat is de lengte van de zijde van het vierkant?
