Wiskundemeisjes

Deze column verschijnt vandaag in De Volkskrant.

Van wiskunde op de middelbare school herinneren veel mensen zich maar twee dingen: de stelling van Pythagoras en de wanhopige vraag waar al die sommen goed voor zijn. Mijn eigen wiskundedocent had helaas nooit een erg bevredigend antwoord op die vraag. En dat terwijl je alleen de stelling van Pythagoras al kunt gebruiken bij het maken van een boomhut of het bestellen van pizza’s.

De eeuwenoude stelling gaat over een rechthoekige driehoek. In zo’n driehoek is het kwadraat van de lengte van de schuine zijde gelijk aan de kwadraten van de lengtes van de twee rechthoekszijden bij elkaar opgeteld. Oftewel: (waarbij en de lengtes van de rechtshoekzijden zijn en de lengte van de schuine zijde).

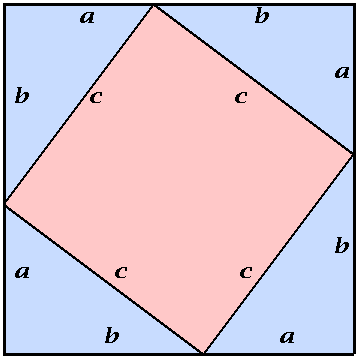
Een plaatjesbewijs voor de stelling van Pythagoras

Op school wordt de stelling vooral gebruikt om de lengte van zijden te bepalen in allerlei driehoeken, parallellogrammen en andere figuren. Maar de stelling van Pythagoras kan ook nuttig zijn bij meer alledaagse problemen, bijvoorbeeld bij het maken van een boomhut (of een hekje, of een schuurtje). Ze helpt je namelijk om zonder geodriehoek of winkelhaak een perfecte rechte hoek te construeren. Je hebt alleen een stukje touw nodig, een mes en iets om mee te meten. Snijd drie stukken touw af van 30, 40 en 50 centimeter en leg deze stukken in een driehoek. De hoek tussen de stukken van 30 en 40 centimeter is nu een rechte hoek, dus daarmee kun je je de wanden van je boomhut keurig haaks op elkaar spijkeren. De driehoek van touw heeft zijden van 30, 40 en 50 centimeter en (dus ).

Scherpe lezers zullen opmerken dat je eigenlijk niet eens touw nodig hebt voor deze truc. Alleen iets om te te meten is ook al genoeg. Nog scherpere lezers zullen opmerken dat hierbij niet de stelling van Pythagoras wordt gebruikt, maar haar omkering. Als namelijk in een driehoek met zijden en geldt dat , dan is het een rechthoekige driehoek. Dat vertellen ze helaas bijna nooit op de middelbare school.

En wat ze al helemaal niet vertellen is dat je de formule ook kunt gebruiken voor andere vormen dan driehoeken, bijvoorbeeld voor cirkels. Stel dat je in een pizzeria twijfelt: op de kaart staan pizza’s met een diameters van 18, 24 en 30 centimeter. Je bent met een groep en vraagt je af of je beter twee kleine pizza’s kunt nemen of één grootte. Maar dan bedenk je dat . En dat betekent dat de twee pizza’s van 18 en 24 centimeter samen precies even groot zijn als één pizza van 30 centimeter (reken het maar na). Waarschijnlijk ben je een stuk goedkoper uit met één grote pizza. Daar is wiskunde dus goed voor.

Deze column verschijnt vandaag in de Volkskrant.

Een tijdje geleden deed ik een “wisquiz” met mijn brugklasleerlingen. Ik stelde onder andere de vraag: wat zijn de drie volgende getallen in het rijtje 1, 4, 9, 16, … ?

Nou kun je strikt gezien bij elke willekeurige drie volgende getallen een wiskundige regel verzinnen die precies die getallen oplevert, maar mijn leerlingen gingen druk op zoek naar een niet al te ingewikkeld patroon, en ze vonden er een. Àlle groepjes noemden als volgende drie getallen 25, 36 en 49. Bij navraag naar het patroon dat ze gevonden hadden, zeiden ze: “Nou, eerst hebben we 1, dan doe je er 3 bij, dan 5, dan 7 en zo verder, dus je doet steeds het volgende oneven getal erbij.” Klopt helemaal.

Maar misschien denkt u verbaasd: “Hè, maar dat zijn toch gewoon de kwadraten?” Klopt ook: 1² = 1, 2² = 4, 3² = 9 en 4² = 16. Dat is grappig. Mijn brugklasleerlingen hadden nog niet geleerd wat een kwadraat is. Wat blijkbaar hun gebruikelijke aanpak is bij zo’n rijtjes-afmaak-som, is kijken naar de verschillen tussen opeenvolgende getallen en of daar een duidelijke regelmaat in zit. En die hadden ze gevonden.

Nou is het op het eerste gezicht best gek dat de regelmaat van mijn leerlingen (steeds het volgende oneven getal erbij optellen) en de regelmaat die mijzelf onmiddellijk in het oog springt (de rij van kwadraten) dezelfde drie volgende getallen opleveren. Dus dan kun je je afvragen: is dat toeval? Of geven deze twee manieren ook bij het vierde, vijfde, zesde, en honderdmiljoenste getal dezelfde antwoorden?

Bij de regel van mijn leerlingen tel je achtereenvolgens bij het getal 1 op: 3, 5, 7, 9, enzovoorts. Het achtste getal in het rijtje is dus de som (optelling) van de eerste acht oneven getallen. Algemeen geformuleerd: het n-de getal in het rijtje is de som van de eerste n oneven getallen, wat voor nummer n ook is. Maar als we het rijtje voortzetten met de kwadratenregel, is het n-de getal in het rijtje het kwadraat van het getal n, oftewel n².

De vraag is dus: zijn die rijtjes inderdaad hetzelfde, oftewel: is de som van de eerste n oneven getallen gelijk aan n², voor alle n? Ja, dat is zo, en het is zelfs redelijk eenvoudig om in te zien waarom! Een simpele serie plaatjes laat zien wat er gebeurt.

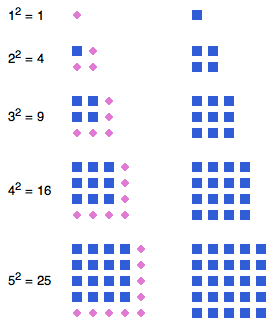
We beginnen met het getal 1: dat ene roze vierkantje linksboven. Vervolgens tellen we daar 3 bij op, in het plaatje daaronder aangegeven door drie roze vierkantjes. Die drie vierkantjes zijn zó neergelegd, dat er precies een vierkant van 2 bij 2 ontstaat, dus je ziet meteen dat daar 2² vierkantjes liggen. En zo gaan we verder. Als er een vierkant ligt van n bij n vierkantjes, dat dus uit n² vierkantjes bestaat, dan moeten we n + n + 1, oftewel 2n+1 vierkantjes erbij leggen om het volgende kwadraat te leggen. En 2n+1 is precies het volgende oneven getal.

Maakt u zich trouwens vooral geen zorgen: inmiddels weten mijn leerlingen ook wat kwadraten zijn.