Wiskundemeisjes

Deze column verschijnt vandaag in De Volkskrant.

Eens in de zoveel tijd krijg ik een brief van een onbekende die beweert dat hij een beroemd wiskundig probleem heeft opgelost. Vaak is de toon van de brief zelfingenomen, de notatie onnavolgbaar en het bewijs onjuist. Ik vind het altijd lastig om te reageren op dit soort brieven. Het kost ontzettend veel tijd om de onorthodoxe redeneringen te volgen en nog meer tijd om er een zinvolle reactie op te geven. Het is verleidelijk om dat soort brieven maar gewoon te negeren. Maar ik vind het tegelijk belangrijk om buitenstaanders serieus te nemen en te laten zien dat wiskundigen niet in een ivoren toren zitten. Daarnaast is er altijd de kleine kans dat je het werk van een genie in de prullenbak gooit.

Hier zouden wiskundigen het bewijs van de Riemann-hypothese kunnen vinden, als ze hun oogkleppen eindelijk eens afdeden

De in 1947 overleden wiskundige G.H. Hardy liet de wiskundige gemeenschap veel na: een hele reeks resultaten en het prachtige boekje Apologie van een wiskundige (dat deze maand overigens voor het eerst in het Nederlands verschijnt). In die apologie betoogt Hardy dat wiskunde alleen voor jonge mensen is en dat echte wiskunde nutteloos is. Die twee ideeën leven nog steeds onder veel wiskundigen.

Maar Hardy’s belangrijkste verdienste is waarschijnlijk dat hij het genie in Srinivasa Ramanujan herkende. De Indiër Ramanujan raakte als scholier in de ban van wiskunde. Hij blonk uit, maar verwaarloosde zijn andere vakken zo erg dat hij de universiteit moest verlaten. Uiteindelijk vond hij een baantje als klerk en deed hij wiskunde in zijn vrije tijd.

De Indiase klerk schreef rond 1913 verschillende Britse wiskundigen over zijn ontdekkingen. Eén professor antwoordde dat Ramanujan wel aanleg had voor wiskunde, maar de basis miste om door andere wiskundigen geaccepteerd te worden. Twee anderen stuurden zijn brief zonder commentaar terug. In eerste instantie legt ook G.H. Hardy de brief van Ramanujan terzijde. De vellen stonden vol bizar uitziende formules, een enkele daarvan was al bekend. Nergens stonden bewijzen. In een latere brief van Ramanujan stond bijvoorbeeld de op het eerste gezicht absurde conclusie dat 1+2+3+4+… = -1/12 (wat na jaren wiskundige studie wel degelijk een zinvolle vergelijking blijkt).

Ramanujan tussen een aantal van zijn formules

De gewaagde stellingen van Ramanujan zetten Hardy aan het denken. De Indiër moest óf een geniale bedrieger zijn, óf een onontdekte wiskundige. Hij besloot dat de kans op een zo slimme bedrieger wel heel klein was en haalde Ramanujan naar Engeland. Ramanujan bleek inderdaad zeer getalenteerd: Hardy vergeleek hem met grote namen als Euler, Gauss, Newton en Archimedes. Tragisch genoeg overleed Ramanujan al op zijn drieëndertigste. (Het moet voor Hardy een schrale troost zijn geweest dat hij geloofde dat wiskundigen hun beste werk doen vóórdat ze dertig zijn.)

Het talent van Ramanujan is een extreme zeldzaamheid. Ik vind het knap dat Hardy de brief van de Indiër ontdekte tussen de stapel onzinnige brieven die hij kreeg. Ik weet zeker dat ik de briljantie van Ramanujan niet zou hebben herkend. Onontdekte genieën kunnen hun ideeën dus maar beter naar iemand anders sturen.

Een ouderwetse fietslamp heeft een interessante vorm: als je een dwarsdoorsnede neemt, zie je een parabool. Datzelfde geldt voor schotelantennes, al zijn die iets platter. Waarom hebben deze objecten nou juist een parabool als dwarsdoorsnede, en niet een andere boog of gewoon een stukje van een cirkel? En wat is een parabool eigenlijk precies?

Het leuke is dat er drie verschillende manieren zijn om te beschrijven wat een parabool is. Deze drie manieren betekenen alle drie hetzelfde, maar dat is niet direct te zien.

De eerste is misschien de bekendste, of in ieder geval zoals ik het zelf op school geleerd heb: een parabool is de grafiek die je krijgt bij een kwadratische functie als y = x² of y = -2x² + 3x - 7. De grafiek ziet eruit als een boog.

De tweede manier klinkt wat ingewikkelder. Stel je hebt een vast punt (het “brandpunt”) en een gegeven lijn op een vel papier. Als je dan alle punten tekent die precies even ver van het brandpunt als van die lijn af liggen, dan krijg je een parabool.

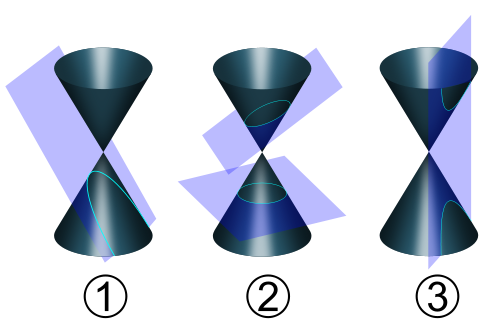
1: parabool, 2: ellips en cirkel, 3: hyperbool

De derde manier vind ik de leukste, omdat je beter ziet wat er gebeurt. Een parabool is één van de zogenaamde kegelsneden, die al door de oude Grieken bestudeerd werden. Als je een dubbele kegel doorsnijdt met vlakken, zoals in het plaatje te zien is, dan krijg je verschillende figuren: een cirkel, ellips, parabool of hyperbool (ook een bepaald soort boog). De parabool is de figuur die je krijgt als grensgeval tussen de ellips en de hyperbool.

Dit kun je zelf zien door een kegelvormige lichtbundel (een zaklamp of spotje bijvoorbeeld) op de muur te laten schijnen. Als je de bundel recht op de muur richt, zie je een cirkel. Als je hem een klein beetje omhoog richt, zie je een ellips. Nog iets verder omhoog gericht is de figuur die je ziet niet meer gesloten, en meer omhoog schijnen levert vanaf dat moment steeds een hyperbool op. Maar op het overgangsmoment tussen de ellips en de hyperbool, het moment dat je de lamp zó houdt dat de zijkant van de lichtkegel precies parallel loopt aan de muur, dan zie je een parabool.

Terug naar de fietslampen en schotelantennes. Hun vorm heet een paraboloïde: de drie-dimensionale figuur die onstaat als een parabool om zijn as gedraaid wordt. Die parabolische vorm heeft een bijzondere eigenschap. Als je zo’n paraboloïde bekleedt met spiegelend materiaal en je zet een lampje in het brandpunt van de parabool, dan wordt het licht zó gereflecteerd dat de lichtstralen die eruitkomen evenwijdig zijn. Dat is fijn bij een fietslamp.

Voor een schotelantenne geldt precies het omgekeerde: wanneer de evenwijdige microgolfstralen op de schotel vallen, worden ze door de schotel zó gereflecteerd dat ze allemaal in het brandpunt uitkomen. De ontvanger wordt in het brandpunt geplaatst, en zo komen alle signalen die door de schotel opgevangen worden netjes in de ontvanger terecht.

De oude Grieken kenden die eigenschap van parabolische spiegels al, al hebben ze er waarschijnlijk nooit een gemaakt, laat staan een schotelantenne.