Dit bericht is geplaatst op zaterdag 5 februari 2011 om 10:00 in categorieën Column. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Hoe maak je dit rijtje af?
In Column, door Jeanine
Deze column verschijnt vandaag in de Volkskrant.

Een tijdje geleden deed ik een “wisquiz” met mijn brugklasleerlingen. Ik stelde onder andere de vraag: wat zijn de drie volgende getallen in het rijtje 1, 4, 9, 16, … ?
Nou kun je strikt gezien bij elke willekeurige drie volgende getallen een wiskundige regel verzinnen die precies die getallen oplevert, maar mijn leerlingen gingen druk op zoek naar een niet al te ingewikkeld patroon, en ze vonden er een. Àlle groepjes noemden als volgende drie getallen 25, 36 en 49. Bij navraag naar het patroon dat ze gevonden hadden, zeiden ze: “Nou, eerst hebben we 1, dan doe je er 3 bij, dan 5, dan 7 en zo verder, dus je doet steeds het volgende oneven getal erbij.” Klopt helemaal.
Maar misschien denkt u verbaasd: “Hè, maar dat zijn toch gewoon de kwadraten?” Klopt ook: 12 = 1, 22 = 4, 32 = 9 en 42 = 16. Dat is grappig. Mijn brugklasleerlingen hadden nog niet geleerd wat een kwadraat is. Wat blijkbaar hun gebruikelijke aanpak is bij zo’n rijtjes-afmaak-som, is kijken naar de verschillen tussen opeenvolgende getallen en of daar een duidelijke regelmaat in zit. En die hadden ze gevonden.
Nou is het op het eerste gezicht best gek dat de regelmaat van mijn leerlingen (steeds het volgende oneven getal erbij optellen) en de regelmaat die mijzelf onmiddellijk in het oog springt (de rij van kwadraten) dezelfde drie volgende getallen opleveren. Dus dan kun je je afvragen: is dat toeval? Of geven deze twee manieren ook bij het vierde, vijfde, zesde, en honderdmiljoenste getal dezelfde antwoorden?
Bij de regel van mijn leerlingen tel je achtereenvolgens bij het getal 1 op: 3, 5, 7, 9, enzovoorts. Het achtste getal in het rijtje is dus de som (optelling) van de eerste acht oneven getallen. Algemeen geformuleerd: het n-de getal in het rijtje is de som van de eerste n oneven getallen, wat voor nummer n ook is. Maar als we het rijtje voortzetten met de kwadratenregel, is het n-de getal in het rijtje het kwadraat van het getal n, oftewel n2.
De vraag is dus: zijn die rijtjes inderdaad hetzelfde, oftewel: is de som van de eerste n oneven getallen gelijk aan n2, voor alle n? Ja, dat is zo, en het is zelfs redelijk eenvoudig om in te zien waarom! Een simpele serie plaatjes laat zien wat er gebeurt.
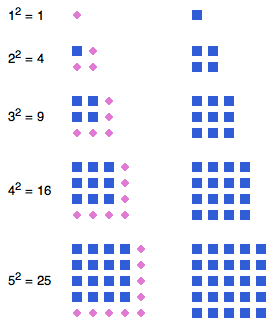
We beginnen met het getal 1: dat ene roze vierkantje linksboven. Vervolgens tellen we daar 3 bij op, in het plaatje daaronder aangegeven door drie roze vierkantjes. Die drie vierkantjes zijn zó neergelegd, dat er precies een vierkant van 2 bij 2 ontstaat, dus je ziet meteen dat daar 22 vierkantjes liggen. En zo gaan we verder. Als er een vierkant ligt van n bij n vierkantjes, dat dus uit n2 vierkantjes bestaat, dan moeten we n + n + 1, oftewel 2n+1 vierkantjes erbij leggen om het volgende kwadraat te leggen. En 2n+1 is precies het volgende oneven getal.
Maakt u zich trouwens vooral geen zorgen: inmiddels weten mijn leerlingen ook wat kwadraten zijn.
 Internetbureau Rotterdam
Internetbureau Rotterdam 
