Internetbureau Rotterdam 
Dit bericht is geplaatst op zaterdag 19 februari 2011 om 09:00 in categorieën Column. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Waar wiskunde goed voor is
In Column, door Ionica
Deze column verschijnt vandaag in De Volkskrant.
Van wiskunde op de middelbare school herinneren veel mensen zich maar twee dingen: de stelling van Pythagoras en de wanhopige vraag waar al die sommen goed voor zijn. Mijn eigen wiskundedocent had helaas nooit een erg bevredigend antwoord op die vraag. En dat terwijl je alleen de stelling van Pythagoras al kunt gebruiken bij het maken van een boomhut of het bestellen van pizza’s.
De eeuwenoude stelling gaat over een rechthoekige driehoek. In zo’n driehoek is het kwadraat van de lengte van de schuine zijde gelijk aan de kwadraten van de lengtes van de twee rechthoekszijden bij elkaar opgeteld. Oftewel: \(\) (waarbij \(\) en \(\) de lengtes van de rechtshoekzijden zijn en \(\) de lengte van de schuine zijde).
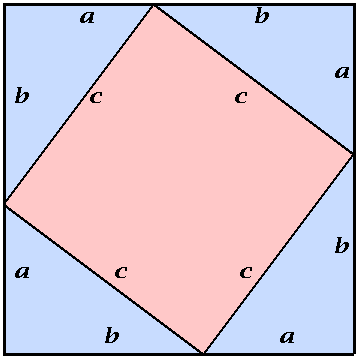
Een plaatjesbewijs voor de stelling van Pythagoras
Op school wordt de stelling vooral gebruikt om de lengte van zijden te bepalen in allerlei driehoeken, parallellogrammen en andere figuren. Maar de stelling van Pythagoras kan ook nuttig zijn bij meer alledaagse problemen, bijvoorbeeld bij het maken van een boomhut (of een hekje, of een schuurtje). Ze helpt je namelijk om zonder geodriehoek of winkelhaak een perfecte rechte hoek te construeren. Je hebt alleen een stukje touw nodig, een mes en iets om mee te meten. Snijd drie stukken touw af van 30, 40 en 50 centimeter en leg deze stukken in een driehoek. De hoek tussen de stukken van 30 en 40 centimeter is nu een rechte hoek, dus daarmee kun je je de wanden van je boomhut keurig haaks op elkaar spijkeren. De driehoek van touw heeft zijden van 30, 40 en 50 centimeter en \(\) (dus \(\)).
Scherpe lezers zullen opmerken dat je eigenlijk niet eens touw nodig hebt voor deze truc. Alleen iets om te te meten is ook al genoeg. Nog scherpere lezers zullen opmerken dat hierbij niet de stelling van Pythagoras wordt gebruikt, maar haar omkering. Als namelijk in een driehoek met zijden \(\) en \(\) geldt dat \(\), dan is het een rechthoekige driehoek. Dat vertellen ze helaas bijna nooit op de middelbare school.
En wat ze al helemaal niet vertellen is dat je de formule \(\) ook kunt gebruiken voor andere vormen dan driehoeken, bijvoorbeeld voor cirkels. Stel dat je in een pizzeria twijfelt: op de kaart staan pizza’s met een diameters van 18, 24 en 30 centimeter. Je bent met een groep en vraagt je af of je beter twee kleine pizza’s kunt nemen of één grootte. Maar dan bedenk je dat \(\). En dat betekent dat de twee pizza’s van 18 en 24 centimeter samen precies even groot zijn als één pizza van 30 centimeter (reken het maar na). Waarschijnlijk ben je een stuk goedkoper uit met één grote pizza. Daar is wiskunde dus goed voor.
zaterdag 19 februari 2011 om 10:59
[...] Dit blogartikel was vermeld op Twitter door Bram van Uden, Kai Bakker. Kai Bakker heeft gezegd: @testtestest Waar wiskunde goed voor is http://dlvr.it/Gzqqc [...]
zondag 20 februari 2011 om 10:30
Een mooi voorbeeld hier is het leggen van (tapijt)tegels. Daarmee moet je natuurlijk midden in de ruimte beginnen omdat wanden nooit helemaal recht worden gebouwd (waarom niet eigenlijk?) Vervolgens gebruik je twaalf tegels om een mooi strak en haaks begin te maken.
zondag 20 februari 2011 om 23:54
Het voorbeeld van de pizza's illustreert niet de toepassing van de stelling van Pythagoras, maar het feit dat je voor het vergelijken van oppervlaktes van cirkels de straal \(\) (of diameter \(\)) moet kwadrateren (oppervlakte = \(\), \(\) resp. \(\) is een constante die je weg kan laten als het om vergelijken gaat). Wat is meer, 3 pizza's met een diameter van 15 cm of 1 pizza met een doorsnede van 26 cm? Die van 26 cm blijkt net iets groter te zijn: \(\), terwijl \(\). Er is nergens een verband met Pythagoras, of een rechthoekige driehoek.
maandag 21 februari 2011 om 12:23
He Sabih Gerez, je hebt mijn ongemakkelijk gevoel bij het pizza verhaal perfect verwoord! Dat toevallig de gebruikte formule de vorm \(\) heeft, maakt het nog niet een toepassing van de Stelling van Pythagoras. Maar misschien kan Ionica nog een nadere toelichting geven ;-)
maandag 21 februari 2011 om 13:30
Het moest een beetje korte door de bocht in de column (want weinig woorden), maar hier staat een uitgebreide (en prachtige) verklaring van het verband
http://betterexplained.com/articles/surprising-uses-of-the-pythagorean-theorem/
dinsdag 22 februari 2011 om 22:17
Hmm, de keuze tussen pizza's van 18 en 24 cm of een van 30 cm hangt natuurlijk ook of je graag een knapperige korst wilt hebben!
Immers bij 18 en 24 cm krijg je 132 cm korst, bij 30 cm slechts 94 cm. Het is maar dat je het weet...
vrijdag 25 februari 2011 om 18:30
Bij een pizza moet ik niet zo snel denken aan de stelling van Pythagoras. Meer aan de inhoud van een cylinder met de straal z en hoogte a ;-)
zondag 27 februari 2011 om 14:37
Wat vertellen jullie de leerlingen als ze vragen waarom ze wiskunde moeten doen? Ik heb 't altijd over logisch leren rederneren, patronen ontdekken, problemen oplossen, netjes en gestructureerd werken, abstract denken en bewijs leveren en dat heb je bij heel veel dingen in het dagelijkse leven nodig...
zaterdag 26 maart 2011 om 01:09
het is 'grote' ipv 'grootte'
vrijdag 19 januari 2018 om 11:53
Ik vind wiskunde niet leuk groetjes nikolai frunza.