Dit bericht is geplaatst op zaterdag 5 maart 2011 om 13:57 in categorieën Column. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Parabolen, fietslampen en schotelantennes
In Column, door Jeanine
Een ouderwetse fietslamp heeft een interessante vorm: als je een dwarsdoorsnede neemt, zie je een parabool. Datzelfde geldt voor schotelantennes, al zijn die iets platter. Waarom hebben deze objecten nou juist een parabool als dwarsdoorsnede, en niet een andere boog of gewoon een stukje van een cirkel? En wat is een parabool eigenlijk precies?
Het leuke is dat er drie verschillende manieren zijn om te beschrijven wat een parabool is. Deze drie manieren betekenen alle drie hetzelfde, maar dat is niet direct te zien.
De eerste is misschien de bekendste, of in ieder geval zoals ik het zelf op school geleerd heb: een parabool is de grafiek die je krijgt bij een kwadratische functie als y = x2 of y = -2x2 + 3x - 7. De grafiek ziet eruit als een boog.
De tweede manier klinkt wat ingewikkelder. Stel je hebt een vast punt (het “brandpunt”) en een gegeven lijn op een vel papier. Als je dan alle punten tekent die precies even ver van het brandpunt als van die lijn af liggen, dan krijg je een parabool.
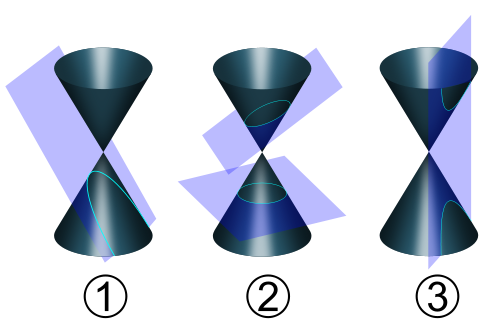
1: parabool, 2: ellips en cirkel, 3: hyperbool
De derde manier vind ik de leukste, omdat je beter ziet wat er gebeurt. Een parabool is één van de zogenaamde kegelsneden, die al door de oude Grieken bestudeerd werden. Als je een dubbele kegel doorsnijdt met vlakken, zoals in het plaatje te zien is, dan krijg je verschillende figuren: een cirkel, ellips, parabool of hyperbool (ook een bepaald soort boog). De parabool is de figuur die je krijgt als grensgeval tussen de ellips en de hyperbool.
Dit kun je zelf zien door een kegelvormige lichtbundel (een zaklamp of spotje bijvoorbeeld) op de muur te laten schijnen. Als je de bundel recht op de muur richt, zie je een cirkel. Als je hem een klein beetje omhoog richt, zie je een ellips. Nog iets verder omhoog gericht is de figuur die je ziet niet meer gesloten, en meer omhoog schijnen levert vanaf dat moment steeds een hyperbool op. Maar op het overgangsmoment tussen de ellips en de hyperbool, het moment dat je de lamp zó houdt dat de zijkant van de lichtkegel precies parallel loopt aan de muur, dan zie je een parabool.
Terug naar de fietslampen en schotelantennes. Hun vorm heet een paraboloïde: de drie-dimensionale figuur die onstaat als een parabool om zijn as gedraaid wordt. Die parabolische vorm heeft een bijzondere eigenschap. Als je zo’n paraboloïde bekleedt met spiegelend materiaal en je zet een lampje in het brandpunt van de parabool, dan wordt het licht zó gereflecteerd dat de lichtstralen die eruitkomen evenwijdig zijn. Dat is fijn bij een fietslamp.
Voor een schotelantenne geldt precies het omgekeerde: wanneer de evenwijdige microgolfstralen op de schotel vallen, worden ze door de schotel zó gereflecteerd dat ze allemaal in het brandpunt uitkomen. De ontvanger wordt in het brandpunt geplaatst, en zo komen alle signalen die door de schotel opgevangen worden netjes in de ontvanger terecht.
De oude Grieken kenden die eigenschap van parabolische spiegels al, al hebben ze er waarschijnlijk nooit een gemaakt, laat staan een schotelantenne.
 Internetbureau Rotterdam
Internetbureau Rotterdam 
