Dit bericht is geplaatst op zaterdag 30 april 2011 om 09:00 in categorieën Column. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Nog eens die drie deuren
In Column, door Ionica
Deze column staat vandaag in de Volkskrant.
Toen ik twee weken geleden over het drie-deuren-probleem schreef, was ik eigenlijk bang dat het verhaal te bekend was en dat de Volkskrant-lezers in koor zouden roepen: “Wisselen natuurlijk!” Voor wie even kwijt is wat het probleem is, een korte herhaling. Een kandidate mag kiezen uit drie deuren, achter één deur staat een auto, achter de twee andere staan geiten. Ze kiest een deur. De presentator, die weet waar de auto staat, opent één van de andere deuren en laat zien dat daar een geit staat. (Merk op dat hij altijd een geit kan tonen, welke deur er ook gekozen is.) Dan biedt hij de kandidate aan dat ze nog mag wisselen naar de andere gesloten deur. Heeft dat zin? Zoals ik hier vorige keer schreef, is het verstandig om te wisselen. De kans dat de auto achter de deur van de eerste keus zit is ⅓ en de kans dat de auto achter de andere dichte deur zit is ⅔.
Veel lezers geloofden hier niets van, ik kreeg een recordaantal emails van lezers die dachten dat beide gesloten deuren een kans van ½ hadden. De krant plaatste een brief waarin zelfs werd beweerd dat de overgebleven deuren elk een kans van ⅔ hadden, wat weer een nieuwe regen van reacties opleverde. En op de twee brieven op de opiniepagina de dag daarna kwam weer een hele reeks mails binnen. Laat ik het daarom nog eens op een andere manier proberen uit te leggen.
Ook al lijken twee dingen hetzelfde, de kansen hoeven niet 50/50 zijn. Een collega van mij demonstreerde dit door me te laten raden wanneer hij jarig is. Ik gokte op 8 oktober en hij antwoordde dat hij op 8 oktober óf 18 augustus jarig is. Wilde ik dan bij mijn eerste gok blijven, of ging ik toch liever voor 18 augustus? In dit geval zal (hopelijk) niemand denken dat de beide data precies dezelfde kans hebben. Zoiets gebeurt ook bij het drie-deuren-probleem.
Eerst nog iets over de verborgen aannames. Elk van de drie deuren heeft aan het begin evenveel kans heeft om de auto te bevatten. Iets subtieler is dat we aannemen dat als de presentator uit twee deuren met geiten kan kiezen, hij er willekeurig één kiest (en bijvoorbeeld niet altijd de dichtstbijzijnde). Onder deze voorwaarden geeft wisselen een twee keer zo grote winkans.
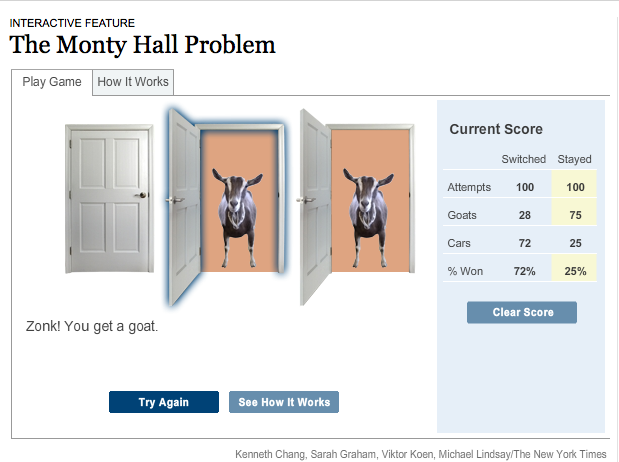
Ik speelde het spel op de site van de New York Times (zie link hieronder) 200 keer: 100 keer met wisselen en 100 keer zonder. Zeer overtuigend resultaat, toch?
Als de kandidate één van de drie deuren kiest, dan heeft ze ⅓ kans op de auto en die kans blijft hetzelfde als ze niet wisselt. Bij wel-wisselen zijn er drie mogelijkheden:
1. Ze kiest geit A, presentator toont geit B, ze wisselt naar de auto.
Ze kiest geit B, presentator toont geit A, ze wisselt naar de auto.
Ze kiest de auto, presentator toont een geit, ze wisselt naar de andere geit.
Ze heeft dus een kans van 2 op 3 om te winnen als ze wisselt.
Wie het nu nog niet gelooft (en ik weet zeker dat er weer mensen tandenknarsend van ergernis achter de krant zitten), kan het eens domweg uitproberen. Verschillende lezers suggereerden om het spel thuis honderd keer na te spelen met een huisgenoot, ondoorzichtige bekers en muntjes. Bij wisselen zul je ongeveer 67 keer winnen, bij niet-wisselen 33 keer. Hoe vaker je speelt, hoe duidelijker de kansverdeling wordt. Voor wie geen huisgenoot (of geduld) heeft: probeer de online-simulatie van de New York Times. Zien is geloven. Eén lezer zag trouwens mogelijkheden om geld te verdienen door tegen overtuigde niet-wisselaars te spelen. Als ik een casino had zou ik dat idee zeker gebruiken.
 Internetbureau Rotterdam
Internetbureau Rotterdam 
