Wiskundemeisjes

Deze column verscheen vandaag in de Volkskrant.

In onze vorige column kon u lezen dat er in Hilberts hotel, een hotel met oneindig veel kamers die genummerd zijn als 1, 2, 3, …, altijd plaats lijkt te zijn. Zelfs als elke kamer bezet is, kan een verdwaalde laatkomer toch een plekje krijgen: iedereen schuift een kamer op. En ook grotere groepen, soms zelfs oneindig groot, pasten er toch steeds weer in.

Dit gaf het gevoel dat alle oneindigheden in Hilberts hotel pasten. Maar wat betekent passen of “even groot” precies? Wiskundigen noemen groepen dingen “even groot” als je ze één op één aan elkaar kunt koppelen. Bijvoorbeeld: er zijn evenveel positieve gehele getallen (1, 2, 3, …) als positieve even getallen (2, 4, 6, …), want je kunt elk getal koppelen aan het dubbele: 1 aan 2, 2 aan 4, 3 aan 6, enzovoorts.

Dit type oneindig heet “aftelbaar”. Er is een duidelijke nummer 1 aan te wijzen, een nummer 2, enzovoorts. Je bent nooit klaar met aftellen, want de verzameling is oneindig, maar je kunt ze op een rijtje zetten, net als 2, 4, 6, … en de kamers in Hilberts hotel. Ook de verzameling van breuken, al lijkt die veel groter, is aftelbaar. Maar niet alle getallen zijn breuken: en zijn beroemde voorbeelden.

De verzameling van alle getallen tussen 0 en 1 is niet aftelbaar. Het bewijs is bijzonder elegant, maar vereist wel enig hersenwerk.

Getallen tussen 0 en 1 hebben een (oneindig lange) decimale ontwikkeling, bijvoorbeeld: of of .

Stel dat je wel een (oneindig lange) lijst kunt opstellen waar ze allemaal op staan. Wat blijkt? Hoe die lijst er ook uitziet, je kunt altijd een nieuw getal tussen 0 en 1 construeren dat niet op de lijst staat. Dat doe je als volgt. We beginnen met 0 en de komma. Nu gaan we de eerste decimaal van het nieuwe getal als volgt bepalen: als de eerste decimaal van het eerste getal op de lijst geen 2 is, kiezen we een 2, en als het wel een 2 was kiezen we een 1.

Nu verschilt de eerste decimaal van ons nieuwe getal van de eerste decimaal van het eerste getal op de lijst. We kiezen op dezelfde manier een tweede decimaal: als de tweede decimaal van het tweede getal op de lijst geen 2 is, kiezen we een 2, anders een 1. Enzovoorts.

Een voorbeeld van een hypothetische lijst met de constructie van een stukje van het nieuwe getal.

Dit nieuwe getal staat nergens op de lijst. Ga maar na: het is niet gelijk aan het eerste getal op de lijst, want de eerste decimaal verschilt. Het is ook niet gelijk aan het 37e getal, want de 37e decimaal verschilt. Kortom: het nieuwe getal ontbreekt op de lijst, wat de lijst ook was! Maar het zou er wel op moeten staan, want het is een getal tussen 0 en 1. Dat betekent dat de getallen tussen 0 en 1 niet op een lijst te zetten zijn, en er dus geen koppeling bestaat met de aftelbare verzameling 1, 2, 3, … . Echt een ander soort oneindig, dus!

Op 24 maart was schrijver John Green in Nederland en mocht ik een lezing geven over de wiskunde in zijn werk. Het programma staat nu online en ik dacht dat jullie het misschien wel leuk zouden vinden om mijn verhaal over Venn-diagrammen, oneindigheden en liefdesformules te zien! Mijn verhaal begint na 22 minuten, maar het interview van Edward van de Vendel met John is zeker ook de moeite waard.

ps Hebben jullie ook Wetenschap 101 al gezien? Dat is de nieuwe videoblog van Govert Schilling en mij.

“Sommige oneindigheden zijn groter dan andere oneindigheden.” Dat is zo’n beetje het motto van John Greens prachtige Een weeffout in onze sterren. In het boek concludeert de 16-jarige Hazel uit deze bewering dat er meer (reële) getallen tussen 0 en 2 liggen dan tussen 0 en 1. Maar die twee oneindigheden zijn juist precies even groot! Green liet dit zijn hoofdpersoon bewust verkeerd doen. Hij vond het een mooi idee dat pubers uit gecompliceerde wiskunde onjuiste conclusies trekken en dan toch iets aan hun eigen redenering hebben.

Oneindig is ook één van de moeilijkste begrippen in de wiskunde. De metafoor van Hilberts Hotel (genoemd naar wiskundige David Hilbert) laat zien hoe raar oneindig zich gedraagt. Hilberts Hotel heeft een oneindig aantal kamers. Die kamers zijn zoals gebruikelijk in een hotel genummerd: 1, 2, 3, enzovoorts. Het hotel is vol, alle kamers zijn bezet. De logische conclusie lijkt dat er geen enkele gast meer bij past.

Dan meldt zich een wanhopige reiziger bij de balie, is er echt geen kamer meer vrij? De receptionist denkt even na en knikt dan enthousiast. Via de intercom vraagt hij alle gasten om één kamer op te schuiven: de gast in kamer 1 gaat naar kamer 2, de gast in kamer 2 naar kamer 3, enzovoorts. Daarna is kamer 1 vrij voor de reiziger en heeft nog steeds elke gast een kamer. Deze oplossing werkt voor elk eindig aantal gasten dat zich meldt aan de balie. Dat is behoorlijk tegenintuïtief: het hotel is vol, maar tegelijkertijd is er altijd plaats voor een willekeurig aantal nieuwe gasten.

En het wordt nog gekker! Een bus van InfinityTravels brengt een (zeer lange) bus met oneindig veel reizigers naar het hotel. Nu zal de receptionist toch zeker moeten zeggen dat er geen plaats is? Maar nee, ook hierop verzint hij een list: hij stuurt alle gasten naar de kamer met het dubbele van hun kamernummer. De gast in kamer 1 gaat naar kamer 2, die in kamer 2 naar kamer 4, die in kamer 3 naar kamer 6, enzovoorts. Dan komen alle kamers met een oneven nummer vrij en kunnen er in een vol hotel dus toch nog oneindig veel gasten bij. (Nu maar hopen dat er ook oneindig veel kamermeisjes zijn.)

Dan komt InfinityTravels na een speciale aanbieding met oneindig veel bussen met daarin elk oneindig veel passagiers. De receptionist kan op dezelfde manier als net oneindig veel kamers leegmaken, maar als hij dan begint met bus 1 in te laden, dan komen de passagiers in de volgende bussen nooit aan de beurt. Maar ook nu verzint de receptionist iets slims: hij begint met passagier 1 van bus 1, daarna mag passagier 1 van bus 2 komen, dan passagier 2 van bus 1 en zo zigzagt hij door alle passagiers in alle bussen en krijgt iedereen een kamer.

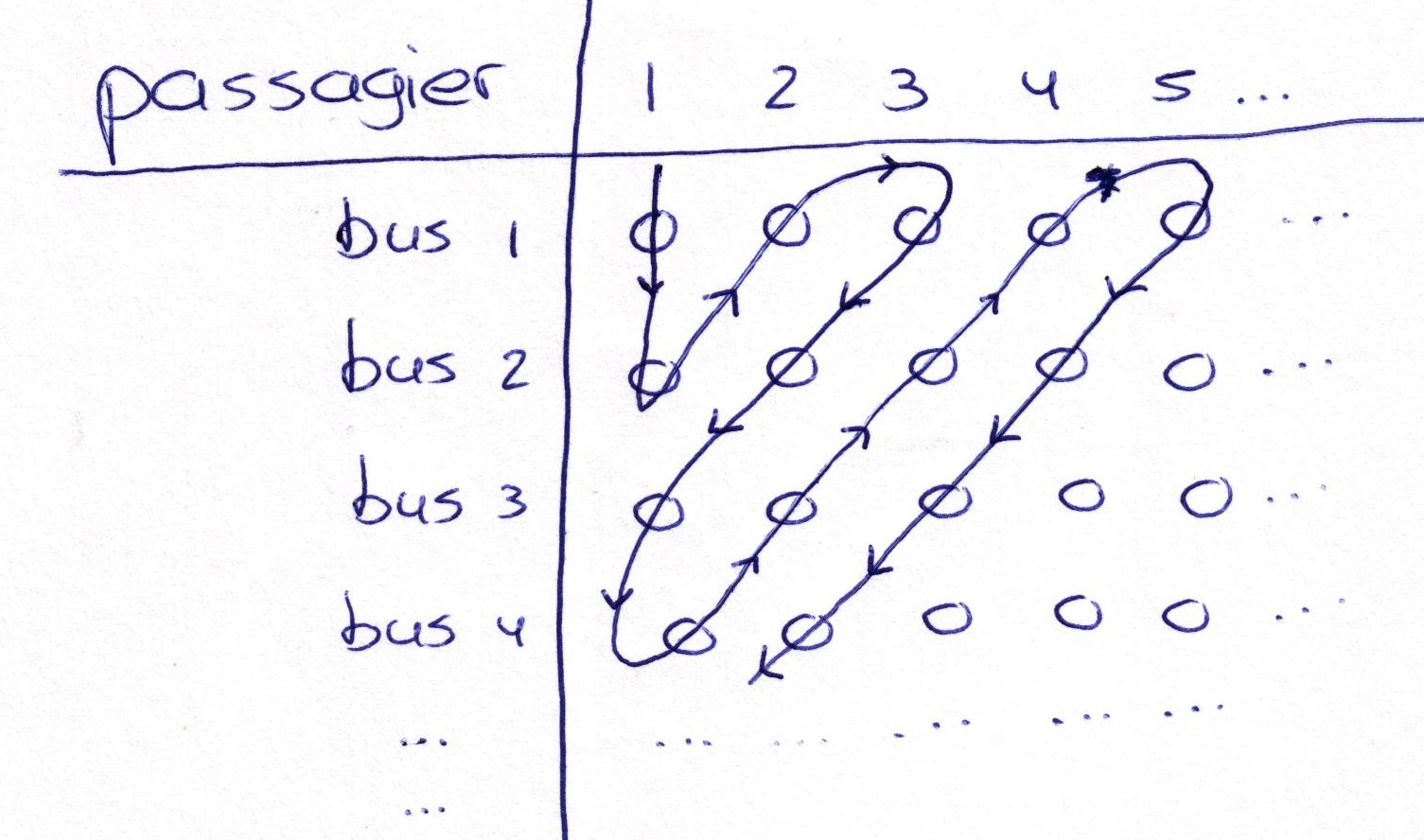
Schema voor het uitladen van de buspassagiers

Het lijkt alsof er altijd plaats is in Hilberts Hotel en toch is er een ander soort oneindig die er níet inpast. Sommige oneindigheden zijn groter dan andere oneindigheden. Maar dat is iets voor een volgende column.

Deze column verscheen gisteren in de Volkskrant.

Genieën spreken tot de verbeelding. En als gewone mensen opeens een onontdekt genie blijken te zijn, spreekt dat nog veel sterker tot de verbeelding. Want wie weet! Misschien hebben wij zelf ook wel een onontdekt groot talent dat ons eeuwige roem en geluk zal brengen! Er is dan ook een niet aflatende stroom aan tv-programma’s te zien die ons, de gewone mensen, uitdagen om onze talenten aan de rest van de wereld te laten zien.

En al is wiskunde misschien niet zo geschikt voor een talentenjacht op televisie, er zijn wel degelijk anekdotes in omloop over onontdekte wiskundegenieën. Een van de bekende urban legends over zo’n wiskundegenie gaat ongeveer als volgt: een gewone student komt een wiskundeprobleem tegen, gaat eraan werken, en lost het op. Zonder te weten dat het betreffende probleem een open, onopgelost wiskundeprobleem was waar de grote geesten hun tanden al op stukgebeten hadden.

Deze verhaallijn zie je terug in de film Good Will Hunting. Een jonge schoonmaker (gespeeld door Matt Damon) maakt de gangen van het MIT schoon en leest zodoende een wiskundevraagstuk op een schoolbord. Hij gaat aan de slag, en jawel: lost het op. Het zogenaamd onopgeloste probleem op het schoolbord in deze film is trouwens in werkelijkheid een standaardopgave die een gemiddelde wiskundestudent makkelijk moet kunnen maken, maar dat is een ander verhaal.

Hoe onwaarschijnlijk de situatie in Good Will Hunting ook is (zonder opleiding is het feitelijk onmogelijk om wiskundenotatie te lezen, hoe slim je ook bent, want dat is gewoon een hele rits afspraken waarvan je weet moet hebben), er zit wel een kern van waarheid in.

In 1939 ging George Dantzig, student in Berkeley, naar een college van professor Jerzy Neyman. Hij was te laat. Toen hij binnenkwam, stonden er twee statistiekproblemen op het bord. Hij nam aan dat het de huiswerkopgaven waren voor deze week, schreef ze over en ging er aan werken. Ze leken wat moeilijker dan anders. Meestal kreeg hij zijn huiswerk wel in een paar uur af, maar nu had hij een paar dagen nodig. Met excuses bracht bij ze naar Neyman, die hem sommeerde het huiswerk maar op zijn bureau te leggen. Een week of zes later bonkte Neyman op zondagochtend opgewonden bij Dantzig op de deur: “Ik heb een inleiding geschreven bij je artikel! Lees het snel even door, dan kan ik het direct opsturen voor publicatie!” Dat was het moment waarop Dantzig merkte dat hij iets bijzonders gedaan had: de problemen die hij opgelost had, bleken open problemen te zijn.

Dantzigs oplossingen werden de basis voor zijn dissertatie. En ook later deed hij belangrijke dingen: hij bedacht de zogenaamde simplexmethode, een methode die veel gebruikt wordt bij optimaliseringsproblemen (denk aan maximaliseren van productie, of het minimaliseren van kosten).

Ik zie deze anekdote persoonlijk liever als een stimulans tot een open blik dan als een verhaal over een onvermoed genie. Dantzig was onbevooroordeeld. Hij wist niet dat het vraagstuk een bekend open probleem was, dus hij benaderde het als ieder ander huiswerkprobleem. Moeilijk, maar ja, het was een huiswerkopgave, dus uiteindelijk zou het moeten lukken. En zo was het.