Dit bericht is geplaatst op zaterdag 14 april 2012 om 11:30 in categorieën Column. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Verwarrende oneindigheden
In Column, door Ionica
“Sommige oneindigheden zijn groter dan andere oneindigheden.” Dat is zo’n beetje het motto van John Greens prachtige Een weeffout in onze sterren. In het boek concludeert de 16-jarige Hazel uit deze bewering dat er meer (reële) getallen tussen 0 en 2 liggen dan tussen 0 en 1. Maar die twee oneindigheden zijn juist precies even groot! Green liet dit zijn hoofdpersoon bewust verkeerd doen. Hij vond het een mooi idee dat pubers uit gecompliceerde wiskunde onjuiste conclusies trekken en dan toch iets aan hun eigen redenering hebben.

Oneindig is ook één van de moeilijkste begrippen in de wiskunde. De metafoor van Hilberts Hotel (genoemd naar wiskundige David Hilbert) laat zien hoe raar oneindig zich gedraagt. Hilberts Hotel heeft een oneindig aantal kamers. Die kamers zijn zoals gebruikelijk in een hotel genummerd: 1, 2, 3, enzovoorts. Het hotel is vol, alle kamers zijn bezet. De logische conclusie lijkt dat er geen enkele gast meer bij past.
Dan meldt zich een wanhopige reiziger bij de balie, is er echt geen kamer meer vrij? De receptionist denkt even na en knikt dan enthousiast. Via de intercom vraagt hij alle gasten om één kamer op te schuiven: de gast in kamer 1 gaat naar kamer 2, de gast in kamer 2 naar kamer 3, enzovoorts. Daarna is kamer 1 vrij voor de reiziger en heeft nog steeds elke gast een kamer. Deze oplossing werkt voor elk eindig aantal gasten dat zich meldt aan de balie. Dat is behoorlijk tegenintuïtief: het hotel is vol, maar tegelijkertijd is er altijd plaats voor een willekeurig aantal nieuwe gasten.
En het wordt nog gekker! Een bus van InfinityTravels brengt een (zeer lange) bus met oneindig veel reizigers naar het hotel. Nu zal de receptionist toch zeker moeten zeggen dat er geen plaats is? Maar nee, ook hierop verzint hij een list: hij stuurt alle gasten naar de kamer met het dubbele van hun kamernummer. De gast in kamer 1 gaat naar kamer 2, die in kamer 2 naar kamer 4, die in kamer 3 naar kamer 6, enzovoorts. Dan komen alle kamers met een oneven nummer vrij en kunnen er in een vol hotel dus toch nog oneindig veel gasten bij. (Nu maar hopen dat er ook oneindig veel kamermeisjes zijn.)
Dan komt InfinityTravels na een speciale aanbieding met oneindig veel bussen met daarin elk oneindig veel passagiers. De receptionist kan op dezelfde manier als net oneindig veel kamers leegmaken, maar als hij dan begint met bus 1 in te laden, dan komen de passagiers in de volgende bussen nooit aan de beurt. Maar ook nu verzint de receptionist iets slims: hij begint met passagier 1 van bus 1, daarna mag passagier 1 van bus 2 komen, dan passagier 2 van bus 1 en zo zigzagt hij door alle passagiers in alle bussen en krijgt iedereen een kamer.
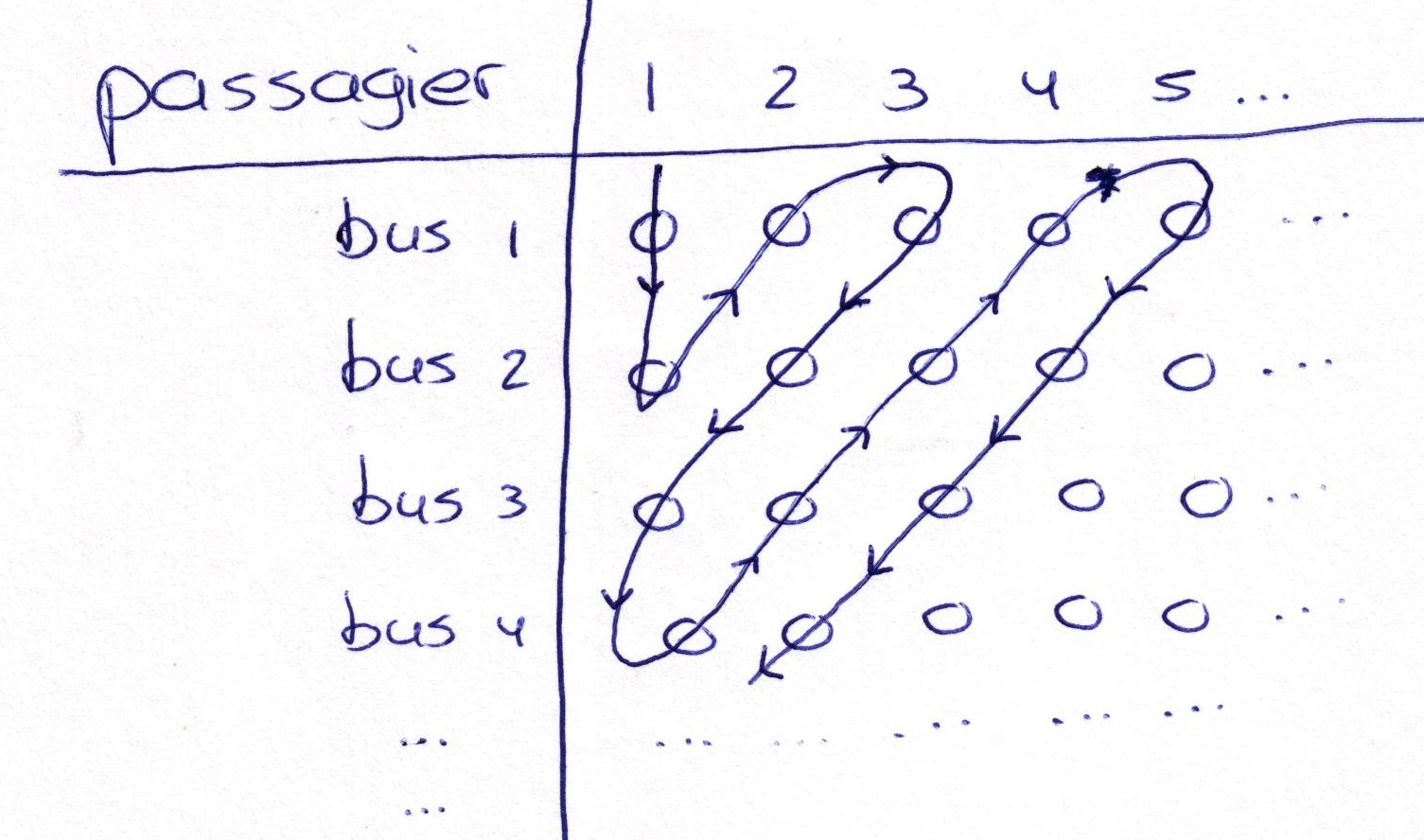
Schema voor het uitladen van de buspassagiers
Het lijkt alsof er altijd plaats is in Hilberts Hotel en toch is er een ander soort oneindig die er níet inpast. Sommige oneindigheden zijn groter dan andere oneindigheden. Maar dat is iets voor een volgende column.
 Internetbureau Rotterdam
Internetbureau Rotterdam 
