webhost van wiskundemeisjes.nl 
Dit bericht is geplaatst op zondag 9 september 2012 om 20:09 in categorieën Column. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Geachte Dr. Jasper Verguts... over de gulden snede
In Column, door Jeanine
Deze column verscheen gisteren in de Volkskrant.
Geachte Dr. Jasper Verguts,
Als gynaecoloog ziet u natuurlijk heel wat baarmoeders. Ik las in The Guardian dat u op het idee bent gekomen om tijdens echo’s die baarmoeders te meten. U mat 5000 baarmoeders op en toen ontdekte u iets opvallends: in de vruchtbaarste periode van een vrouwenleven ligt de verhouding tussen hoogte en breedte van de baarmoeder rond de 1,6. En toen dacht u natuurlijk aan de gulden snede, de beroemde verhouding die alles mooi en goed maakt. U concludeerde dat de gulden-snedeverhouding blijkbaar ook de optimaalste baarmoederverhouding is.
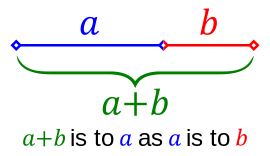
U weet natuurlijk wel wat die beroemde gulden snede precies is. Als je een strook papier in twee stukken verdeelt met lengtes a en b (waarbij a het langste is), en de verhouding a staat tot b (dus het langste ten opzichte van het kortste) gelijk is aan de verhouding a + b staat tot a (dus de hele strook ten opzichte van het langste stuk), dan is die verhouding gelijk aan \(\frac{1+\sqrt{5}}{2}\), ongeveer 1,618.
Binnen de wiskunde duikt dit getal inderdaad op onverwachte plekken op, bijvoorbeeld in de lengteverhoudingen in een pentagram, en ook in de beroemde getallenrij van Fibonacci. Die begint als 1, 1, 2, 3, 5, 8, 13, …, en je krijgt het volgende getal steeds door de twee voorgaande getallen bij elkaar op te tellen. De verhouding tussen een getal en zijn voorganger kruipt, naarmate de getallen verder in de rij staan, steeds dichter naar de gulden snede toe. Dat is wiskundig te bewijzen.
Maar u signaleert de verhouding nu in de baarmoeder. Net zoals die door vele anderen gezocht is in vingerkootjes, muziek van Bach, het Parthenon, piramides, noem maar op. Er wordt vaak beweerd dat de gulden snede een verhouding is die mensen prettig vinden. Daar is echter geen bewijs voor. En als esthetisch principe is de gulden snede pas in de negentiende eeuw gesignaleerd, dus in oude kunst en gebouwen zal hij niet moedwillig gebruikt zijn.
Wat nog vervelender is: door alleen een meting kun je nooit bewijzen dat iets precies de gulden snede is. Zelfs als je heel precies 1,618 gemeten hebt, klopt het een paar decimalen verder niet meer helemaal, en uw 1,6 is maar op één decimaal nauwkeurig. Maar dat is eigenlijk niet eens belangrijk.
Als u goed rondkijkt, ziet u dat veel dingen om ons heen niet extreem lang of smal zijn, wat als gevolg heeft dat de verhoudingen die we zien vaak tussen de 1 en de 2 zullen liggen. Iets in de buurt van de 1,6 is dus niet raar. Net als 1,8 of 1,25. Je kunt bij elke verhouding dingen vinden die er in de buurt zitten, als je er maar naar zoekt.
De baarmoederverhouding waar het om draait is in het begin van het leven ongeveer gelijk aan 2, en bij oude vrouwen 1,46. Qua orde van grootte zitten we dus sowieso al in de buurt. En als iets van 2 verandert in 1,46, ja, dan ligt daartussenin natuurlijk wel een keer ongeveer 1,6, dat is nogal wiedes! Uw verband met de gulden snede lijkt mij nogal vergezocht.
Met hartelijke groeten,
Jeanine
zondag 9 september 2012 om 21:45
In Michael Schneider: Ontdek en creëer zelf het Universum, lees ik:... De Griekse beeldhouwer Phidias die de gulden snede gebruikte om zijn ontwerpen teproportioneren, van het Parthenon tot zijn beroemde beeld van Zeus.
Even verder: Deze verhouding werd bewust in de beeldhouwwerken van de Oudheid gebruikt voor het weergeven van het ideale lichaam van de onsterfelijke goden.Menselijke lichamen werden met opzet minder dan perfect weergegeven.
dinsdag 11 september 2012 om 00:00
Ik heb enkele vragen bij uw column:
Begint de reeks van Fibonacci niet met een NUL?
Het lijkt een verhaal tussen verschillende geloven, maar als die verhouding op de meest vruchtbare leeftijd 1.618 is, dan klopt toch wat hij zegt? Waarom zien we die verhouding dan niet op andere leeftijden?
Als een verhouding alle getallen tussen 2 en 1.46 doorloopt, zal die toch ooit eens exact de gulden snede hebben?
dinsdag 11 september 2012 om 10:57
Ook Devlin en Simanek schreven/spraken er smakelijk over in "Fibonacci Flim-Flam" (http://www.lhup.edu/~dsimanek/pseudo/fibonacc.htm) en "The Myth That Will Not Go Away" (http://www.maa.org/devlin/devlin_05_07.html)
vrijdag 7 december 2012 om 11:44
De uiteindelijke keuze uit het gemiddelde van de getallenreeks van Fibonacci is 2584:1597= 1.6180338134..... hetzelfde probleem met het getal Pi 3.1415955...... Had Fibonnaci gestopt bij het delen van zijn getallen in de getallenreeks namelijk 13:8=1.625 dan zou de gulden snede vandaag 1.625 zijn en dat is de zuivere gulden snede en daar draait de hele natuur rond en ook (zonder dat ik hetzelf heb opgemeten) de baarmoeder. Dus, 1.625. Want 28627:17691=1.61816742976..... zo kunnen we nog uren doorgaan, de hoogste tijd om te herbronnen!
woensdag 6 februari 2013 om 21:02
Meneer Fernand Neerman, Fibonacci heeft niet als enige en zeker niet als eerste die verhouding gevonden. Hij wist zelf al helemaal niets van de gulden snede, maar loste hiermee een vraag over het aantal konijnenparen na x aantal maanden op. Dus dan zou vandaag de dag nog steeds het getal 1,618etc de gulden snede zijn
vrijdag 22 februari 2013 om 17:13
Beste Fernand Neerman, het quotient van twee opeenvolgende termen uit de Fibonacci-reeks benadert, naarmate men verder in de reeks komt, steeds beter de gulden snede met waarde [sqrt(5)+1]/2 = 1.6180339887...
Je eerste twee voorbeelden laten dat ook zien:
13:8=1.625,
2584:1597= 1.6180338134...,
maar je derde voorbeeld is fout, want 28627 en 17691 komen niet in de reeks voor. Goed was geweest:
28657:17711 = 1.6180339901...,
dus nog weer dichter bij de uiteindelijke waarde.
Er is dan ook helemaal geen sprake van een of andere "uiteindelijke keuze uit het gemiddelde van de getallenreeks van Fibonacci", maar van een goed bepaalde limiet.