Dit bericht is geplaatst op maandag 15 oktober 2012 om 09:59 in categorieën Column. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Beste Britse parlementsleden...over kansen en zelfkennis
In Column, door Ionica
Deze column verscheen afgelopen weekend in de Volkskrant.
Beste Britse parlementsleden,
U heeft het natuurlijk niet makkelijk. Een paar jaar geleden kwam naar buiten dat een aantal van uw collega’s nogal gerommeld had met declaraties. Een schandaal. schorsingen, boetes en zelfs gevangenisstraffen volgden. En nu heeft u alweer gedonder met getallen. Vorige week verschenen de resultaten van de jaarlijkse winter-enquete waarvoor meer dan honderd van u persoonlijk zijn geïnterviewd.
Dit jaar was één van de vragen of u zich in het algemeen zeker voelt als u met getallen werkt . Daarop antwoordde maar liefst 77 procent van u bevestigend. Daarna volgde een algemenere vraag: “Gebruiken politici statistiek op de juiste manier als ze over hun beleid praten?”. Dat geloofde nog maar 28 procent van u. U ziet blijkbaar dat uw collega’s er een rommeltje van maken als ze iets met cijfers moeten doen. Maar het kan nog erger, want slechts 15 procent van u denkt dat kranten en televisieprogramma’s statistiek op een juiste manier weergeven. Samengevat: u bent zelf goed met getallen, uw collega’s wat minder en die journalisten begrijpen er al helemaal niets van. Helder.
Het is alleen een beetje jammer dat diezelfde enquete ook een kleine vraag stelde om te testen hoe goed u nu echt bent met cijfers. Om precies te zijn: “Als je twee keer achter elkaar een munt opgooit, wat is dan de kans dat allebei de worpen kop zijn?” Er zijn verschillende manieren om het goede antwoord te beredeneren. De kans dat bij één keer gooien kop boven komt is domweg één op twee. Voor de tweede worp geldt hetzelfde. Die kansen met elkaar vermenigvuldigen geeft het juiste antwoord: de gevraagde kans is één op vier.
Als u even vergeten was hoe het zat met kansen vermenigvuldigen, dan is er nog een andere manier om erover na te denken. Er zijn in totaal vier uitkomsten mogelijk: eerst munt en dan kop, twee keer munt, eerst kop en dan munt en tenslotte twee keer kop. Elk van die uitkomsten is even waarschijnlijk en moet dus een kans van één op vier hebben.
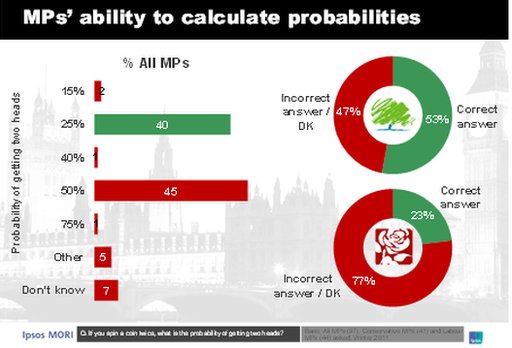
Hé kijk! Groen-rode donuts. Mooi!
Slechts veertig procent van u gaf het juiste antwoord op deze vraag, maar ik vermoed dat dit percentage u niet zoveel zag zeggen. Uw meest gegeven antwoord was namelijk dat de gevraagde kans één op twee is. Dat is kansrekenen van de naïefste soort: Iets gebeurt of het gebeurt niet en die kansen zullen allebei wel even groot zijn. Op die manier is de kans dat u morgenochtend stikt in uw sandwich ook één op twee. Net als de kans dat heel Europa morgen links gaat rijden.
U zult voor deze fout niet in de gevangenis komen en u krijgt ook geen boete. Maar het zou u sieren als degenen die struikelden over deze basissom op zijn minst beseffen dat ze toch niet zo heel goed zijn met cijfers. En als u beleid moet bepalen op basis van percentages, zorg dan dat iemand ze even heel duidelijk komt uitleggen. Sommige journalisten zijn daar best goed in.
Met teleurgestelde groet,
Ionica
 Internetbureau Rotterdam
Internetbureau Rotterdam 
