Dit bericht is geplaatst op maandag 25 maart 2013 om 06:52 in categorieën Column. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Beste Johan Derksen...over eerlijk spelen
In Column, door Ionica
Deze column verscheen afgelopen weekend in de Volkskrant. Helaas zat in die column een fout, hieronder de gecorrigeerde versie.
Beste Johan Derksen,
Vorige week was natuurlijk een rare week voor u. Eerst liep u boos weg bij Voetbal International omdat uw collega Wilfred Genee weer eens iets stom zei. Maar de avond daarna zat u toch weer bij hem aan tafel, omdat u vastzit aan uw contract (en omdat u het natuurlijk heel erg leuk vindt om over voetbal te kletsen). U besprak toen de loting van de Champions League. Eerder die dag waren deze kwartfinales geloot: Malaga-Dortmund, Madrid-Galatasaray, PSG-Barcelona en Bayern-Juventus. Uw collega René van der Gijp vatte het als volgt samen: “Dit kan toch bijna niet waar zijn. De Spanjaarden ontlopen elkaar en de Duitsers ontlopen elkaar.” U voegde daar even later aan toe: “Dit riekt naar malversatie. Het is duidelijk dat Bayern en Barcelona verder moeten.”
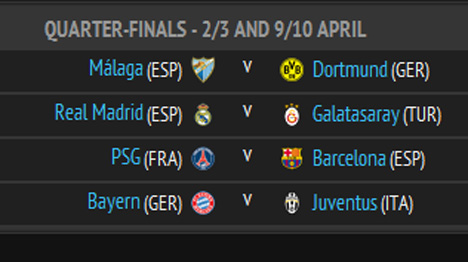
De loting.
Er zijn verschillende dingen opmerkelijk aan deze loting: “de grote vier” (Madrid, Barcelona, Bayern en Dortmund) ontwijken elkaar en het derde Spaanse team Malaga speelt niet tegen andere Spanjaarden. Dat komt wel heel mooi uit voor een organisatie die zoveel mogelijk kijkers wil trekken. Zelfs Wilfred Genee had door dat dit merkwaardig was en noemde het oplichterij van de eerste orde. U mompelde instemmend: “Je kunt het nooit hardmaken, maar dit is te mooi voor woorden.”
Hardmaken is lastig, maar u kunt wel uitrekenen wat de kans op zo’n loting is. Voetballiefhebber en wiskundige Henk Tijms ging aan de slag (en tipte mij over dit onderwerp). De kans dat het eerste team van de grote vier geen van de andere drie treft is \(\). Voor het tweede team is die kans dan \(\) en voor het derde team \(\). Het vierde team zit dan automatisch goed. De totale kans op een loting waarbij de vier teams elkaar ontwijken is daarmee \(\). Nemen we ook nog de kans mee dat Malaga niet tegen een Spaans team uitkomt, dan is de kans op zo’n loting vier op vijfendertig, oftewel ruim elf procent. Dat is niet extreem klein. Zo’n loting is waarschijnlijker dan een tatoeage van Wilfred Genee omringd door hartjes op uw bovenarm.
Nu weet u dus wat de kans is dat de gegeven uitslag valt als de loting eerlijk was. Maar eigenlijk wilt u weten wat de kans is dat deze loting eerlijk is áls deze uitslag valt. Dat is een stuk lastiger. Om dat te berekenen moet u eigenlijk vóór de loting zeggen hoe groot u de kans acht dat er gesjoemeld wordt om te zorgen dat de wedstrijden precies zo uitkomen als hierboven. Na de uitslag kunt u dan de kans uitrekenen dat de loting eerlijk was. Zeg dat u voor de loting inschatte dat er vijfentwintig procent kans was op valsspelen. In dat geval stijgt met de gegeven lotingsuitslag de kans op doorgestoken kaart naar bijna vijfenzeventig procent- volgens u en de wiskunde. De complete berekening past helaas niet in deze brief, maar op deze manier kunt u misschien wel degelijk hardmaken dat de loting te mooi voor woorden is.
Dat de beste moge winnen,
Ionica
 Internetbureau Rotterdam
Internetbureau Rotterdam 
