Wiskundemeisjes

Een ouderwetse fietslamp heeft een interessante vorm: als je een dwarsdoorsnede neemt, zie je een parabool. Datzelfde geldt voor schotelantennes, al zijn die iets platter. Waarom hebben deze objecten nou juist een parabool als dwarsdoorsnede, en niet een andere boog of gewoon een stukje van een cirkel? En wat is een parabool eigenlijk precies?

Het leuke is dat er drie verschillende manieren zijn om te beschrijven wat een parabool is. Deze drie manieren betekenen alle drie hetzelfde, maar dat is niet direct te zien.

De eerste is misschien de bekendste, of in ieder geval zoals ik het zelf op school geleerd heb: een parabool is de grafiek die je krijgt bij een kwadratische functie als y = x² of y = -2x² + 3x - 7. De grafiek ziet eruit als een boog.

De tweede manier klinkt wat ingewikkelder. Stel je hebt een vast punt (het “brandpunt”) en een gegeven lijn op een vel papier. Als je dan alle punten tekent die precies even ver van het brandpunt als van die lijn af liggen, dan krijg je een parabool.

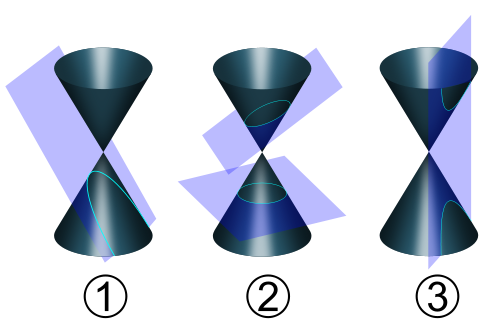
1: parabool, 2: ellips en cirkel, 3: hyperbool

De derde manier vind ik de leukste, omdat je beter ziet wat er gebeurt. Een parabool is één van de zogenaamde kegelsneden, die al door de oude Grieken bestudeerd werden. Als je een dubbele kegel doorsnijdt met vlakken, zoals in het plaatje te zien is, dan krijg je verschillende figuren: een cirkel, ellips, parabool of hyperbool (ook een bepaald soort boog). De parabool is de figuur die je krijgt als grensgeval tussen de ellips en de hyperbool.

Dit kun je zelf zien door een kegelvormige lichtbundel (een zaklamp of spotje bijvoorbeeld) op de muur te laten schijnen. Als je de bundel recht op de muur richt, zie je een cirkel. Als je hem een klein beetje omhoog richt, zie je een ellips. Nog iets verder omhoog gericht is de figuur die je ziet niet meer gesloten, en meer omhoog schijnen levert vanaf dat moment steeds een hyperbool op. Maar op het overgangsmoment tussen de ellips en de hyperbool, het moment dat je de lamp zó houdt dat de zijkant van de lichtkegel precies parallel loopt aan de muur, dan zie je een parabool.

Terug naar de fietslampen en schotelantennes. Hun vorm heet een paraboloïde: de drie-dimensionale figuur die onstaat als een parabool om zijn as gedraaid wordt. Die parabolische vorm heeft een bijzondere eigenschap. Als je zo’n paraboloïde bekleedt met spiegelend materiaal en je zet een lampje in het brandpunt van de parabool, dan wordt het licht zó gereflecteerd dat de lichtstralen die eruitkomen evenwijdig zijn. Dat is fijn bij een fietslamp.

Voor een schotelantenne geldt precies het omgekeerde: wanneer de evenwijdige microgolfstralen op de schotel vallen, worden ze door de schotel zó gereflecteerd dat ze allemaal in het brandpunt uitkomen. De ontvanger wordt in het brandpunt geplaatst, en zo komen alle signalen die door de schotel opgevangen worden netjes in de ontvanger terecht.

De oude Grieken kenden die eigenschap van parabolische spiegels al, al hebben ze er waarschijnlijk nooit een gemaakt, laat staan een schotelantenne.

Deze column verschijnt vandaag in De Volkskrant.

Van wiskunde op de middelbare school herinneren veel mensen zich maar twee dingen: de stelling van Pythagoras en de wanhopige vraag waar al die sommen goed voor zijn. Mijn eigen wiskundedocent had helaas nooit een erg bevredigend antwoord op die vraag. En dat terwijl je alleen de stelling van Pythagoras al kunt gebruiken bij het maken van een boomhut of het bestellen van pizza’s.

De eeuwenoude stelling gaat over een rechthoekige driehoek. In zo’n driehoek is het kwadraat van de lengte van de schuine zijde gelijk aan de kwadraten van de lengtes van de twee rechthoekszijden bij elkaar opgeteld. Oftewel: (waarbij en de lengtes van de rechtshoekzijden zijn en de lengte van de schuine zijde).

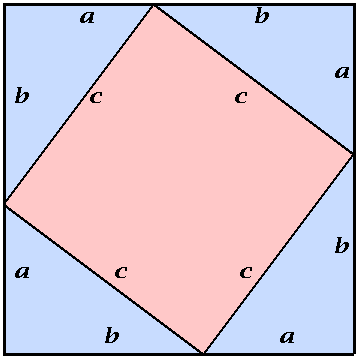
Een plaatjesbewijs voor de stelling van Pythagoras

Op school wordt de stelling vooral gebruikt om de lengte van zijden te bepalen in allerlei driehoeken, parallellogrammen en andere figuren. Maar de stelling van Pythagoras kan ook nuttig zijn bij meer alledaagse problemen, bijvoorbeeld bij het maken van een boomhut (of een hekje, of een schuurtje). Ze helpt je namelijk om zonder geodriehoek of winkelhaak een perfecte rechte hoek te construeren. Je hebt alleen een stukje touw nodig, een mes en iets om mee te meten. Snijd drie stukken touw af van 30, 40 en 50 centimeter en leg deze stukken in een driehoek. De hoek tussen de stukken van 30 en 40 centimeter is nu een rechte hoek, dus daarmee kun je je de wanden van je boomhut keurig haaks op elkaar spijkeren. De driehoek van touw heeft zijden van 30, 40 en 50 centimeter en (dus ).

Scherpe lezers zullen opmerken dat je eigenlijk niet eens touw nodig hebt voor deze truc. Alleen iets om te te meten is ook al genoeg. Nog scherpere lezers zullen opmerken dat hierbij niet de stelling van Pythagoras wordt gebruikt, maar haar omkering. Als namelijk in een driehoek met zijden en geldt dat , dan is het een rechthoekige driehoek. Dat vertellen ze helaas bijna nooit op de middelbare school.

En wat ze al helemaal niet vertellen is dat je de formule ook kunt gebruiken voor andere vormen dan driehoeken, bijvoorbeeld voor cirkels. Stel dat je in een pizzeria twijfelt: op de kaart staan pizza’s met een diameters van 18, 24 en 30 centimeter. Je bent met een groep en vraagt je af of je beter twee kleine pizza’s kunt nemen of één grootte. Maar dan bedenk je dat . En dat betekent dat de twee pizza’s van 18 en 24 centimeter samen precies even groot zijn als één pizza van 30 centimeter (reken het maar na). Waarschijnlijk ben je een stuk goedkoper uit met één grote pizza. Daar is wiskunde dus goed voor.

Deze column verschijnt vandaag in de Volkskrant.

Een tijdje geleden deed ik een “wisquiz” met mijn brugklasleerlingen. Ik stelde onder andere de vraag: wat zijn de drie volgende getallen in het rijtje 1, 4, 9, 16, … ?

Nou kun je strikt gezien bij elke willekeurige drie volgende getallen een wiskundige regel verzinnen die precies die getallen oplevert, maar mijn leerlingen gingen druk op zoek naar een niet al te ingewikkeld patroon, en ze vonden er een. Àlle groepjes noemden als volgende drie getallen 25, 36 en 49. Bij navraag naar het patroon dat ze gevonden hadden, zeiden ze: “Nou, eerst hebben we 1, dan doe je er 3 bij, dan 5, dan 7 en zo verder, dus je doet steeds het volgende oneven getal erbij.” Klopt helemaal.

Maar misschien denkt u verbaasd: “Hè, maar dat zijn toch gewoon de kwadraten?” Klopt ook: 1² = 1, 2² = 4, 3² = 9 en 4² = 16. Dat is grappig. Mijn brugklasleerlingen hadden nog niet geleerd wat een kwadraat is. Wat blijkbaar hun gebruikelijke aanpak is bij zo’n rijtjes-afmaak-som, is kijken naar de verschillen tussen opeenvolgende getallen en of daar een duidelijke regelmaat in zit. En die hadden ze gevonden.

Nou is het op het eerste gezicht best gek dat de regelmaat van mijn leerlingen (steeds het volgende oneven getal erbij optellen) en de regelmaat die mijzelf onmiddellijk in het oog springt (de rij van kwadraten) dezelfde drie volgende getallen opleveren. Dus dan kun je je afvragen: is dat toeval? Of geven deze twee manieren ook bij het vierde, vijfde, zesde, en honderdmiljoenste getal dezelfde antwoorden?

Bij de regel van mijn leerlingen tel je achtereenvolgens bij het getal 1 op: 3, 5, 7, 9, enzovoorts. Het achtste getal in het rijtje is dus de som (optelling) van de eerste acht oneven getallen. Algemeen geformuleerd: het n-de getal in het rijtje is de som van de eerste n oneven getallen, wat voor nummer n ook is. Maar als we het rijtje voortzetten met de kwadratenregel, is het n-de getal in het rijtje het kwadraat van het getal n, oftewel n².

De vraag is dus: zijn die rijtjes inderdaad hetzelfde, oftewel: is de som van de eerste n oneven getallen gelijk aan n², voor alle n? Ja, dat is zo, en het is zelfs redelijk eenvoudig om in te zien waarom! Een simpele serie plaatjes laat zien wat er gebeurt.

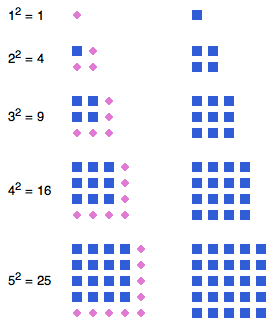
We beginnen met het getal 1: dat ene roze vierkantje linksboven. Vervolgens tellen we daar 3 bij op, in het plaatje daaronder aangegeven door drie roze vierkantjes. Die drie vierkantjes zijn zó neergelegd, dat er precies een vierkant van 2 bij 2 ontstaat, dus je ziet meteen dat daar 2² vierkantjes liggen. En zo gaan we verder. Als er een vierkant ligt van n bij n vierkantjes, dat dus uit n² vierkantjes bestaat, dan moeten we n + n + 1, oftewel 2n+1 vierkantjes erbij leggen om het volgende kwadraat te leggen. En 2n+1 is precies het volgende oneven getal.

Maakt u zich trouwens vooral geen zorgen: inmiddels weten mijn leerlingen ook wat kwadraten zijn.

Deze column verschijnt vandaag in de Volkskrant.

Vorige week moest ik weer eens heel lang wachten op tram 9. (Het begin van deze column is trouwens gelogen. Ik ben sinds kort moeder en het lukt me nauwelijks om een rondje door Leiden te lopen. Laat staan dat ik de trein naar Amsterdam neem om daar een beetje op tram 9 te wachten. Maar ik geef deze columns graag een schijn van actualiteit, daarom schrijf ik “vorige week” in plaats van “een paar maanden geleden”.) Toen eindelijk de juiste tram de hoek omkwam, zag ik dat erachteraan gelijk nóg een tram 9 kwam. Was dit na de OV-chipkaart een nieuwe manier om reizigers te pesten? Een dienstregeling met na een lange tussenpoos steeds twee trams achter elkaar? Of voelden de tramchauffeurs zich niet meer veilig na alle PVV-retorica en durfden ze alleen samen op pad?

In de tram bedacht ik echter dat het onvermijdelijk is dat trams regelmatig op deze manier samenklonteren. Stel dat de trams normaal tien minuten na elkaar rijden. Als een tram op de een of andere manier vertraging oploopt (met toeristen die moeizaam vragen of deze tram naar de Dam rijdt, een fietser die in de rails klemzit of een verhuisbusje dat op de trambaan wordt uitgeladen), dan verzamelen zich bij zijn volgende haltes iets meer passagiers. De tram komt daar immers wat later en dus hebben mensen langer de tijd om aan te komen bij de halte. Vervolgens duurt het instappen wat langer, waardoor de tram nog meer vertraging oploopt. Waardoor bij de volgende haltes weer meer mensen zullen staan te wachten. Waardoor het instappen nóg langer duurt, enzovoorts. Het is een proces dat zichzelf versterkt. De eerste tram na de vertraagde tram heeft het extra makkelijk, want daarop staan juist minder passagiers te wachten. Deze tram zal dus juist een beetje inlopen op zijn schema. En op een gegeven moment zullen de twee trams pal achter elkaar rijden. 

Het grappige is dat passagiers het verschijnsel alleen maar erger maken. Let maar eens op, bij twee trams die achter elkaar rijden, probeert iedereen in de voorste te stappen. Meestal staat het complete gangpad daar bomvol, terwijl de tweede tram vrijwel leeg is. 

Er is ook weinig aan te doen: meer trams inzetten helpt niet. Een dienstregeling waarbij de tram af en toe een paar minuten bij een halte wacht helpt wel. Dan heeft de tram een buffer en kan hij die paar minuten wachten overslaan als hij vertraging heeft opgelopen. Maar zo’n dienstregeling is waarschijnlijk irritanter voor passagiers dan af en toe een duo-tram.

Bussen hebben last van hetzelfde verschijnsel, maar bij treinen zie je er bijna nooit twee pal na elkaar rijden. Misschien doordat er meer tijd voor het instappen is ingepland, of doordat er minder haltes zijn, of doordat de dienstregeling bij een beetje vertraging als snel compleet in de soep loopt. Gelukkig heb ik dáár ook weinig last van tijdens mijn zwangerschapsverlof.

Deze column verschijnt vandaag in de Volkskrant.

In de weersverwachting van de komende vijf dagen staat altijd per dag een neerslagkans, keurig als een percentage. “Zaterdag 60% kans op neerslag”, bijvoorbeeld. Kansen worden namelijk in percentages uitgedrukt, of in een getal tussen 0 en 1 (een kans van 25% komt overeen met een kans van 0,25).

Soms is het duidelijk wat een kans betekent. Als je met een eerlijke dobbelsteen gooit, dan zul je na heel vaak gooien in één op de zes gevallen een 4 gegooid hebben. De kans op een 4 is dus 1/6 (ongeveer 17%).

Maar ik heb me wel eens afgevraagd wat die neerslagkansen nou eigenlijk betekenen. Als richtlijn werken ze prima, en dat is natuurlijk waar ze voor zijn. Maar als wiskundige wil ik het graag preciezer weten. Betekent 60% kans op neerslag dat de kans 60% is dat het vandaag ergens in het land gaat regenen of sneeuwen? Dat lijkt me niet. Als er in Zuid-Limburg een wolkbreuk aankomt, maar in de rest van het land schijnt de zon, wil je eigenlijk niet dat de neerslagkans heel hoog is. Ik vermoed dat het betekent dat een willekeurige plek 60% kans op neerslag heeft. Of betekent het dat het in 60% van het land zal gaan regenen? Of dat in ongeveer 60% van de tijd neerslag naar beneden komt? Dat zou ook kunnen.

Wat het weer gaat zijn, is sowieso moeilijk te berekenen. Daar zitten heel ingewikkelde modellen achter, en soms voorspellen verschillende modellen iets anders uit dezelfde gegevens. Wat bedoelt het KNMI dan met zo’n percentage?

Ik ben dus even gaan rondneuzen op de site van het KNMI, waar inderdaad extra uitleg te vinden is. Het weer voorspellen kan nooit met absolute zekerheid, maar soms zijn er dagen waarop de weerkundigen vrijwel zeker weten dat het gaat regenen of juist niet, en op andere dagen is er meer twijfel. Het KNMI schrijft: “Om die mate van onzekerheid aan te geven wordt de kans op neerslag aangegeven in een percentage.” Omdat er altijd enige onzekerheid is, is dat percentage vrijwel nooit 0 of 100.

Wat ook snel duidelijk wordt: de neerslagpercentages gelden voor een willekeurige plaats in Nederland. Als de kans op neerslag 90% is, is het vrijwel zeker dat er op de plek waar ik ben wat naar beneden komt. Als die kans maar 10% is, blijft het vrijwel zeker overal droog. Bij een kans van 50% kan het op een willekeurige plaats net zo goed droog zijn als regenen of sneeuwen, daar zijn de voorspellingen niet duidelijk over. Over hoeveelheden en tijdsduur van de regen zegt het percentage dus niets. Tegenwoordig staat de neerslaghoeveelheid daarom óók vermeld in de verwachtingen.

Op het moment dat ik dit schrijf, voorspelt het KNMI voor de week dat deze krant verschijnt: “70% kans op aanhouden van het kwakkelweer, 30% kans op vrij zacht weer”. Ik hoop dat het het laatste is geworden, want die sneeuw ben ik inmiddels behoorlijk zat. En dat weet ik wèl zeker.

Deze column verschijnt vandaag in de Volkskrant.

Ongetwijfeld wordt deze kerstvakantie A beautiful mind weer eens herhaald op televisie. Deze Oscarwinnende film beschrijft het leven van wiskundige John Nash. Hij deed op jonge leeftijd briljant werk, maar kreeg paranoïde schizofrenie en was tientallen jaren in de ban van waanideeën. Hij herstelde na dertig jaar van zijn ziekte en ontving op 66-jarige leeftijd de Nobelprijs voor Economie voor zijn jeugdwerk. Een prachtig verhaal voor een feel-good-movie natuurlijk. Alleen jammer dat A beautiful mind soms wat weinig lijkt te begrijpen van wiskunde.

Zo probeert de film in een barscène Nash’s belangrijkste idee uit te leggen. Wie de film heeft gezien, herinnert zich het vast: Nash zit met een groepje vrienden in de kroeg en ze zien een groepje vrouwen. Eén vrouw (een blondine) is het mooiste, haar vriendinnen (brunettes) zijn iets minder aantrekkelijk. De vraag is nu wat de beste strategie is voor de vrienden om deze vrouwen te versieren, onder de aanname dat elke man het liefste de blondine wil, maar dat een brunette beter is dan geen vrouw.

De kroegtijgers uit A beautiful mind

De vrienden van Nash willen in eerste instantie allemaal tegelijk op de blondine afgaan om haar te versieren. Maar Nash werpt tegen dat dit een domme strategie is: de blondine zal arrogant worden en hen stuk voor stuk afwijzen. Daarna hebben de brunettes geen zin om tweede keus te zijn, dus uiteindelijk gaat iedereen alleen naar huis. Nash heeft een beter idee. Als nu eens niemand op de blondine afgaat, maar alle mannen gelijk op een brunette afstappen. Dan zijn hun kansen op succes veel groter! En een brunette is immers beter dan niets.

De film probeert hiermee het Nash-evenwicht te illustreren, een begrip uit de speltheorie. Kort door de bocht heb je in speltheorie een aantal spelers die elk een doel hebben (in dit voorbeeld is dat een zo mooi mogelijke vrouw versieren). Elke speler kan kiezen uit verschillende strategieën en weet niet wat de anderen doen. Hij moet met beperkte informatie een zo goed mogelijke strategie kiezen.

Nash bewees dat er (onder bepaalde voorwaarden) een evenwichtssituatie bestaat, waarbij elke speler zijn strategie niet meer kan verbeteren - ook niet als hij wél zou weten wat de anderen doen. Deze situatie wordt het Nash-evenwicht genoemd en dit is precies het werk waarvoor hij zijn Nobelprijs kreeg.

Waar gaat A beautiful mind nu de fout in? Het probleem bij de strategie die Nash in de film voorstelt, is dat het helemaal geen evenwicht is: elke man kan zijn strategie verbeteren door als enige op de blondine af te stappen. Een strategie die wel een Nash-evenwicht is, is bijvoorbeeld dat één man op de blondine afstapt en de anderen op de brunettes. En wie de mooiste vrouw dan krijgt? Dat ligt nogal voor de hand: de aantrekkelijkste man.

Aan het einde van de kroegscène lijkt Nash trouwens sjans te hebben met de blondine. Maar hij rent terug naar zijn kamer omdat hij liever verder wil werken aan zijn wiskunde. Dat hebben de filmmakers dan weer wel goed begrepen van wiskundigen.

Deze column verschijnt vandaag in de Volkskrant.

Ik heb een kleine obsessie voor bepaalde koppen in het wetenschapsnieuws in de krant en (vooral!) op internet. Denk aan koppen als “Drink More Diet Soda, Gain More Weight”, waarin een bepaald verband tussen twee fenomenen wordt genoemd, maar tegelijkertijd de suggestie gewekt wordt dat er een oorzakelijk verband bestaat tussen het een en het ander.

De kop lijkt te zeggen dat het drinken van light-frisdranken ervoor zorgt dat je zwaarder wordt, wat natuurlijk onzin is. Er bestaat wel een correlatie tussen aankomen en light-frisdrank drinken, maar de oorzaak-gevolg-relatie ligt precies andersom: mensen die zwaarder worden, zullen eerder de neiging hebben light-frisdrank te nemen.

Denkfouten als deze liggen op de loer als je het verschil tussen correlatie en causaliteit niet genoeg in acht neemt. Als twee fenomenen vaak samen optreden (correlatie), betekent dat niet per se dat het één het ander veroorzaakt (causaliteit). Deze drogreden heeft een mooie naam: cum hoc ergo propter hoc (Latijn voor: met dit, dus vanwege dit).

Er zijn verschillende andere mogelijkheden: misschien veroorzaakt het ander juist wel het één, zoals in het voorbeeld hierboven. Soms is een correlatie gewoon toeval. En soms zijn er een heleboel onoverzichtelijke andere factoren die invloed hebben, zoals bij correlaties in de complexe wereldeconomie.

Of misschien, en dat vind ik de leukste optie: misschien is er een duidelijke derde factor die de beide fenomenen veroorzaakt. Een klassiek voorbeeld is de correlatie tussen het aantal ingezette brandweerlieden en de schade die een brand veroorzaakt. Veroorzaken veel brandweermannen de grotere schade? Nee, natuurlijk niet. Er worden meer brandweermannen ingezet omdat het een grote brand is, en een grote brand levert meer schade op. Maar in veel gevallen ligt het wat subtieler en zie je niet meteen wat er niet klopt.

Een mooi voorbeeld hoorde ik een tijd geleden in een lezing van voedingswetenschapper Martijn Katan. Hij vertelde over een onderzoek dat uitwijst dat er een correlatie bestaat tussen het risico op dementie en weinig sporten, met als bijbehorende kop: “Sporten doet risico op dementie verminderen”. Maar het zou ook kunnen dat beginnende dementie ervoor zorgt dat je weinig sport. Of er zou een derde factor kunnen zijn, bijvoorbeeld ongezond leven (roken, veel alcohol drinken, vet eten), die vaak samengaat met weinig sporten en bovendien een risicofactor is voor dementie.

Als ik zo’n kop lees, vind ik het leuk er zelf mogelijke derde factoren bij te verzinnen. Gewoon als gedachte-experiment, om eens te kijken hoe waarschijnlijk zo’n verband nou eigenlijk is als je alleen je gezonde verstand gebruikt. Met als bijeffect dat je het artikel kritischer gaat lezen. En vaak blijkt dan tijdens het lezen dat het verband wat subtieler ligt dan de kop suggereert. Soms zal er natuurlijk wèl een oorzakelijk verband zijn, maar daar heb je meer argumenten voor nodig dan het optreden van een correlatie alleen.

Ik denk overigens wel dat er een causaal verband bestaat tussen mijn wiskundige achtergrond en mijn obsessie met deze denkfout. Of zou ook daar een derde factor in het spel zijn? Hmmm.

Deze column verschijnt vandaag in de Volkskrant.

In het vrolijke boek Superslimme dieren laat Jan Paul Schutten zien hoe snugger dieren zijn. De spinkrab verkleedt zich om onzichtbaar op te gaan in zijn omgeving, franjeapen stelen houtskool van de barbecue tegen maagklachten en vuurvliegjes sturen elkaar boodschappen met knipperlichtjes. Maar het mooiste voorbeeld (voor een wiskundige) is hoe mieren de grootte van een nest schatten. De verkenners van de soort eptothorax albipennis zoeken een opening in de rotsen die geschikt is om een nest in te bouwen. Het moet precies groot genoeg zijn voor het aantal mieren in de kolonie. Hoe schatten de verkenners de grootte van het oppervlak? Ze hebben geen meetlatten en kunnen niet veel meer doen dan een beetje rondlopen.

Een voor de hand liggend idee is dat de mieren domweg langs de omtrek van de grot lopen en zo een zeer grove schatting maken van de oppervlakte. Maar toen onderzoekers in een laboratorium twee nesten bouwden met dezelfde omtrek en verschillende oppervlaktes, namen de mieren consequent het grootste nest. Dus de mieren verkozen zeer terecht een nest van 8 bij 10 centimeter boven één van 3 bij 15 centimeter, terwijl beide nesten een omtrek van 36 centimeter hebben.

Onderzoekers dachten toen dat de verkennende mier misschien kris-kras door de ruimte loopt en bijhoudt hoe ver hij kan lopen tot hij tegen een wand of obstakel opbotst. Hoe langer hij gemiddeld kan lopen, hoe groter het nest is. Maar ook dit idee werd afgeschoten in een laboratoriumopstelling toen onderzoekers een dun wandje midden in een nest plaatsten. De mieren kozen dit nest net zo vaak als een even groot nest zonder dat dunne wandje.

Wat doen mieren dan wel? Het lijkt erop dat ze iets gebruiken dat wiskundigen kennen als de naald van Buffon. De graaf van Buffon stelde in de 18de eeuw een vraag over naalden. Stel dat je een vloer van even brede planken hebt en dat je een naald op deze vloer laat vallen: Wat is de kans dat de naald over de lijn tussen twee planken valt? Als de naald even lang is als de planken breed zijn, dan is het antwoord . Dit principe kan worden uitgebreid om de oppervlakte van een vlak te schatten. Strooi twee even grote sets naalden op het vlak en tel hoe vaak een naald van de eerste set een naald uit de tweede verzameling raakt. De oppervlakte van het vlak is dan ongeveer gelijk aan 2 /( * het aantal snijpunten).

Het lijkt erop dat mieren deze truc toepassen door een grillig pad door het nest te lopen (de eerste set naalden) en daarna een tweede wandeling te maken en te tellen hoe vaak ze het geurspoor van hun eerste pad kruisen. Verkenners vertragen tenminste steeds even als ze hun eerdere pad kruisen. En bij experimenten waar stukjes geurspoor werden gewist vóór de tweede wandeling, maakten mieren voorspelbare fouten. Het lijkt er dus op dat mieren beter zijn in wiskunde dan veel mensen: inderdaad superslimme dieren.

Deze column verscheen vandaag in de Volkskrant.

Vroeger op de kleuterschool deden we wel eens een doorvertelspelletje. De juf fluisterde een zin in het oor van het meisje naast haar. Zij vertelde die zin dan weer door aan haar buurjongetje, enzovoorts. De laatste leerling moest de zin hardop zeggen, wat meestal tot hilariteit leidde, want de boodschap die aankwam was eigenlijk nooit de boodschap die was verzonden door de juf.

Dat geldt voor wel meer kanalen: er kan onderweg een boel gebeuren met gegevens. Denk aan ruis in een radiosignaal, atmosferische storingen die het signaal van een satelliet verstoren of krassen en stof op een cd. Hierdoor krijgt de ontvanger een boodschap waar hij niet alles of helemaal niets van begrijpt, of misschien zelfs eentje die iets heel anders zegt dan er bedoeld was.

Er zijn gelukkig wel manieren om ervoor te zorgen dat je er achter komt dat er iets mis is, en die manieren worden bestudeerd in de coderingstheorie.

De simpelste oplossing is het dubbel versturen van alle gegevens. In de kring met kleuters wordt de kans op een goede uitkomst groter als iedereen dezelfde boodschap twee keer doorfluistert in plaats van één. Helaas neemt de hoeveelheid data die verstuurd moet worden op deze manier danig toe.

Er zijn efficiëntere manieren om te ontdekken dat er onderweg iets mis gegaan is. Zo is een stuk tekst makkelijker te corrigeren dan een willekeurige rij cijfers: je herkent heus wel dat het woord “malkelijk” waarschijnlijk “makkelijk” moet zijn, maar als je “9789057122866” doorkrijgt, heb je geen idee of er een cijfer fout is. Dat betekent dat het handig is om af te spreken dat niet elk rijtje tekens toegestaan is in een boodschap.

Een handig middel is het toevoegen van een controlesymbool. Dat gebeurt bijvoorbeeld in het ISBN: het internationale identificatienummer van een boek. Niet elk getal van dertien cijfers komt voor als ISBN. Het boek dat nu voor mijn neus ligt heeft ISBN 978-90-5712-286-6. Daar zit redundantie in. De eerste twaalf cijfers betekenen allemaal iets: 978 betekent dat het een ISBN is, 90 staat voor het Nederlandse taalgebied, 5712 staat voor een bepaalde uitgeverij en 286 is het nummer van het boek.

(Een streepjescode van een boek met een ander ISBN.)

Dan is er nog één cijfer over, en dat wordt berekend aan de hand van de andere cijfers: de cijfers op de even plekken worden allemaal met drie vermenigvuldigd en bij elkaar opgeteld, en daar worden het eerste, derde, vijfde, zevende, negende en elfde cijfer nog bij opgeteld. In het voorbeeld: 3·7 + 3·9 + 3·5 + 3·1 + 3·2 + 3·6 + 9 + 8 + 0 + 7 + 2 + 8 = 124. Het laatste cijfer is dan, per afspraak, het verschil tussen dit getal en het volgende tiental: in dit geval, inderdaad, 6. Zo kun je direct herkennen dat 978-90-5712-296-6 geen geldig ISBN is.

Controlesymbolen komen ook voor in bankrekeningnummers, het betalingskenmerk op accept-giro’s en in burgerservicenummers. Dit soort trucs, en wat ingewikkeldere versies, zorgen ervoor dat ons dataverkeer betrouwbaar is, en dat veel foutjes die onderweg ontstaan zijn worden ontdekt, en soms zelfs verbeterd kunnen worden.

Deze column verschijnt vandaag in de Volkskrant.

Toen ik de gordijnen voor de babykamer bestelde, vroeg de dame achter de balie wel drie keer of ik alles écht goed gemeten had. Ik begon me een beetje zorgen te maken, ik had de lengte van de rails tot op de millimeter nauwkeurig gemeten, dat zou toch genoeg moeten zijn?

We zijn gewend dat kleine meetfouten nauwelijks een effect hebben. Een millimeter meer of minder maakt voor gordijnen echt niet uit. En als je in een recept 301 gram rijst gebruikt in plaats van 300 gram, dan zal de risotto heus niet ineens mislukken. Maar in sommige situaties kunnen heel kleine meetfouten grote gevolgen hebben. Dit verschijnsel, oftewel chaos, is door verschillende mensen herontdekt. Het mooiste vind ik het verhaal van Edward Lorenz.

Rond 1961 maakte Lorenz modellen om het weer te voorspellen. Met een (nogal primitieve) computer tekende hij (nog primitievere) grafiekjes van hoe variabelen als luchtdruk of luchtstromen in de loop der tijd veranderden. Op een gegeven moment wilde hij een bepaalde simulatie eens wat verder doorrekenen. Om tijd te besparen liet Lorenz de computer niet weer alles vanaf het begin uitrekenen. Hij nam de uitdraai van de vorige simulatie en gebruikte de gegevens die hij daar halverwege had gekregen als beginwaarden, dan kon de computer vanaf daar verder gaan.

Tot zijn grote verbazing zag hij (nadat de computer een uur flink had staan rekenen) dat er na enkele stappen een compleet ander patroon ontstond dan in de vorige simulatie. Lorenz had verwacht dat zijn programma vanaf dezelfde invoergegevens precies hetzelfde resultaat zou geven. Hij snapte er niets van: was zijn computer soms stuk?

Edward Lorenz net voordat hij chaostheorie ontdekte

Na een tijdje besefte hij dat de invoergegevens de tweede keer níet precies hetzelfde waren als tijdens de eerste simulatie. De computer rekende met zes cijfers achter de komma, maar op de uitdraai stonden alleen de eerste drie cijfers na de komma afgedrukt. Lorenz had bij de tweede simulatie daardoor in plaats van 0,506127 de waarde 0,506 ingevoerd. Een verschil zo klein dat je niet verwacht dat het iets uitmaakt.

Maar in de vergelijkingen die het weer beschrijven speelt zo’n verschil wél een belangrijke rol: een heel kleine verstoring aan het begin kan grote gevolgen hebben. Dit verschijnsel heet chaos en het komt voor bij allerlei systemen, met het weer als bekendste voorbeeld. Het gedrag van dit soort systemen is compleet vastgelegd door een aantal vergelijkingen en tóch zijn ze onvoorspelbaar, doordat ze zo gevoelig zijn voor kleine veranderingen in de beginwaarden. Lorenz suggereerde de metafoor van het vlindereffect (the butterfly effect): een vlinder in Stadskanaal die zijn met zijn vleugel slaat, kan een orkaan veroorzaken in Brazilië. Chaos verklaart waarom we het weer niet verder dan een week vooruit kunnen voorspellen: zelfs de meest nauwkeurige meetapparatuur zal afrondfouten maken.

De gordijnen hangen er zoals te zien keurig bij.

Gelukkig treedt er geen chaos-effect op bij het meten van gordijnen.  Ondanks eventuele meetfouten ziet de babykamer er nu prachtig uit. Nu maar rustig wachten op de chaos die de baby zelf straks gaat veroorzaken.