Wiskundemeisjes
Archief voor categorie 'Kunst'
Deze column verscheen afgelopen zaterdag in de Volkskrant.
Beste Judith de Leeuw,
In de kerstvakantie was het tijd voor achterstallige zaken: huis opruimen, boeken lezen, tv-programma’s kijken waar ik nog niet aan toegekomen was. Zo zag ik op uitzending gemist je documentaire “Overal spullen”. Herkenbaar, ook in mijn huis liggen overal spullen (vandaar dat opruimen). Maar jij pakte het heel wat rigoreuzer aan. (Ik mag wel jij zeggen toch? Je bent tenslotte ongeveer even oud als ik, al werd je op grond van je spullen door verschillende mensen als ergens in de veertig of zelfs in de categorie “oude hippie” ingedeeld.) Je deed het heel systematisch, wiskundig zelfs. Je ging namelijk al je spullen tellen.
Dat is natuurlijk precies waar getallen voor bedoeld zijn. Dingen tellen. Vee, mensen, appels, noem maar op. Op het moment dat mensen hoeveelheden met elkaar willen vergelijken, worden getallen belangrijk. Lang geleden eerst als kerfjes in een stukje hout of botje (en elk kerfje correspondeerde dan met een ding, zoals wij nog steeds wel behaalde punten turven), uiteindelijk de getallen zoals wij die nu gebruiken.
Behalve geteld heb je je spullen ook gecategoriseerd. Net als wiskundigen, biologen en verzamelaars hebben nu ook de hippe mensen hun neiging tot categoriseren ontdekt. Een geweldig voorbeeld zijn de “voor”- en “na”-foto’s van opruimtaferelen van de Zwitser Ursus Wehrli. Nog een boek om te kopen: “Opruimen, dat is de kunst”. Alleen ruimt Wehrli niet gewoon zijn huis op, maar eigenlijk alles. Een bord soep met lettervermicelli, bijvoorbeeld. Met als “na”-foto een bord soep waar de vermicelli netjes op alfabet ligt. En een slordig bakje frites met een klodder ketchup wordt een leeg bakje met een kloddertje ketchup ernaast, en de frietjes zijn geordend als geturfde streepjes. Ook kunst ruimt hij op: de opgeruimde slaapkamer van Van Gogh, de gesorteerde vierkantjes van Paul Klee en het in elkaar geperste blikje Campbell Soup zijn briljant.

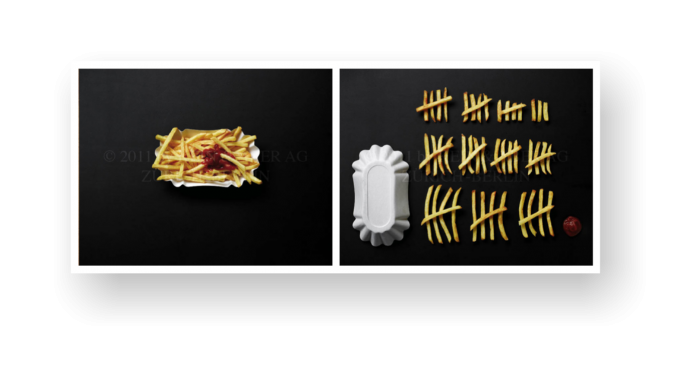
Twee voorbeelden van opruimprojecten van Ursus Wehrli.
Maar spullen. Het zijn er zoveel dat tellen een hels karwei is. Zoveel dat je ze niet binnenshuis kunt tellen: ze nemen teveel ruimte in (lengte keer breedte keer hoogte). In de loods waar je alles naast elkaar legt, heb je achteneenhalf keer de oppervlakte van je huis nodig om alle spullen kwijt te kunnen.
Jij hebt 15734 spullen, samen met je vriend en kind. Je hebt elk puzzelstukje, elke sok, elke pion, elk meubel geteld. 116 van die spullen zijn spullen om andere spullen in mee te nemen. Er zijn 123 spullen kapot. Je hebt 876 boeken, 312 platen en cd’s, 870 dingen om aan te trekken. Er zijn 45 dubbelen. En inmiddels zijn er misschien al wel wat spullen bijgekomen, al las ik op je weblog dat er een inbreker is langsgeweest die een aantal spullen uit de categorie electronica heeft meegenomen. Treurig, vooral vanwege de niet-spullen: je bestanden.
Hoeveel spullen heeft een mens nodig? Geen 15734. Het punt waarop je precies genoeg had is ongemerkt gepasseerd, zeg je. Bij mij ook, denk ik. Mijn goede voornemen met betrekking tot spullen: de verhouding gelezen staat tot ongelezen boeken in mijn kast vergroten. Meer lezen dan kopen, dus.
Met opgeruimde groeten,
Jeanine
Aanvulling na reacties van oplettende lezers: ik hoef natuurlijk niet per se meer te lezen dan te kopen om die verhouding te vergroten, als ik bijvoorbeeld zorg dat de verhouding gelezen : ongelezen boeken bij de nieuwe boeken groter is dan nu bij de oude boeken gaat dat uiteraard al goed. Dank! Mijn voornemen is natuurlijk wel om de verhouding zoveel mogelijk te vergroten, en dan is meer lezen dan kopen wel een goed idee.
Deze column verscheen afgelopen zaterdag in de Volkskrant.
Beste kunstrovers,
Een knap staaltje werk heeft u laatst geleverd in de Kunsthal. Het lukte u om – terwijl de schilderijen van buiten in het zicht hingen! – zeven kunstwerken van de muur te halen en die naar buiten te dragen. En niet de minste ook: Gauguin, Matisse, Picasso, noem maar op. De dag dat het nieuws bekend werd liep ik zelf in het Kunsthaus in Zürich naar schilderijen van precies deze grootheden te kijken. Om van kunst te genieten hoef je hem niet te stelen.

Een van de gestolen schilderijen.
Dus waarom kunst stelen? Omdat het veel waard is, natuurlijk! De schilderijen die u gestolen hebt zijn samen, las ik op nu.nl, tussen de vijftig- en honderdmiljoen euro waard. Een indrukwekkend bedrag, daar wilt u wel wat risico voor lopen. Maar wacht eens even: tussen de vijftig- en honderdmiljoen? Wat is dat nou voor een schatting? Daar zit een factor twee tussen! Dat is alsof een makelaar zegt: “Ik kan uw huis verkopen, het is tussen de tweehonderd- en vierhonderdduizend euro waard.” Die makelaar wijzen we allemaal snel de deur.
Bij huizenprijzen is het natuurlijk makkelijker. Vaak staan er vergelijkbare huizen in de buurt die recent nog zijn verkocht, daar kun je een redelijke schatting op baseren. Kunstwerken echter komen soms decennia lang niet op de markt, en er zullen veel minder vergelijkbare objecten te vinden zijn. Misschien speelt in de kunstwereld ook een beetje het principe: het is maar wat de gek ervoor geeft. Wat in de mode is, waar anderen ook in investeren, hoeveel media-aandacht er is voor de kunstenaar in kwestie: het speelt allemaal mee. De duurste kunstwerken van Damien Hirst bijvoorbeeld stegen een factor negen in prijs tussen 2000 en 2008, maar dit voorjaar waren ze nog maar 3,5 keer zoveel waard als in 2000. Dat zijn behoorlijke fluctuaties. Dan is het logisch dat een schatting geven erg moeilijk is.
Ook bij huizen is het lastiger geworden door de crisis: op dit moment staan er zóveel huizen te koop dat het maar de vraag is of veel schattingen niet achterhaald zijn. Als niemand je huis wil hebben voor een bepaalde prijs, dan is het dat blijkbaar niet echt waard. Denk ik dan, als leek in de economie.
Ook uw buit is natuurlijk onverkoopbaar. Niet omdat niemand hem zou willen hebben, maar zodra een kunstkenner zo’n schilderij tegenkomt is het uit met de pret. Veel waard, ja, maar u heeft er niets aan. Waardeloos.
Dus wat gaat u in hemelsnaam doen met die mooie schilderijen? Losgeld vragen? Een deal sluiten met de verzekering? Of heeft u de schilderijen misschien gestolen in opdracht van een rijke, eenzelvige, niet-chantabele kunstliefhebber die ze opbergt in een geheime kluis om ze elke avond voor het slapen gaan even te bekijken en ze nooit meer naar buiten te laten komen?
Ik hoop maar dat uw buit snel weer opduikt en terug kan naar de Kunsthal, zodat we weer allemaal kunnen zien waarom kunst écht waardevol is: de esthetische, historische, maatschappelijke en inspirerende waarde. En aan een schatting van de nieuwe beveiligingskosten waag ik me maar niet.
Met verontwaardigde groeten,
Jeanine
Deze column verschijnt vandaag in de Volkskrant.
Op allerlei onverwachte plekken kom je wiskunde tegen, zelfs op vakantie. Zo was ik laatst in Barcelona en, zoals het goede toeristen betaamt, gingen we de Sagrada Familia bezichtigen.

Al sinds 1882 wordt er aan de Sagrada Familia gebouwd, in 1883 kreeg architect Antoni Gaudí (1852 – 1926) de leiding. Gaudí is ook verantwoordelijk voor Park Güell (en indirect dus ook voor al die gemozaïekte salamanders die je in Barcelona op elke straathoek kunt aanschaffen).
Gaudí werkte tot zijn dood fanatiek aan de Sagrada (hij ging zelfs op de bouwplaats wonen!) en maakte een heleboel maquettes en schetsen. Helaas is veel verloren gegaan door een brand tijdens de Spaanse burgeroorlog, dus moesten de latere architecten reconstrueren wat Gaudí van plan was, en de rest zelf aanvullen met nieuwe plannen.
Een hoog gebouw met veel torens en ingewikkelde gewelven bouwen, is niet gemakkelijk. Hoe zorg je er bijvoorbeeld voor dat de pilaren en gewelven stabiel staan?
Gaudí verdiepte zich onder andere in de kettinglijn. Een kettinglijn is de vorm die een ketting aanneemt als je hem vrij laat hangen en alleen aan de uiteindes vasthoudt. Op het moment dat de ketting stilhangt, is een evenwichtstoestand ontstaan tussen de drie krachten die op elke schakel werken: de zwaartekracht en de twee spankrachten (links en rechts). Op dat evenwichtsmoment zijn er in die ketting alleen trekkrachten aanwezig in de richting van de ketting zelf.
Als je zo’n kettinglijn op de kop zou zetten, zouden alle drukkrachten dus ook precies in de richting van de boog zelf lopen, waardoor er niet van bijvoorbeeld opzij aan de boog getrokken wordt en hij dus heel stevig staat. De kettinglijn is al bekend sinds de zeventiende eeuw (onder andere Christiaan Huygens en Galileo Galilei hielden zich ermee bezig).
Maar een gewelf is ingewikkelder dan een poort of boog, die in principe maar twee-dimensionaal zijn. Voor een boog kun je nog redelijk eenvoudig controleren of hij in evenwicht is: je kijkt of je een kettinglijn kunt maken die (op de kop) dezelfde vorm heeft als de boog die je in gedachten had.
Voor het ontwerpen van een gewelf moet je drie dimensies gebruiken. Je kunt daar een beetje mee smokkelen door naar dwarsdoorsnedes te kijken, maar echt drie-dimensionaal aan krachten rekenen is ingewikkeld. Gaudí gebruikte verschillende methodes, maar de tofste vind ik zijn hangende modellen. (Die gebruikte hij niet voor de Sagrada trouwens, maar voor een ander kerkontwerp.) Gaudí maakte van een heleboel touwtjes met gewichtjes eraan een op zijn kop hangend kerkgewelf. Oftewel: hij ontwierp het gewelf direct op stabiliteit. En door te variëren met touwtjes en gewichtjes kon hij het ontwerp meer naar zijn zin maken.

Behalve een replica van een indrukwekkend hangend model is in het museum bij de Sagrada Familia nog meer wiskunde te zien: Gaudí gebruikte kegelsnedes zoals parabolen en hyperbolen in zijn ontwerpen, en op de Sagrada staat ook nog eens een magisch getallenvierkant, waarin de som in alle rijen, kolommen, diagonalen en nog wat van die dingen steeds weer 33 is, de leeftijd van Jezus toen hij werd gekruisigd.

Al met al een aanrader voor de wiskundige toerist!
Ik heb dit jaar getwijfeld of ik mee zou doen aan de Dance your PhD contest. Ik zag al een showballet met kettingbreuken voor me, maar bedacht net op tijd dat ik zelf eigenlijk niet zo goed kan dansen.
Maar...knopenkoning Roland van der Veen kan wél dansen en besloot om bij de verdediging van zijn proefschrift samen met zijn paranimfen een dans te doen. Hoe cool is dat?
Roland heeft twee filmpjes online gezet. Het eerste laat zijn lekenpraatje zien, waarin Roland uitlegt hoe je vlechten tegenkomt bij het roeren in een kopje koffie en hoe je dat zelfde beeld kunt gebruiken om te begrijpen hoe de kwantumcomputer werkt.
Aan het einde van het filmpje (voor wie nog niet gelijk heeft gekeken) poneert Roland zijn belangrijkste stelling:
Wiskunde is een uitvoerende kunst.
En vervolgens danst hij samen met zijn paranimfen een Tango en een Lindy Hop (een Lindy Hop!) met linten in de hand. Ze leggen al dansend een knoop in de linten, net als de kwantumdeeltjes dat doen. Daarna volgt nog een korte indruk van de werkelijke verdediging van zijn proefschrift.
We feliciteren Roland van harte met zijn doctorstitel en hopen dat hij wiskunde en dans nog vaker zal combineren!
In de gangen van het EWI van de TU Delft hangt sinds kort wiskundige kunst. Op de 7de en 9de verdieping kan iedereen genieten van werken gebaseerd op de Stelling van Van der Waerden.

Deze tekst hangt er bij de kunstwerken:
Partitioning the first \(\) natural numbers into \(\) subsets not containing arithmetic progressions of length \(\)?
The famous Van Der Waerden theorem shows that this is possible only up to a certain number. Many mathematicians worked on its exact location, which is considered as a hard problem. Lower bounds are provided by actual presenting such partitions, called certificates. A breakthrough in finding such certificates was forced at Delft by combining SAT technology and two dimensional visualization methods initiated by Marijn Heule. Beautiful pictures arise, showing many symmetries. This is the more surprising considering they represent structures not allowing arithmetical regularities.

De werken zijn gemaakt door kunstenares Mieke Schobbe.
In 2007 schreef K.P. Hart voor het Nieuw Archief voor Wiskunde een mooi artikel over de stelling van Van der Waerden (pdf).
Met dank aan Hans van Maaren voor de tip.
Via kennislink kwam ik terecht op deze website, waar je een Escherachtige print ziet die je kunt bewegen! Om een beetje duizelig van te worden. Klik en sleep met de muis.
Tribute to Escher in Barcelona
Martijn stuurde ons een link naar deze bijzondere pi-ketting. Van RGB Laboratory, zo te zien alleen te koop in Japan.

Vorig jaar schreef ik hier over een standbeeld van een multigrid olifant, naar aanleiding van een tip van Peter van Emde Boas.

Bij mijn promotie overhandigde dezelfde Peter me een prachtig (en ik citeer) "existentiebewijs van de kleinere versie". Supergaaf! Ik wilde hier al een tijdje een foto plaatsen, maar ik had steeds iets anders aan mijn buik hoofd. Gelukkig kwam Jeanine deze week op visite en maakte zij eindelijk een foto van mij met mijn mooie multigrid olifant.

Als je zelf ook zo'n toffe olifant wilt, dan moet je vooral even contact opnemen met de Elephant Parade Shop (of Peter voortaan uitnodigen voor al je feestjes).
Een bijzonder knap staaltje van rijmen in het Engels! De geschiedenis van de Riemann-hypothese in liedvorm, geschreven door Tom Apostol. Met een wijze les voor wiskundigen aan het eind. Briljant!
 Internetbureau Rotterdam
Internetbureau Rotterdam 

