Wiskundemeisjes

Deze column verscheen afgelopen weekend in de Volkskrant.

Beste Jamie Oliver,

Deze week maakte ik je recept voor geblakerde kip met quinoa-salade. Een heerlijke maaltijd, daarover heb ik niets te klagen. Maar ik vond het wel jammer dat ik die avond een stuk langer in de keuken stond dan gepland. Ik haalde het recept uit je boek Jamie in 15 minuten. De maaltijden in dat boek zouden stuk voor stuk binnen vijftien minuten op tafel moeten staan, ideaal dus voor een doordeweekse avond. Ik nam de proef op de som toen ik om zes uur hongerig uit mijn werk gerend kwam.

Zoals je boek voorschrijft zette ik eerst alle ingrediënten, pannen en andere keukenspullen netjes klaar. Zelfs het kokend water moet klaarstaan voor die bereidingstijd van vijftien minuut ingaat. Waarom is me een raadsel. Tien minuten haastig zoeken naar piment en de juiste opzetstukjes voor de keukenmachine telt toch gewoon mee als tijd die je nodig hebt om het eten te bereiden?

Alle stond klaar, de tijd ging in en het echte werk begon. Quinoa wellen, allerlei kruiden in de keukenmachine hakken, kip marineren, platslaan en bakken. Toen waren de vijftien minuten ruim om en ik was nog niet eens op de helft van het recept. Daarna moest ik nog paprika’s, mango en avocado snijden. (Als schrale troost zag ik in het instructiefilmpje op je site dat het andere mensen ook ongeveer anderhalve minuut kost om een mango te snijden.) Uiteindelijk had ik vanaf het moment dat ik begon met koken drie kwartier nodig om de maaltijd op tafel te krijgen. Met het klaarzetten van de spullen erbij kwam ik op bijna een uur. Dat is wel wat meer dan die beloofde vijftien minuten.

Uit recensies op bol.com blijkt dat ik niet de enige ben met dit probleem. Iemand schrijft hoopvol: “lekkere combinaties die na wat oefening in dertig minuten te maken zijn”. Een ander heeft de moed opgegeven en verzucht: “Je bent alleen al een kwartier bezig om de aanwijzingen te begrijpen en in juiste volgorde te zetten.”

Vandaar, beste Jamie, mijn vraag: hoe lang duurt een minuut bij jou? Gebruik je soms een obscure Britse meeteenheid? Ik weet dat jullie Engelse pond minder is dan een halve kilo en jullie pint juist iets meer dan een halve liter. Moeten we voor een minuut van jou misschien twee of meer van onze minuten rekenen? Dat zou een hoop verklaren.

Overigens zie ik een trend in je werk. In 2008 stond voorop je boek Jamie’s kookrevolutie “Écht iedereen kan leren koken in 24 uur” (en inderdaad, in een volledig etmaal moet het zelfs de grootste kluns lukken om één zo’n recept te bereiden). Daarna volgde Jamie in 30 minuten, de telefoon-app met recepten in 20 minuten (recepten die de argeloze amateur al snel een halve avond kostten) en nu dus Jamie in 15 minuten. Je ging dus stapje voor stapje van vierentwintig uur naar vijftien minuten. Ik hoop dat deze dalende lijn zich voortzet en dat er volgend jaar een boek Jamie in 3 minuten verschijnt. Die recepten kunnen gewone stervelingen als ik dan waarschijnlijk in een half uur op tafel krijgen. Dat moet net lukken op een doordeweekse avond.

Smakelijk,

Ionica

ps Dit is het recept (let ook op de woordspeling in de titel): Ge­bla­ker­de kip san fran-quinoa­sa­la­de. Laat me jullie recordtijden weten!

Deze column verscheen afgelopen weekend in de Volkskrant.

Geachte manager van hotel De Biltsche Hoek,

Laatst was ik op zoek naar een hotel in Utrecht, liefst lekker dichtbij de Domtoren. Toen belandde ik op uw website met foto’s van ruime kamers, een gezellige hotelbar en een uitnodigend zwembad. En dat alles “op een steenworp afstand van de bruisende stad Utrecht” zoals u op uw website schrijft. Dat moet dus wel heel dichtbij zijn. Want hoever kan een steenworp nou helemaal zijn?

Gezellige hotelbar, en dat op een steenworp van de stad Utrecht

Zelf gooi ik (vanzelfsprekend) als een meisje en ik kom met een steen niet verder dan een meter of zeven. Ik zocht op wat het wereldrecord steenwerpen eigenlijk is. Helaas is daar weinig van bekend, het is niet zo’n populaire wedstrijdsport. In 1906 was steenwerpen voor het laatst een onderdeel op de Olympische Spelen. Toen haalde de Griekse atleet Nikolaos Georgantas goud met een worp van 19,925 meter. Dat is ook niet zo ver. Maar die worp was met een flinke steen van zes kilo, oftewel zo’n driehonderd hotelzeepjes.

Laten we daarom aannemen dat u met uw steenworp de oude Noorse eenheid steinkast bedoelt. Daarvan denken historici dat het een afstand tussen de veertig en zestig meter is. Dus uw hotel ligt op een meter of zestig van de stad Utrecht. Dat betekent dat ik na een lange nacht in uw gezellige hotelbar de volgende dag kan kruipen naar de Domtoren.

Tot mijn verbazing zag ik echter op de kaart dat uw hotel bijna zes kilometer van de Domtoren afligt. Dat is meer dan een uur kruipen! De Biltsche Hoek staat in in een uithoek van De Bilt (zoals de naam misschien al een beetje verraadde).

Teleurgesteld besloot ik uw hotel niet te boeken. Als die steenworp niet klopt, dan zijn die kamers waarschijnlijk ook niet zo ruim en die hotelbar niet zo gezellig. Maar toen bedacht ik dat uw hotel misschien wel heel hoog is. Zó hoog, dat als je er een steen van afwerpt, je makkelijk de domtoren raakt. Hoe hoog zou De Biltsche hoek dan moeten zijn?

Ik sloeg aan het rekenen. Om u te matsen nam ik aan dat er geen luchtweerstand is en dat er een supergoede werper op het dak van het hotel staat. Bij honkbal gooien de beste spelers de bal weg met een slordige honderdvijftig kilometer per uur.

Met die snelheid kost het de bal 144 seconden om de afstand van uw hotel naar de Domtoren af te leggen (in het zeer hypothetische geval dus dat er geen luchtweerstand is). Om 144 seconden te vallen zonder de grond te raken, moet uw hotel dan ruim honderd kilometer hoog zijn. Honderd kilometer! Hoeveel kamers kunt u daarin kwijt? Daarbij vergeleken is zelfs de hoogste wolkenkrabber van Dubai een dwerg met een schamele achthonderd meter.

Maar hoe meer ik er over nadacht, hoe minder waarschijnlijk het me leek dat er zo’n gigantisch hotel in Utrecht staat zonder dat ik het ooit gezien heb. Voor de zekerheid boekte ik een ander hotel. Dat lag op 48 meter van de Domtoren, een steenworp zeg maar. Al zeiden zij daar op hun website dan weer niets over.

Verbaasde groet,

Ionica

Deze column verscheen afgelopen weekend in de Volkskrant.

Beste winkeliers van Nederland,

De benzineprijzen zijn naar recordhoogte gestegen, luxe-artikelen werden nog snel ingeslagen, en de consument schijnt per 1 oktober de hand op de knip te houden: per afgelopen maandag werd het hoge btw-tarief, de btw op luxe producten en diensten, verhoogd van 19 naar 21 procent. Geen mooi vooruitzicht voor uw inkomsten! Daar moest u iets op verzinnen.

Dus haalde u eind september nog snel even de aloude btw-kortingsacties van stal, nu de korting die u moest geven nog enigszins te overzien was. Tijdens dergelijke acties hoeven uw klanten tijdelijk geen btw te betalen. Niet echt natuurlijk, want op elke transactie wordt gewoon btw geheven, maar het bedrag dat normaal gesproken de btw zou uitmaken wordt nu omgezet in een korting.

Zo las ik bijvoorbeeld op een autoverkoopwebsite: “Citroën neemt in september de btw van de C4 en de C4 Picasso voor haar rekening. Dat betekent dat je een korting van 19 procent op de nieuwprijs krijgt.” Hetzelfde geldt voor de 21 procent korting die de Formido begin oktober nog belooft op een product naar keuze (“21% btw? Daar doen we (nog) niet aan mee! Nu 21% korting!”).

19 Procent korting, dat is nogal wat! Het is zelfs méér dan de btw die u beweert aan uw klanten cadeau te doen. Reken maar na. We bekijken een auto die – even voor het gemak – 10.000 euro kost exclusief btw. Daar kwam in september dan nog 19 procent btw bij, oftewel 1.900 euro, zodat de kostprijs normaal gesproken 11.900 euro zou worden.

Nu gaf u 19 procent korting. Dat is 0,19 x 11.900 = 2.261 euro. Veel meer dus dan de 1.900 euro die aan btw betaald zou moeten worden. De consument hoefde nog maar 9.639 euro te betalen, terwijl de auto exclusief btw 10.000 euro kost. Hoe dat komt? Nou, het btw-percentage van 19 procent is een percentage van de kale prijs zonder btw, terwijl de korting van 19 procent een percentage is van de hogere totaalprijs inclusief btw.

Het is dus eigenlijk helemaal niet verstandig te stunten met 19 of 21 procent korting, zoals de Citroënverkoper respectievelijk de Formido doen, want dat kost u meer dan alleen de btw. Maar de meesten van u begrepen dit best.

De Mediamarkt bijvoorbeeld, die stuntte met de slogan ‘19% btw Weg ermee!’ Hoeveel korting gaf u dan eigenlijk, als u de btw weghaalde? We kijken weer even naar die auto. De btw bedroeg 1.900 euro op het totaalbedrag van 11.900 euro. Dat is dus 1.900/11.900 x 100 procent, oftewel ongeveer 16 procent, van de totaalprijs. Om de btw te compenseren, hoefde u dus maar 16 procent korting te geven.

Slim van u dus, die slogan ‘19% btw Weg ermee!’. Helemaal correct, en de 19 procent bleef hangen in mijn hoofd. U klonk dus erg gul en intussen gaf u gewoon de 16 procent korting die het btw-bedrag bedroeg. En klanten die boos komen klagen dat ze geen 19 procent korting hebben gekregen, maar slechts 16, kunt u doorverwijzen naar de vragensectie op uw actiesite, waar het bovenstaande verhaal haarfijn wordt uitgelegd. Mijn welgemeende complimenten!

Met oplettende groeten,
Jeanine

Dit stuk staat vandaag in de Kennisbijlage van De Volkskrant. Helaas werkt de link in dat artikel niet meer, onderaan dit stuk staat de goede link naar meer informatie.

Morgen wordt wereldwijd pi-dag gevierd. Elk jaar verzamelen pi-liefhebbers zich in de derde maand op de veertiende dag (oftewel: 3,14) voor een feestje. Tijd om de grootste misverstanden over deze wiskundige constante recht te zetten.

1. Pi heeft iets te maken met de stelling van Pythagoras.
In de kerstuitzending van Bananasplit kwam pi ter sprake. Danny de Munck gaf onmiddellijk toe dat hij niets wist van wiskunde. Naast hem zat Nance, zij had ook geen wiskundeknobbel, maar “wist nog wel dat pi de stelling van Pythagoras is”. Helaas, pi en de stelling van Pythagoras zijn de twee dingen die de meeste mensen onthouden hebben van wiskunde, maar ze hebben niets met elkaar te maken. De stelling van Pythagoras gaat over driehoeken, terwijl pi van cirkels komt. Pi is de omtrek van een cirkel gedeeld door de diameter: ongeveer 3,14. Het maakt niet uit hoe groot of klein de cirkel is, de verhouding tussen omtrek en diameter is altijd precies pi. Daarnaast verschijnt pi ook op allerlei andere plaatsen: bijvoorbeeld in de verdeling van schoenmaten.

2. Pi is precies 3,14.
Pi begint als 3,14159 en daarna volgen nog oneindig veel cijfers. In die cijfers zit geen regelmaat. In de praktijk wordt daarom altijd een benadering van pi gebruikt. In de bijbel laat Solomo voor een tempel een bekken maken: “vijf el hoog, met een middellijn van tien el en een omtrek van dertig el”. Volgens deze tekst is pi dus gelijk aan 30/10 = 3, een eenvoudige benadering. Hoe nauwkeuriger de berekening, hoe meer decimalen er nodig zijn. Pi is niet te schrijven als een breuk, maar kan wel goed benaderd worden met breuken. Op school wordt vaak 22/7 (ongeveer 3,14285) gebruikt voor pi.

3. In de Amerikaanse wet staat dat pi gelijk is aan 3.
Het is een vaak voorkomend misverstand dat een bijbelvaste Amerikaanse staat in de wet heeft vastgelegd dat pi drie is. Zoiets is nooit gebeurd of zelfs maar voorgesteld. Wel is in 1897 in Indiana een merkwaardig wetsvoorstel ingediend door een amateurwiskundige. Hij wilde pi anders definiëren om berekeningen makkelijker te maken. In zijn voorstel waren allerlei verschillende waarden voor pi te vinden, variërend van 3,2 tot 4(!). Het voorstel werd in eerste instantie unaniem aangenomen, maar het sneuvelde alsnog in de senaat. Niet omdat de senaatsleden vonden dat er iets mis was met de theorie, maar omdat ze dachten dat pi geen zaak van wetgeving was.

4. In pi zitten geheime boodschappen verstopt.
Het zoeken naar gecodeerde boodschappen in de oneindige reeks decimalen van pi is een populaire hobby. Door de cijfers om te zetten naar letters kun je zinnen als “God bestaat” in de decimalen ontdekken. Het probleem is dat wiskundigen vermoeden dat elk rijtje cijfers uiteindelijk een keer in de decimalen van pi voorkomt, dus dan zou ook de zin “God bestaat niet” vanzelf een keer in de decimalen opduiken, net als de integrale tekst van Hamlet of de Volkskrant van vandaag. Voor wie het moeilijk te geloven vindt dat in één getal alle mogelijke teksten zijn gecodeerd: er is een getal waarvan we dit zeker weten dat alle mogelijke codes er instaan. Dat is de contante van Champernowne: 0,12345678910111213141516... enzovoorts. Niets magisch aan dus.

5. Het is belangrijk om pi zo ver mogelijk uit te rekenen.
Al eeuwenlang is het een sport om zoveel mogelijk decimalen van pi uit te rekenen. Omdat het er oneindig veel zijn, valt het record steeds weer te verbeteren. Zhu Chongzi berekende bijvoorbeeld rond het jaar 500 al dat pi tussen 3,1415926 en 3,1415927 ligt. Op dit moment staat het record op 2,7 biljoen cijfers. Om een indruk te geven hoe belachelijk veel cijfers dit zijn: als je deze 2,7 biljoen cijfers gaat opzeggen (zeg één per seconde), dan duurt dat 85.616 jaar. Voor de meeste berekeningen zijn echter een stuk of tien cijfers na de komma ruim voldoende en niemand heeft meer dan duizend cijfers nodig.

Dat de records toch steeds sneuvelen heeft twee redenen. Allereerst hebben snelle rekenmethodes allerlei andere toepassingen, het uitrekenen van pi is niet meer dan een mooie test. Bovendien raakt het uitrekenen van zoveel mogelijk decimalen voor sommige mensen een obsessie. Zelfs Isaac Newton raakte in de ban van pi en schreef in 1666: “Ik schaam me om te vertellen tot hoeveel cijfers ik deze berekeningen heb uitgevoerd, toen ik niets anders te doen had.”

Tot en met 28 maart hangen de eerste miljoen decimalen van pi in de Centrale Bibiliotheek Rotterdam als onderdeel van een expositie over de geschiedenis van pi. Morgen wordt tussen 13.00 en 17.00 uur pi-dag gevierd met lezingen, wiskundige puzzels en pi-koekjes. De toegang is vrij. Adres: Bibliotheek Rotterdam, Hoogstraat 110, Rotterdam. Meer informatie op de site van de bibliotheek.

Zoals diverse lezers ons al mailden, kwam deze week de stelling van Pythagoras voorbij in Wie is de mol?. Kim Pieters moest de volgende opgave oplossen.

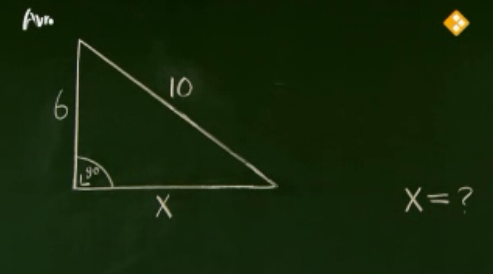
Ze begon gelijk over de stelling van Pythagoras en schreef op.

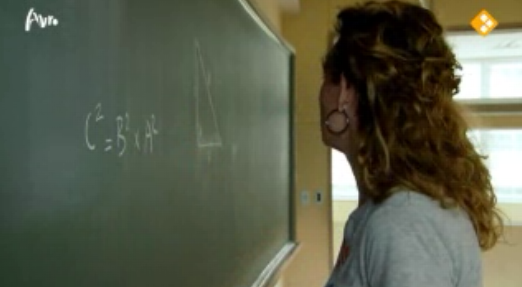
Overigens ging Kim deze formule niet invullen, maar begon ze daarna over de hoek van 90 graden. Nu mailden verschillende lezers ons dat alweer een BN-er niets weet van wiskunde. Maar Kim zei in het interviewtje na de opdracht al dat de stelling van Pythagoras natuurlijk is.

Het zou best zo kunnen zijn dat Kim de mol is en doet alsof ze niets van wiskunde weet, terwijl ze heimelijk de werken van Serre leest. Maar ik gok van niet. Ik volg dit jaar voor het eerst Wie is de mol? en heb het idee dat de kijker door de montage zoveel mogelijk op het verkeerde been wordt gezet. Ik denk nu dat Frits of Erik de mol is...

Je kunt de hele aflvering hier terugkijken. De opgave van Kim zit na ongeveer 13 minuten. Overigens was de scheikunde-opgave met water afmeten met verschillende emmers natuurlijk ook een wiskundesom.

Loïs tipte ons dat er in de kerstuitzending van Bananasplit flink werd gezwetst over pi. Nance wist gelukkig pre-cies wat is!

Danny de Munk: "Ik ben absoluut geen rekenwonder, mij kun je echt een oor aannaaien aan alle kanten."
Frans Bauer: "En jij, kun jij dat berekenen zo'n..."
Nance: "Ik wist wel dat de stelling van Pythogaras was, maar hoe je het berekent..."
Frans Bauer:"Dat is hardstikke makkelijk, je pakt gewoon de hoogte maal de lengte en dan pak je de middenas van de cirkel en dat vermenigvuldig je. [gevolgd door nog wat handgebaren en getallen]"

Oei. Voor alle BN-ers die deze site lezen en zich afvragen wat wel is: de omtrek van een cirkel gedeeld door de diameter. Dat is alles.

Hier kun je de hele aflevering terugkijken, het pi-fragment zit na ongeveer 54 minuten.

Trouwe lezer HJ wees ons op een leuk interview (de Volkskrant, 15 december) met Alexander Rinnooy Kan over allerhande belangrijke politieke zaken na het mislukken van het AOW-overleg. Maar hij vertelt ook iets over wiskunde:

Zelf weet Rinnooy Kan als geen ander dat het verstandig is je te blijven ontwikkelen. De wiskundige verliet op zijn 41ste de wetenschap. ‘De tragiek van de wiskundige is dat je vanaf je veertigste weinig nieuws meer kunt. Ik weet niet wat het precies is, maar je creativiteit, flexibiliteit of je vermogen slijt om lang en diep na te denken over abstracties. Het is een groot verdriet van menig wiskundige.’

Hoewel hij zich niet meer actief bezighoudt met wiskunde, heeft hij zijn passie ervoor behouden. Voor het eerst in het gesprek begint hij uitbundig te vertellen.

‘G.H. Hardy schreef daar zo’n prachtig boekje over! Pas op zijn 60ste beseft hij dat zijn creativiteit aan het verdwijnen is. Hij vindt zijn leven zinloos geworden. Maar het kan ook anders. Hardy beschrijft een prachtige anekdote over de Indiase wiskundige Ramanujan, die op zijn sterfbed ligt. Wiskundigen zijn niet de makkelijkste praters, dus Hardy zegt dat hij in een taxi zat met een nummer waar hij echt niks bijzonders in kon ontdekken, ik meen 1789.

‘‘Nee, nee Hardy, dat zie je verkeerd!’, zegt Ramanujan zonder een seconde na te denken en bijna overlijdend. ‘Het is het kleinste getal dat je op twee manieren kunt schrijven als de som van twee derde machten’.’

Rinooy Kan lacht. ‘Dat is toch fenomenaal! Het klopt, hè?’

Bijna goed! Het is een van onze favoriete anekdotes, maar het getal klopt natuurlijk niet.

HJ wees ons ook op een grappige ingezonden brief die de volgende dag verscheen:

Aftakeling

Hierbij een reactie op het interview met SER-voorzitter Alexander Rinnooy Kan (Economie, 15 december). Niet 1789 maar 1729 is het kleinste getal dat op twee manieren de som van twee derdemachten is (namelijk die van 10 en 9 zowel als die van 12 en 1). Ik ben een wiskundige van 65 jaar en nog zeer alert. Gelukkig geldt de aftakeling niet voor iedere wiskundige vanaf 40 jaar.

Ruud Engelschman, Rheden

Op deze site kun je meer lezen over de zogenaamde "taxicab-getallen" die naar de Hardy-Ramanujan-anekdote vernoemd zijn.

Vorig jaar vertelde Bill O'Reilly op het Amerikaanse Fox News hoe vreselijk Amsterdam is: iedereen gebruikt drugs, het is een paradijs voor criminelen, het is er levensgevaarlijk, enzovoorts.

Twee Amsterdammers maakten als antwoord hierop een filmpje met wat feiten over Amsterdam, zie the Truth About Amsterdam. Eén van die feiten was: 40,3% van de Amerikanen heeft cannabis geprobeerd, tegenover 22,6% van de Nederlanders.

Het antwoord van O'Reilly: "The way they use statistics in The Netherlands is different. Plus, it's a much smaller country."

Dit wiskundemeisje wist niet of ze moest lachen of huilen. Gelukkig staat er op  the Truth About Amsterdam een nieuw filmpje waar het nog een keer wordt uitgelegd.

Ze liggen in zulke grote stapels bij de boekwinkels dat je ze vast niet hebt gemist: de delen van de Millennium Trilogie, van de overleden Zweedse auteur Stieg Larsson ("Mannen die vrouwen haten", "De vrouw die met vuur speelde", "Gerechtigheid"). Normaal gesproken schrijven we hier natuurlijk niet zomaar over boeken die we gelezen hebben, maar als er wiskunde in voorkomt wel! Kort samengevat: de trilogie is heel spannend, en zeer geschikt voor de zomervakantie.

(Noomi Rapace als Lisbeth Salander in de verfilming van het eerste deel die in augustus uitkomt)

Ik zal niet teveel verklappen, maar Lisbeth Salander, een van de hoofdfiguren, is een jonge vrouw die er uitziet als een jongetje van veertien; gewelddadig, anti-sociaal en eigenzinnig is, extreem goed is met computers en gespecialiseerd is in persoonsonderzoeken. In het tweede deel, "De vrouw die met vuur speelde", leest ze een wiskundeboek: "Dimensions in Mathematics" van Dr. L.C. Parnault, Harvard University, 1999.

Voordat ze het artikel in "Popular Science" had gelezen, was ze nooit ook maar één seconde gefascineerd door wiskunde of had ze ook maar bedacht dat de tafels van vermenigvuldiging mathematiek waren. De tafels van vermenigvuldiging, dat was iets wat ze in een middag op school uit haar hoofd had geleerd en ze had maar niet kunnen begrijpen waarom de meester daar een heel jaar over was blijven doorzeuren.

Plotseling had ze de onverbiddelijke logica vermoed die achter de gepresenteerde redeneringen en formules moest zitten, wat haar naar de planken van de academische boekhandel had geleid. Maar pas toen ze "Dimensions in Mathematics" had opengeslagen, was er een heel nieuwe wereld voor haar opengegaan. Wiskunde was eigenlijk een logische puzzel met oneindige variaties; raadsels die konden worden opgelost. De truc was niet om rekenvoorbeelden op te lossen, want vijf maal vijf was altijd vijfentwintig. De truc was om de structuur te begrijpen van de verschillende regels die het mogelijk maakten om elk willekeurig wiskundig probleem op te lossen.

Lisbeth raakt in de ban van de laatste stelling van Fermat: de vergelijking heeft geen geheeltallige oplossingen als en , en allemaal niet nul zijn. Fermat beweerde in 1637 dat hij een mooi bewijs gevonden had, maar dat de kantlijn waarin hij schreef te klein was om het te bevatten. Uiteindelijk werd de stelling in de jaren '90 bewezen door Andrew Wiles. Maar zijn bewijs is zó modern, dat dat onmogelijk het bewijs kan zijn waarvan Fermat beweerde dat hij het gevonden had. Dus Lisbeth gaat erover nadenken.

Het is een beetje jammer dat de stelling van Fermat in het boek alleen maar voorkomt als het geval , want dat klopt gewoon niet. Het geval is veel makkelijker dan het algemene geval en werd veel eerder bewezen. Het is ook jammer dat de redacteur niet zo goed heeft opgelet: bij het begin van elk deel staat een vergelijking, en steeds zijn de kwadraten per ongeluk niet in superscript, maar gewoon op dezelfde regel afgedrukt, zodat er formules staan als .

Maar het wiskundige zijspoor is maar een heel klein onderdeel van het verhaal, en deze foutjes mogen de pret niet drukken. Zeker lezen dus, als je van spannende boeken en intrigerende personages houdt!

En bestaat dat fascinerende boek "Dimensions in Mathematics" nou echt? Nee, zo schrijft Harvard University Press zelf maar op de website:

Dimensions in Mathematics - a phantom, a chimera

Mystery Readers who will have snagged a copy of Steig Larsson's newest thriller The Girl Who Played with Fire (it's out in the UK, translated from the original Swedish; US edition is coming in July) will have noticed that female protagonist Lisbeth Salander satisfies her nascent interest in spherical astronomy with the help of a book titled "Dimensions in Mathematics," written by one L. C. Parnault and apparently published by Harvard University Press in 1999.

Unfortunately for those of you who would like to follow in Lisbeth's footsteps and penetrate the "dimensions of mathematics" for yourselves, you'll have to turn somewhere other than the work of the esteemed Dr. Parnault, for as far as we can tell, and if our memories and our computers have not completely failed us, HUP has in fact published no such work, in 1999 or at any other time. Thus it seems that Mr. Larsson, whose Scandanavian crime fiction has won him a good deal of posthumous fame, leaves us with more than just fictional mysteries. We can only speculate about what Dr. Parnault would have been like, had we actually known or published him, and as for the contents of his mythical "Dimensions," well, that's an even greater mystery. For all we know, it could be the key to the universe or something, and now it's gone missing! So if you've spied a copy of "Dimensions" in some musty back-alley secondhand shop, or know the whereabouts of our friend Dr. Parnault, or if somehow you yourself are Dr. Parnault, just, um, get in touch.

Gelezen op nu.nl:

De kwaliteit van lessen rekenen en wiskunde verschilt veel per basisschool. Bijna een kwart van de scholen presteert onder het gemiddelde en ruim een kwart doet het bovengemiddeld goed.

Dat de kwaliteit van rekenlessen sterk verschilt is natuurlijk wel nieuws. Maar dat het aantal scholen dat bovengemiddeld presteert ongeveer even groot is als het aantal dat ondergemiddeld presteert, lijkt ons minder bijzonder.