Dit bericht is geplaatst op zondag 6 april 2008 om 09:21 in categorieën Puzzels. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
IJstaart met glazuur
In Puzzels, door Ionica
Deze leuke puzzel hoorde ik Peter Winkler vertellen bij The Math Factor.

In een zeer koude kamer staat een ronde ijstaart met bovenop een laag chocoladeglazuur. Kies een willekeurige hoek α en snijdt een punt af met een hoek van α graden. Draai deze punt ondersteboven. Snijd daarnaast weer een punt van α graden af, draai ook deze om en ga zo door. Als je rond bent, dan ga je gewoon verder met snijden en omdraaien van punten. Bewijs dat voor elke gekozen α al het glazuur weer aan de bovenkant is na een eindig aantal keer snijden.
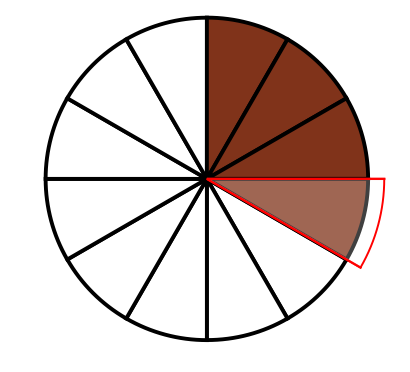
Als α een deler van 360 graden is, dan is het duidelijk dat het goed gaat: stel dat je α = 30 graden kiest. Dan snijd je twaalf punten af die je één voor één omdraait. Bij de tweede ronde snijd je precies op dezelfde plaatsen als eerst en draai je de punten weer één voor één terug. Na vierentwintig keer snijden is al het glazuur dus weer aan de bovenkant.
Maar waarom werkt het ook als α geen deler van 360 is? En zelfs als α irrationaal is?
Wij moesten hier zelf best een tijd op puzzelen. Lezers die er niet uitkomen, kunnen naar het Mathematisch Instituut komen met een taart en een mes. Onze collega's Jos, Sierk en Arjen zijn bereid een demonstratie te geven in ruil voor een stuk taart!
 Internetbureau Rotterdam
Internetbureau Rotterdam 
