Dit bericht is geplaatst op zaterdag 15 mei 2010 om 09:59 in categorieën Column. Je kunt de reacties volgen via een RSS 2.0 feed. Je kunt een reactie plaatsen, of een trackback van je eigen site plaatsen.
Wiskundemeisjes
Ionica & Jeanine
Gênante vragen
In Column, door Ionica
Deze column verscheen vandaag in de Volkskrant.
Mijn vriendin Cristel studeerde geschiedenis met als specialisatie achttiende-eeuwse dagboeken. Op feestjes belandt ze steevast naast iemand die werkelijk alles weet van de Peloponnesische oorlog. Als zo iemand hoort dat zij een historica is, dan verwacht hij dat ze daar uren met hem over kan praten. Cristel vindt het dan altijd een beetje gênant om toe te moeten geven dat zij helemaal niets weet van de Peloponnesische oorlog.
Als wiskundige kom je bijna nooit in zulke situaties, omdat de meeste mensen bij wiskunde niet verder komen dan de stelling van Pythagoras. Daarom was ik zo verbaasd toen iemand laatst op een borrel aan me vroeg hoe het zat met het vermoeden van Collatz.
Ik wist gelukkig wel wat het vermoeden van Collatz was. Het gaat over reeksen getallen. Je begint met een willekeurig geheel getal, groter dan nul. Als het getal even is, dan deel je het door twee. Als het getal oneven is, dan vermenigvuldig je het met drie en tel je er één bij op. Daarna herhaal je dit proces met de uitkomst, en opnieuw, en opnieuw.
Bijvoorbeeld:
6 -> 3 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1
of
13 -> 40 -> 20 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1.
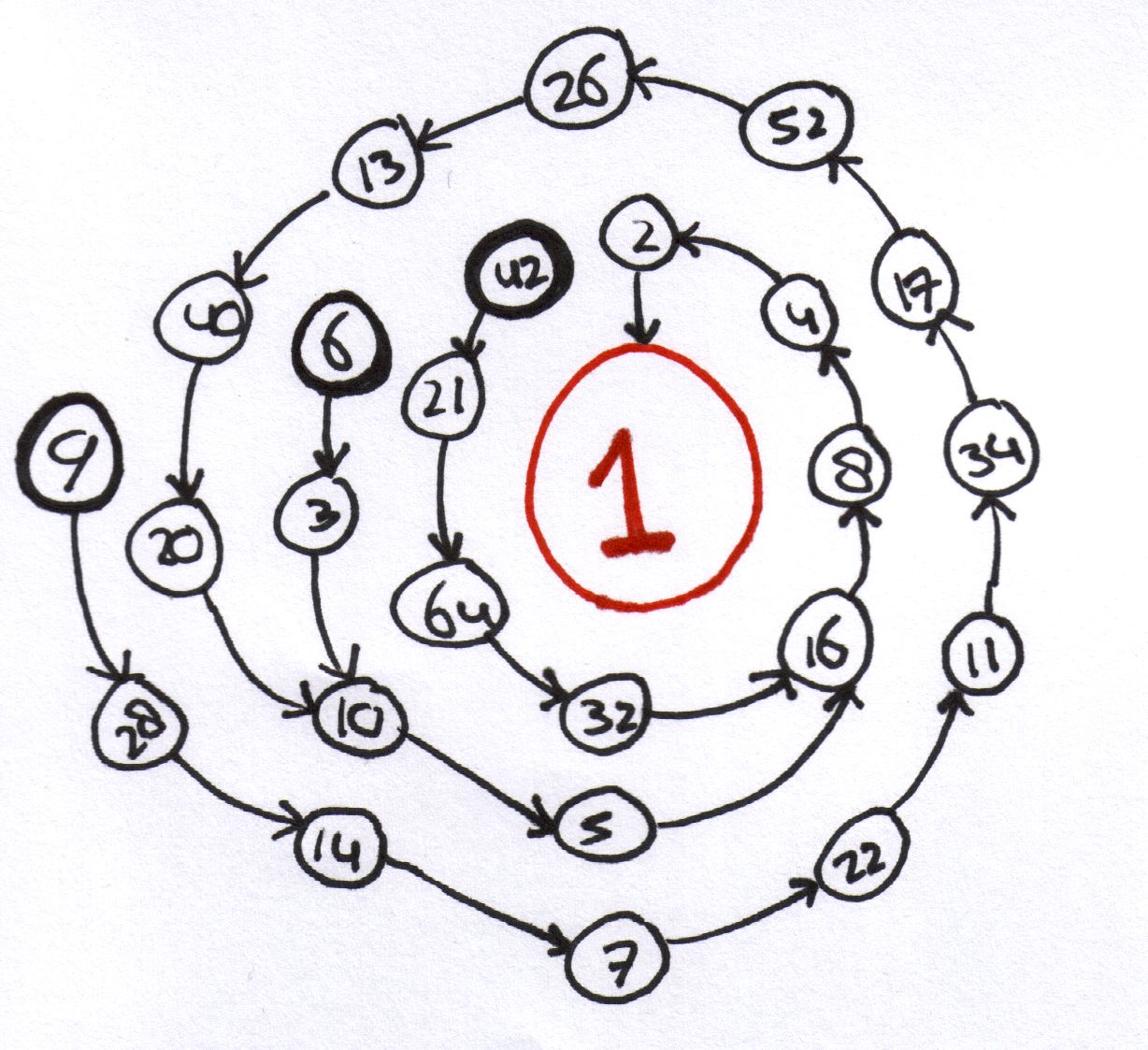
Het resultaat als je begint bij 6, 9 of 42.
Je stopt bij één, omdat je vanaf daar in een vicieuze cirkel belandt: één gaat immers naar vier en dan via twee weer terug naar één. Het vermoeden van Collatz is dat je altijd op één uitkomt, met welk getal je ook begint.
Probeer het zelf maar eens voor je lievelingsgetal. Als je getal kleiner is dan 10^18 dan kom je zeker op één uit, tot die grens is het vermoeden met de computer getest. Het aantal stappen kan behoorlijk groot worden: als je begint met een bescheiden 27 heb je bijvoorbeeld al 112 stappen nodig voor je bij 1 eindigt.
De meeste wiskundigen denken dat het vermoeden van Collatz waar is en dat je inderdaad voor elk getal bij één zult eindigen. Maar niemand heeft een bewijs. De in 1996 overleden wiskundige Paul Erdös verzuchtte volgens de overlevering dat de wiskunde nog niet klaar was voor dit soort moeilijke problemen. Voor de zekerheid loofde hij toch maar 500 dollar uit voor een oplossing. Die oplossing is er nog steeds niet.
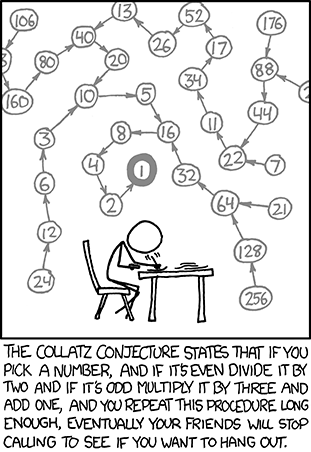
Dit alles vertelde ik op de borrel. De getallenvoorbeelden zocht ik snel op met mijn telefoon, iets wat ik ook van harte aanraad bij lastige vragen over Peloponnesische oorlogen. De vragensteller keek me wat teleurgesteld aan. Dus dit kunnen wiskundigen níet oplossen? Wat zitten jullie dan de hele dag achter jullie bureaus te doen? En wat kunnen jullie wel?
Het is misschien gênant om een vraag te krijgen over een onderwerp waarvan je nog nooit hebt gehoord. Maar het is nog veel gênanter om toe te moeten geven dat jij en je vakgenoten een ogenschijnlijk eenvoudig probleem niet kunnen oplossen.
 Internetbureau Rotterdam
Internetbureau Rotterdam 
