Wiskundemeisjes
Deze column verscheen afgelopen weekend in de Volkskrant. In de online versie van de vorige column waren de kansen waarnaar deze brief verwijst al verbeterd.
Beste Ionica,
Wekelijks lezen jij en je collega Jeanine Daems iemand de les die een wiskundig foutje maakt. Als wiskundemeisjes leggen jullie nog één keer uit hoe het wel moet. Als lezer verwacht ik daarom dat je zelf uiterst zorgvuldig bent in je redeneringen.
Vorige week besprak je de loting voor de kwartfinales van de Champions League. Die viel zo uit dat van de acht teams “de grote vier” in vier verschillende finales belandden. Je legde aan Johan Derksen uit wat de kans is op zo’n verdacht handige loting. Om dat uit te rekenen, geef jij bij de loting elk team een getal tussen de één en acht. In de eerste kwartfinale speelt team één tegen team twee, in de tweede team drie tegen team vier, enzovoorts. Vervolgens beweer je dat “de grote vier” elkaar ontlopen als ze allemaal een even nummer krijgen óf juist allemaal een oneven nummer. Daarna laat je het telwerk aan de lezer over en komt al handenwapperend op een kans van één op vijfendertig.
Alleen is het een beetje dom dat je vergeet dat de vier teams ook niet tegen elkaar spelen als ze bijvoorbeeld posities één, vier, vijf en zeven loten. En zo zijn er nog veel meer mogelijkheden. Om precies te zijn: acht keer zoveel. De juiste kans is dan ook acht op vijfendertig.
Jij nam je berekening over van een andere wiskundige, maar dat is natuurlijk geen excuus. Als je het altijd allemaal zo goed weet, dan mag je best even controleren of wel klopt wat je opschrijft. Ik zal nog één keer uitleggen hoe dat in dit geval had gekund. Als we beginnen met het eerste team, dan kan dat nog alle acht vrije nummers krijgen zonder dat het één van de andere “grote” teams tegenkomt. Voor het tweede grote team zijn er nog zeven plekken vrij en de kans is \(\) dat zij bij de loting het eerste team ontwijken. Het derde team heeft nog zes open plekken en op vier daarvan hoeven ze niet tegen de eerste twee teams te spelen. Tenslotte zijn er voor het vierde team nog vijf plekken over, waarvan twee plekken niet tegen de andere groten. Kortom: de kans op een loting waarbij de grote vier elkaar ontwijken is \(\).

Terug naar school, Ionica Smeets!
Alle andere kansen in je column kloppen door jouw fout ook niet. De kans op een loting zoals Johan Derksen hem beschreef is ruim elf procent. En als hij voor de loting de kans op doorgestoken kaart op vijfentwintig procent schatte, dan stijgt die kans na deze uitslag naar bijna vijfenzeventig procent. Graag gedaan hoor wiskundemeisje, het was een kleine moeite om het even goed uit te rekenen.
Het enige excuus dat je hebt, is dat kansrekenen notoir lastig is. Een onjuiste redenering klinkt vaak heel plausibel. Martin Gardner schreef eens dat er geen ander gebied van de wiskunde is waar experts zó makkelijk kunnen blunderen. Maar lieve Ionica, je mag voortaan best iets milder zijn voor anderen die eens een foutje maken met wiskunde. Wie zonder zonde is, enzovoorts. Misschien moet je eens wat kritischer naar jezelf kijken.
Groeten van jezelf,
Ionica
Deze column verscheen afgelopen weekend in de Volkskrant. Helaas zat in die column een fout, hieronder de gecorrigeerde versie.
Beste Johan Derksen,
Vorige week was natuurlijk een rare week voor u. Eerst liep u boos weg bij Voetbal International omdat uw collega Wilfred Genee weer eens iets stom zei. Maar de avond daarna zat u toch weer bij hem aan tafel, omdat u vastzit aan uw contract (en omdat u het natuurlijk heel erg leuk vindt om over voetbal te kletsen). U besprak toen de loting van de Champions League. Eerder die dag waren deze kwartfinales geloot: Malaga-Dortmund, Madrid-Galatasaray, PSG-Barcelona en Bayern-Juventus. Uw collega René van der Gijp vatte het als volgt samen: “Dit kan toch bijna niet waar zijn. De Spanjaarden ontlopen elkaar en de Duitsers ontlopen elkaar.” U voegde daar even later aan toe: “Dit riekt naar malversatie. Het is duidelijk dat Bayern en Barcelona verder moeten.”
De loting.
Er zijn verschillende dingen opmerkelijk aan deze loting: “de grote vier” (Madrid, Barcelona, Bayern en Dortmund) ontwijken elkaar en het derde Spaanse team Malaga speelt niet tegen andere Spanjaarden. Dat komt wel heel mooi uit voor een organisatie die zoveel mogelijk kijkers wil trekken. Zelfs Wilfred Genee had door dat dit merkwaardig was en noemde het oplichterij van de eerste orde. U mompelde instemmend: “Je kunt het nooit hardmaken, maar dit is te mooi voor woorden.”
Hardmaken is lastig, maar u kunt wel uitrekenen wat de kans op zo’n loting is. Voetballiefhebber en wiskundige Henk Tijms ging aan de slag (en tipte mij over dit onderwerp). De kans dat het eerste team van de grote vier geen van de andere drie treft is \(\). Voor het tweede team is die kans dan \(\) en voor het derde team \(\). Het vierde team zit dan automatisch goed. De totale kans op een loting waarbij de vier teams elkaar ontwijken is daarmee \(\). Nemen we ook nog de kans mee dat Malaga niet tegen een Spaans team uitkomt, dan is de kans op zo’n loting vier op vijfendertig, oftewel ruim elf procent. Dat is niet extreem klein. Zo’n loting is waarschijnlijker dan een tatoeage van Wilfred Genee omringd door hartjes op uw bovenarm.
Nu weet u dus wat de kans is dat de gegeven uitslag valt als de loting eerlijk was. Maar eigenlijk wilt u weten wat de kans is dat deze loting eerlijk is áls deze uitslag valt. Dat is een stuk lastiger. Om dat te berekenen moet u eigenlijk vóór de loting zeggen hoe groot u de kans acht dat er gesjoemeld wordt om te zorgen dat de wedstrijden precies zo uitkomen als hierboven. Na de uitslag kunt u dan de kans uitrekenen dat de loting eerlijk was. Zeg dat u voor de loting inschatte dat er vijfentwintig procent kans was op valsspelen. In dat geval stijgt met de gegeven lotingsuitslag de kans op doorgestoken kaart naar bijna vijfenzeventig procent- volgens u en de wiskunde. De complete berekening past helaas niet in deze brief, maar op deze manier kunt u misschien wel degelijk hardmaken dat de loting te mooi voor woorden is.
Dat de beste moge winnen,
Ionica
Deze column verscheen afgelopen weekend in de Volkskrant.
Hallo meisje van de telefoonwinkel,
Vorige week stond ik aan je balie. Mijn telefoon was die dag kapot gevallen en ik wilde zo snel mogelijk een nieuw toestel. Liefst de iPhone 5 die ik al een tijdje op het oog had. Mijn abonnement kon ik opzeggen en ik wilde best naar een andere aanbieder. Dus ik vroeg aan jou wat mijn beste optie was.
Je stelde me heel gericht een aantal vragen. Hoeveel belde ik per maand? Stuurde ik veel sms-jes? Zat ik vaak op internet? Daarna kwam je met een overzicht van allerlei abonnementen van verschillende aanbieders. Het was wat lastig om ze met elkaar te vergelijken, de één had iets meer belminuten, maar bij de ander belde je na tien minuten altijd gratis.
Nog lastiger was het om de prijzen te vergelijken. De aansluitkosten, de eigen bijdrage voor het toestel en de maandprijzen varieerden. Daarnaast liepen er ook nog allerlei verschillende kortingsacties. Het duizelde me van alle bedragen. En toen, meisje van de telefoonwinkel, deed jij iets heel slims. Voor zes verschillende opties rekende jij netjes uit wat ze me alles bij elkaar zouden kosten voor twee jaar. Al die abonnementen hadden immers dezelfde looptijd van twee jaar.
Je nam alle kosten mee: bellen, internet, toestel, nummerbehoud en wat er al niet meer bij hoorde. Na een kwartiertje rekenen concludeerde je welk abonnement voor mij het voordeligste was. Blij met jouw goede service sloot ik dat onmiddellijk af.

Daarna probeerde je me wel nog een verzekering aan te smeren. Je legde uit dat toestellen vaak vallen of gestolen worden. Voor slechts zestien euro per maand kon je me een verzekering aanbieden. Ik bedankte, die verzekering had ik niet nodig. Jij wees vriendelijk naar het kapotte toestel waarmee ik de winkel was binnengekomen. Ik wierp tegen dat ik dat toestel al meer dan drie jaar had; en dat de totale verzekeringspremie in drie jaar hoger was dan de kostprijs van het toestel. Jij gaf je gewonnen.
Tevreden verliet ik de winkel. Wat was ik toch slim, wat had ik een mooi nieuw toestel en dat met zo’n lekker voordelig abonnement. Tot ik ‘s avonds bedacht dat er nog een optie was die je helemaal niet genoemd had Want meisje van de telefoonwinkel, wat zou het kosten als ik het toestel los had gekocht en een sim-only abonnement nam voor bellen en internet? Ik sloeg aan het rekenen en ontdekte dat dit honderden euro’s goedkoper was. Waarom heb je me dat niet verteld? Krijg je soms minder commissie op dit soort abonnementen?
Ach meisje, het is natuurlijk niet jouw schuld. Jij deed gewoon je werk. En ik had niet zo dom moeten zijn om onvoorbereid naar je winkel te komen. Achteraf gezien had ik beter een dagje kunnen wachten en eerst zelf rustig op internet wat abonnementen vergelijken. Ik zit mijn abonnement tandenknarsend uit en over twee jaar zal ik mijn voorwerk beter doen. Reken er maar niet op dat ik nog aan je balie kom.
Tuut, tuut, tuut,
Ionica
Deze column verscheen zaterdag in de Volkskrant.
Beste wethouders van onderwijs van de Nederlandse gemeenten,
Er gaat iets niet helemaal goed met het onderwijsaanbod. In bepaalde regio’s zijn er op meerdere middelbare scholen veel meer aanmeldingen dan plaatsen. Dat probleem speelt breder dan de gewilde gymnasia in Amsterdam: ook op vmbo- en havo-afdelingen, ook in andere regio’s. En dan moet er geloot worden.

Ik was niet echt bekend met het lotingssysteem, maar een collega vertelde me laatst over de schoolkeuze van zijn dochter, en dat verbaasde me nogal.
Hij gaat zijn dochter namelijk niet aanmelden voor de school van haar eerste keus. Het werkt in regio Utrecht als volgt: bij je eerste keus loot je mee. Wie dan wordt uitgeloot, kan bij zijn tweede keus alleen nog terecht als die school niet inmiddels vol zit met kinderen die die school als eerste keus hadden. Daarna zijn er dus al twee plaatsingsrondes voorbij en bestaat de kans dat alle andere leuke scholen ook vol zijn. Dat is erg zuur als je volop open dagen hebt bezocht, doordacht hebt gekozen en je vriendinnen wel ingeloot zijn.
Daarom schrijft mijn collega zijn dochter meteen in voor haar tweede keus: ze heeft daar nu veel kans, maar als ze zich voor haar eerste keus inschrijft en uitgeloot wordt (die kans is groot), kan ze er waarschijnlijk niet meer terecht.
Een systeem waarbij mensen expres hun eerste keus verzwijgen, vindt u dat niet gek? Een lotingssysteem zou toch moeten voldoen aan de eis dat als je eerlijk zegt wat je het liefste wilt, dat je er dan in ieder geval niet op achteruit gaat? Waarom kiest u niet voor een beter systeem?
Ik las deze week in het Parool dat daar nu wel onderzoek naar gedaan wordt. Op de UvA en de VU proberen economen algoritmes van Nobelprijswinnaars Alvin Roth en Lloyd Shapley toe te passen op het Nederlandse lotingsprobleem.
Deze algoritmes zijn koppelprocedures die verschillende aanbod- en afwijsrondes doorlopen. Bijvoorbeeld: stagiairs moeten aan instituten gekoppeld worden, een-op-een. Zowel de instituten als de stagiairs hebben een top-zoveel gemaakt van acceptabele kandidaten dan wel instituten. Vervolgens doet elk instituut een stagiair een aanbod. De crux zit hem hierin: de stagiairs nemen het beste aanbod nog niet definitief aan, maar ze wijzen de slechtere wel af. Die doen vervolgens opnieuw een aanbod aan de volgende stagiair op hun lijst. Enzovoorts. Op het moment dat geen enkel instituut meer afgewezen wordt of geen enkel afgewezen instituut een nieuw aanbod wil doen, accepteren de stagiairs tegelijk elk hun beste aanbod. De instituten die nog geen stagiair hebben, gaan een volgende ronde in.
Roth heeft een soortgelijk maar ingewikkelder koppelalgoritme toegepast op schoolkeuze in New York (wat natuurlijk geen een-op-een-koppeling is). Voordelen: minder leerlingen komen op een school terecht die niet op hun lijstje stond, en strategisch lijstjes maken, zoals mijn collega doet, heeft geen zin.
Of zo’n algoritme inderdaad ook in uw geval werkt, is nog even afwachten, maar houd het in de gaten! Want een betere procedure bedenken dan nu, dat bent u aan uw jeugd verplicht.
Met verwachtingsvolle groeten,
Jeanine
Deze column verscheen afgelopen weekend in de Volkskrant.
Beste Tooske, Valerio, Britt en al die andere BN-ers die nog niet meededen aan Wie is de mol,
Na de bloedstollende finale van afgelopen donderdag hopen jullie natuurlijk dat jullie volgend seizoen gevraagd worden voor Wie is de mol. Terecht hoor! Daarom schrijf ik jullie nu maar vast. Het valt me namelijk op dat de kandidaten elk jaar dingen doen die niet zo slim zijn. En dan bedoel ik niet de onhandige acties waardoor een opdracht mislukt, zodat iedereen zich afvraagt of diegene misschien de mol is. Nee, ik bedoel acties die nogal onhandig zijn voor de kandidaat zelf. Daarom hierbij een tip voor een opdracht die vrijwel elk seizoen in één of andere vorm voorbij komt.
Eén kandidaat staat bovenop een enorme toren, wankele brug of ander doodeng hoog bouwwerk. De vraag is of de waaghals naar beneden durft te springen, abseilen, of wat de programmamakers dat jaar weer verzonnen. Een andere kandidaat staat lekker beneden en moet voorspellen of degene bovenaan het durft. Als de gokker het fout heeft, dan wint de ander jokers of iets anders gaafs.
Als jij op die toren staat, moet je bedenken wat de ander denkt dat jij doet. En dát moet je dan niet doen. Tenzij je bedenkt dat de ander bedenkt dat jij bedenkt wat hij bedenkt en dan stiekem de andere optie kiest. Het gevaar van zover doordenken is alleen dat je al snel in een oneindige spiraal belandt en helemaal geen tijd meer hebt om te springen. Hiervoor is er wiskundig gezien een prima oplossing. Gooi een muntje op. Kop is springen. Munt is niet springen. Zo ben je volkomen onvoorspelbaar en heb je zonder zenuwslopend denkwerk vijftig procent kans op de jokers. Een nadeel van deze strategie is trouwens dat hij iets minder goed werkt voor mensen met hoogtevrees.
In navolging van de recensiekoning een filmpje van Kees Tol, gewoon omdat het kan.
Dan nog een voorbeeld van een onhandige actie uit een eerder seizoen. Bij deze opdracht stond je als kandidaat tegenover een tegenstander. Je kreeg vragen die je eerder in het programma ook al had beantwoord. Nu moest je kiezen of de ander jouw antwoorden mocht horen. Je kon bij elke vraag liegen, maar dan zei de presentator wel dat je een verkeerd antwoord gaf. Bij drie foute antwoorden mocht je tegenstander lezen in jouw geheime aantekeningenboekje. Je moest je leugens dus strategisch inzetten. Bij een vraag als “Wie is volgens jou de mol?” kon je mooi een verkeerde naam noemen. Daarna wist de ander alleen wie je níet verdacht. Maar de presentator stelde ook vragen waarop maar twee antwoorden mogelijk waren, bijvoorbeeld “Spreekt de mol Spaans?”. Liegen daarop had natuurlijk geen enkele zin. Zodra de ander wist dat je loog, begreep hij ook wat je echte antwoord was. Toch loog destijds een groot deel van de kandidaten bij dit soort tweekeuzevragen. Waren ze hun eigen antwoorden vergeten? Of wilden ze zo de indruk wekken dat ze het spel niet goed begrepen, zodat de tegenstander hen zou onderschatten? Of wilden ze soms de indruk wekken dat ze de indruk wilden wekken enzovoorts?
Verwarde groet,
Ionica
Beste Albert Heijn,
Het was me gelukt om jullie superdieren en voetbalplaatjes buiten de deur te houden, maar nu hebben jullie me te pakken. Jullie keukenmini’s zijn onweerstaanbaar! Mijn zoon heeft een schattig speelkeukentje en ik wil het liefste zijn plankjes vol zetten met kleine flesjes olijfolie, zakjes penne en al die andere mini’s. Jullie delen maar liefst vijftig verschillende uit, dus ik ben flink aan het sparen.
Bij elke vijftien euro aan boodschappen krijg je een gratis keukenmini. Om de complete set van vijftig te verzamelen moet je dus voor zevenhonderdvijftig euro aan boodschappen doen. En dat alles binnen de zes weken dat de spaaractie loopt. Zoveel geld geef ik normaal niet uit bij de supermarkt.
Bovendien ben je alleen voor zevenhonderdvijftig euro klaar als je nooit dubbele mini’s krijgt. Die kans is helaas nogal klein. Als jullie kassameisjes de keukenmini’s volkomen willekeurig uitdelen, dan is de kans dat je achter elkaar vijftig verschillende krijgt ongeveer één op een triljard. Dat is net zo waarschijnlijk als dat ik een zandkorrel ergens op aarde in gedachte neem en dat jullie dan raden welke zandkorrel dat precies is.
Zelf kreeg ik toe nu toe al flink wat dubbele. Op de een of andere manier krijg ik bij de kassa steeds weer visjes en maïskolfjes. Nu houd ik erg van vis en maïs, maar ik wil ook dolgraag die kleine wortel, dat spiegeleitje en die mini-deegroller.
Hoeveel boodschappen moet ik naar verwachting doen om alle vijftig mini’s te sparen? Zodra je één mini hebt, wil je die ene niet meer krijgen. De andere negenveertig zijn goed en je moet gemiddeld 50/49 mini’s krijgen om een goede te hebben. Zo reken je verder tot je bijna klaar bent. Als je al negenveertig verschillende mini’s hebt staan (hoera!), dan wacht je op die ene. De kans dat je die krijgt is één op vijftig en je zult gemiddeld vijftig willekeurige mini’s moeten verzamelen om die ene ontbrekende te pakken te krijgen. In totaal moet je gemiddeld 225 mini’s krijgen voor je een complete set van vijftig verschillende hebt. Dan moet je dus voor 3375 euro aan boodschappen doen. In zes weken. Oftewel: “Hamsteren!” zoals jullie in de reclame graag roepen.
Mijn collega Tammo Jan Dijkema berekende een paar jaar geleden dat het met jullie voetbalplaatjes ook al zo’n ellende was. Toen moest de argeloze spaarder gemiddeld 331 pakjes voetbalplaatjes verzamelen om de complete set van 270 voetballers te voltooien. Interessant genoeg kreeg je zo’n pakje bij elke tien euro aan boodschappen. Destijds moest je dus voor 3310 euro aan boodschappen doen. Streven jullie soms bij al deze acties naar minstens 3300 euro aan boodschappen per klant?
Eigenlijk zit er maar één ding op, ruilen met andere noeste spaarders. Of wacht, er is nog een oplossing. In de speelgoedwinkel zag ik een set van vijftig keukenmini’s voor een tientje. Dat kan ik makkelijk betalen met het geld dat ik uitspaar door bij een goedkopere supermarkt boodschappen te halen.
Zuinige groet,
Ionica
Deze column verscheen afgelopen zaterdag in de Volkskrant.
Beste Alice Amos,
Je bent pas drie. Toch schrijf ik je deze brief. Dat zou ik bij een gemiddelde 3-jarige niet in mijn hoofd halen, natuurlijk, maar jij bent dan ook heel bijzonder. Het is jammer dat deze krant in het Nederlands verschijnt, want dat beheers je geloof ik nog niet, maar er is vast iemand in de buurt die je wil helpen. Twee talen spreek je al vloeiend, Russisch en Engels, dat beetje Nederlands pik je vast ook snel op.
Want: je leert snel en je kunt al veel. Je bent vorige week dan ook toegelaten tot de Britse tak van Mensa, de vereniging voor hoogbegaafden. Je IQ is maar liefst 162. Heel erg hoog! Maar wat zegt zo’n getal?

Het gemiddelde IQ is 100, per definitie, en IQ is normaal verdeeld. Je weet misschien al wel wat dat betekent: de verdeling van IQ’s over mensen van dezelfde leeftijdsklasse heeft de vorm van een klok. Die klokvorm kom je ook tegen als je in een grote groep even oude meisjes gaat tellen hoe vaak elke lengte voorkomt en daar een grafiek van maakt, bijvoorbeeld.
De IQ-kromme is het hoogst bij 100, en de extremen worden steeds onwaarschijnlijker. Twee procent van de bevolking zit boven de Mensa-grens van 130, en jij behoort tot de twee op de honderdduizend mensen die een IQ hebben van 162 of meer.
Zo’n hoog IQ is trouwens lastig te meten, veel tests gaan zo ver niet. Het precieze getal zou ik dus met een korrel zout nemen als ik jou was. Het is sowieso wat omstreden wat een IQ precies betekent. Intelligentie is breder dan een IQ-test kan meten. Die 162 is vooral een pragmatische indicatie van hoe jouw cognitieve vaardigheden zich verhouden tot die van leeftijdsgenoten. (Ja, moeilijke woorden, daar houd je vast wel van!)
Het is fijn dat je nu bij Mensa kinderen tegenkomt die jou begrijpen, die om je grapjes lachen, die af en toe van je zullen winnen met een spelletje. Want als je zo uitzonderlijk slim bent, kun je je heel eenzaam voelen. Maar wat me helemaal niet fijn lijkt: je naam en IQ staan nu overal verspreid op internet. Je hele leven zal je IQ op 3-jarige leeftijd opduiken als iemand je googlet! Je wordt slimmer dan Einstein genoemd! Wat een druk op zo’n klein meisje! Waarom hebben je ouders daar in hemelsnaam mee ingestemd?
Ik gun je mensen om je heen die je actief aanmoedigen om dingen te proberen die je niet vanzelf al kunt. Die je leren dat het juist extra leuk is om iets te leren als het moeite heeft gekost, dat je dan echt trots op jezelf kunt zijn. Dat het helemaal niet erg is om fouten te maken. Dat je niet wordt uitgelachen als je een keer niet het beste cijfer haalt. Dat je passies vindt die het waard zijn om je best voor te doen. Want als dat allemaal lukt, dan word je misschien wel echt een nieuwe Einstein! En: blij met wie je bent, hoe bijzonder dat ook is.
Alle goeds,
Jeanine
Deze column verscheen afgelopen zaterdag in de Volkskrant.
Lieve Rekentoets,
Wat houd ik van je vragende blik, je uitdaging, je aspiraties! Van je niveau, je sprankelende beloftes! Ik verheug me al op onze verdere kennismaking! Die laat echter wat langer op zich wachten dan gehoopt…
Ik heb je in mijn eigen schooltijd nooit gezien. Ik was dus enigszins gespannen toen ik je onlangs voor het eerst ontmoette. Want wat zou je precies inhouden? Was je niet te hoog gegrepen? Was je in het echt wel zo mooi als ik me had voorgesteld?

Je bent in het leven geroepen omdat we tot de top vijf van de wereld willen gaan behoren. Want, zo weten we allemaal, het beste middel om zeker te weten dat er iets geleerd wordt, is een prachtige toets als jij! Was het maar zo makkelijk. O lieve rekentoets, je zou het allemaal komen oplossen, als de langverwachte prins op het witte paard! Door jouw komst zouden alle leerlingen als bij toverslag boven zichzelf uitstijgen!
Mijn leerlingen kunnen heus wel rekenen, ze zijn niet voor niets op havo of vwo beland, meestal dankzij je bekendere broertje cito-eindtoets. Maar jij eist meer! Dat betekent dat niet alleen, zoals wel eens gedacht wordt, het rekenniveau van eind groep 8 behouden moet blijven, nee, daar moet echt wat bij. Terecht!
Nu ben je echter, bleek een maand of wat geleden, twee jaar uitgesteld. Dat is gelukkig niet helemaal waar, mijn leerlingen gaan je komende maand gewoon maken, onze date staat al in mijn agenda! “Uitgesteld” betekent: je komt volgend jaar wel op de eindlijst terecht, maar dan zonder consequenties. Je telt nog even niet mee voor slagen of zakken.
Want: je was te moeilijk. Of eigenlijk: je was niet te moeilijk, de wereld is gewoon nog niet klaar voor jou! Je bent je tijd vooruit. Veel leerlingen bereiken jouw niveau niet vanzelf (72% van de havisten en 32% van de vwo’ers scoren onvoldoende). Nou, verrassend! Als rekenen altijd al voldoende in het wiskundecurriculum had gezeten om het beoogde niveau te bereiken, dan was jij helemaal niet nodig geweest. Maar: “Rekenen betreft een relatief nieuw te toetsen inhoud in het voortgezet onderwijs”, schrijft het ministerie.
Je bent dus onmisbaar! Aan de andere kant komen er nauwelijks extra lessen: die rekenvaardigheid moet langs gaan komen in de wiskundeles en bij voorkeur bij andere vakken ook. Weinig extra investeringen dus, wel mooiere resultaten. En dat allemaal dankzij jou!
Het ministerie gedraagt zich in dezen een beetje als een slechte docent. Ga maar na: het deelt een taak uit, stelt een deadline, maar biedt niet voldoende ondersteuning (te weinig tijd, geld, niet optimaal werkende computerprogramma’s). Met als logisch gevolg dat er massaal onvoldoendes vallen, scholen zijn er nog niet klaar voor. En wat doet een slechte docent in zo’n geval, omdat hij zich schuldig voelt en de klagende ouders al ziet aankomen: de toets maar niet meetellen. Dan zeurt er voorlopig niemand meer over de wat gehaaste voorbereiding.
Maar, lieve rekentoets, dat is dus niet jouw schuld. En ik blijf intussen smachtend uitkijken naar de vele lange avonden die we samen zullen door gaan brengen!
Je liefhebbende Jeanine
Deze column verscheen afgelopen weekend in de Volkskrant.
Beste ING,
Elke keer dat ik bij een van jullie geldautomaten pin, verschijnt er een of andere koddige boodschap op het schermpje. Zo leerde ik dat je tegenwoordig bij steeds meer winkels kunt betalen met je pinpas. Goed dat jullie dat even zeggen, want ik had werkelijk geen idee! Die moderne tijden gaan ook maar door.
Deze week kreeg ik ineens een ander berichtje: “Ontvang vijf euro per 2.500 saldogroei.” Thuis zocht ik onmiddellijk meer informatie op over deze actie. Ik heb op dit moment geen spaarrekening bij de ING en dit zou een goede reden zijn om er één te openen. De actievoorwaarden bleken niet zo ingewikkeld: jullie kijken naar het totale spaarsaldo van een klant op 2 januari en 14 april. Voor elke 2.500 euro die er in die tijd is bijgekomen, krijgt de nijvere spaarder van de ING vijf euro (met een maximum van vijfhonderd euro). Wie net als ik nog geen spaarrekening bij jullie heeft, kan zich tot 3 maart nog aanmelden. Volgens jullie vriendelijke klantenservice telde in dat geval de eerste storting op de nieuwe spaarrekening als startsaldo voor de actie.
Klik op het plaatje voor een vergroting.
Voor ik enthousiast mijn nieuwe ING-spaarrekening aanvroeg, sloeg ik even aan het rekenen. Op zich is vijf euro per 2.500 euro niet heel erg veel, het is een schamele 0,2 procent. Al komt die bonus wel bovenop de gewone spaarrente. Maar helaas, beste ING, is de spaarrente bij jullie niet zo heel hoog. Bij jullie comfortrekening is de rente 1,6 procent. Als ik meer rente wil, dan moet ik een flinke minimuminleg hebben, of zorgen dat ik een bonusrente krijg voor mijn spaargedrag. Mijn huidige spaarrekening bij één van jullie concurrenten geeft zonder minimuminleg of ingewikkelde voorwaarden een rente van 2,2 procent (en ik zag dat er zelfs nog betere alternatieven zijn).
Als ik 2.500 euro op jullie comfortrekening zet, krijg ik per jaar veertig euro rente. Bij de concurrent is dat vijfenvijftig euro. Dus jullie rekening is minder gunstig, zelfs met die eenmalige spaarbonus van vijf euro. Hoewel...die bonus krijg je ook als het geld maar een heel korte tijd op een ING spaarrekening staat. Het gaat immers alleen om de groei van je saldo.
Daarom hebben jullie me toch overtuigd dat het een goed idee is om bij jullie een spaarrekening te openen. Dat ga ik deze week doen, ik zal er een klein symbolisch bedrag op storten. Vervolgens doe ik niets tot in april de actie bijna afloopt. Dan boek ik mijn complete spaargeld over naar mijn ING-spaarrekening. Na de einddatum van de actie gaat het geld snel weer terug naar mijn spaarrekening bij de concurrent met die hoge rente.
Voor elke 2.500 euro spaargeld die ik heb, krijg ik dus vijf euro van jullie. Hoera! Die spaarbonus verschijnt in april vanzelf op mijn gewone betaalrekening. Daar ga ik iets leuks van kopen. Het schijnt namelijk dat je met je pinpas in steeds meer winkels kunt betalen.
Bedankt voor de tip,
Ionica
Deze column verscheen afgelopen weekend in de Volkskrant.
Beste Republikeinen,
Deze week begon Barack Obama officieel aan zijn tweede termijn in het Witte Huis. Dat is natuurlijk balen voor jullie. Hoe kan het dat die linkse hippie alweer heeft gewonnen? Is er soms iets mis met het Amerikaanse verkiezingssysteem? Vorige week opperde jullie voorzitter Reince Priebus in elk geval om eens een andere manier van stemmen te overwegen. Een heel goed idee, want dat systeem met kiesmannen is op zijn zachtst gezegd merkwaardig.
Iedere volwassen Amerikaan mag op zijn favoriete presidentskandidaat stemmen. De stemmen worden vervolgens per staat geteld. Dat is allemaal nog goed te volgen. Maar dan komen die mysterieuze kiesmannen. Elke staat heeft een aantal van die kiesmannen: hoe meer inwoners, hoe meer kiesmannen. Per staat krijgt de kandidaat met de meeste stemmen alle kiesmannen van die staat. Bij de vorige verkiezingen haalde Obama in Florida bijvoorbeeld een krappe meerderheid van 50,01 procent, maar pikte daarmee alle 29 kiesmannen in. In totaal zijn er 538 kiesmannen te verdelen en degene die er de meeste krijgt, wordt de president. (Ik weet dat er wat uitzonderingen zijn, maar zolang de meesten van jullie geloven dat Nederland een stad in Denemarken is, denk ik dat we daar niet over moeten zeuren.)
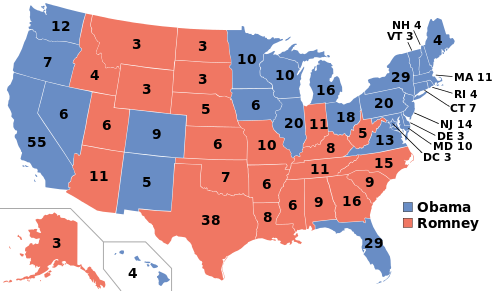
De kiesmannen per staat en naar wie ze gingen bij de verkiezingen van 2012.
Jullie partij suggereerde vorige week dat het beter zou zijn om de kiesmannen voortaan per district te verdelen in plaats van ze allemaal aan de winnaar van de hele staat te geven. Jullie noemden als voorbeeld Michigan, een staat die in hart en nieren Republikeins is. Bij de verkiezingen won Romney er in negen van de veertien districten. Desondanks ging alle kiesmannen naar die verdraaide Obama.
Die kiesmannen vertekenen inderdaad de uitslag en jullie voorstel om ze anders te verdelen, is helemaal niet zo gek. Het is alleen een beetje jammer dat jullie alleen een ander stelsel willen invoeren in de staten waar dat voor de Republikeinen gunstig is. Dat is niet zo netjes.
Daarnaast is het een heel gedoe om de kiesmannen netjes over de districten te verdelen. Zou het niet veel makkelijker zijn om in elke staat de kiesmannen procentueel te verdelen? Als een kandidaat vijftig procent van de stemmen krijgt, dan krijgt hij ook de helft van de kiesmannen. Bij het optellen van de uitslagen moet je eventueel een beetje afronden, maar dat is allemaal niet zo ingewikkeld. Ik heb even gerekend aan de uitslag van vorig jaar: met dit systeem zou Mitt Romney 256 kiesmannen hebben gekregen. Vijftig meer dan hij er nu had, maar helaas voor jullie nog niet genoeg voor de meerderheid.
Nog makkelijker zou het zijn als jullie die kiesmannen er helemaal uitgooien. Het is misschien een naïef Europees idee, maar waarom doen jullie niet gewoon “meeste stemmen gelden?”. Al snap ik wel dat jullie als Republikeinen daar niet zo voor zijn, want in 2000 haalde George Bush minder stemmen dan tegenstander Al Gore, maar dankzij jullie gekke kiesmannensysteem werd hij lekker toch president.
Eigenlijk denk ik dat er maar één systeem is dat de Republikeinen altijd een groot voordeel geeft. Stel voor om de kiesmannen te verdelen volgens de grootte per staat, los van het aantal inwoners. Dan zitten jullie goed. Ik ben alleen bang dat dit voorstel nog meer hoongelach op zal leveren dan jullie huidige ideetje.
Best wishes,
Ionica
 Internetbureau Rotterdam
Internetbureau Rotterdam 

